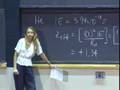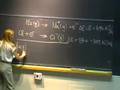Lecture 23: Cell Potentials and Free Energy

Related Resources

Cell Potentials and Free Energy (PDF)

• Download English-US transcript (PDF)

The following content is provided by MIT OpenCourseWare under a Creative Commons license.

Additional information about our license and MIT OpenCourseWare in general is available at ocw.mit.edu.

Today I will begin by talking about a subject that we were just getting to at the end of class last time, and that will be electrolysis. And this is an interesting topic. One of the examples of electrolysis that is commonly used is that which forms the basis for the so-called Dow process.

Here, what I am representing is a container.

And a container that would be used to house molten magnesium chloride. If you take magnesium chloride, which is a typical salt, and get it hot enough, then it will become liquid. And when it becomes liquid in the melt, what you can do is carry out a non-spontaneous reaction by applying an external voltage.

So, the idea is that this is some source of a potential difference. And you can take a positive electrode and a negative electrode and immerse it into the melt. And if the potential is sufficiently great, you can force a non-spontaneous reaction to run, because overall, the reaction will be spontaneous when you factor in the potential difference of the external source.

And, in this particular case, the reaction that would be taking place is as follows. At one side we would have magnesium two plus ions being reduced to, at this temperature, liquid elemental magnesium.

So, metallic magnesium at one electrode.

And, at the same time, at the other electrode, what would be taking place is the oxidation of chloride ions, two of which counterbalance the magnesium two plus in the salt magnesium dichloride.

And we put in a couple of electrons.

Sorry, we are oxidizing chloride to Cl two, which would be bubbling out as a gas at the temperatures of this melt. You initially would have this molten salt. You would immerse your two electrodes. You would apply an external potential. And if that potential is great enough, then these two reactions start taking place at the two electrodes. And you can see that in order for this to happen, chloride is being oxidized.

And so we can see then that this must be the source of the positive electrode and electrons will be going this way and going down here. And when they collect in this electrode on the left, they are used to reduce magnesium two plus to liquid magnesium.

So, that is an electrolysis reaction in which something that does not want to happen, namely the reduction of magnesium two plus to magnesium zero by chloride ions, that is non-spontaneous. And we are forcing it to happen by applying this external potential.

And just how great must that external potential be?

Well, Christine, could you locate for me on the table, there, the potential for magnesium two plus plus two electrons going to magnesium and the potential for Cl two plus two electrons going to two Cl minus?

Note that our standard potentials that we defined last time, relative to the standard hydrogen electrode, are always written as reduction potentials by convention.

What is it here? Can we zoom in on it?

Zoom in our finger.

Okay. By the way, I had her do this in part because I wanted to draw your attention to this table that is in one of the appendices of the textbook.

So, it is in the back. There is an abbreviated form of this table right in Chapter 12, which you should be reading.

But when you want to find a standard potential that is not in that abbreviated table, you will now know that you can go to your appendix to find that reduction potential.

Christine, please read out to me the value for the chloride.

Is that the one that you have there?

+1.36. Okay.

And this is positive of the standard hydrogen electrode, showing you that Cl two is an oxidizing substance.

And then what about the magnesium plus two electrons? -2.36.

Remember I mentioned last time that elemental sodium was around -2.7 volts, so it was a very strong reducing agent, magnesium. It is also a very strong reducing agent. Chlorine is an oxidant, so clearly the direction of spontaneity in this system is for a magnesium metal to be reducing Cl two to make chloride ions. And that is why the form of the salt that Henry Dow as a young man was extracting from the briny marshes near his home in Michigan, and later founded the Dow company on the basis of chemistries like this.

That is how you found it, as magnesium two plus, 2 Cl minus. And so, overall, if you reverse the sign of the anode reaction and add it to the cathode reaction, you are going to see that this one is downhill, sorry, is non-spontaneous by an absolute magnitude of 3.72 volts, which is the difference between these two values, this absolute difference in potential. That means that we are going to have to apply an external voltage of greater than 3.72 volts, positive, in order to get this thing to run and to be able to get gaseous Cl two bubbling out and in order to get liquid molten magnesium to be formed and separating from the molten magnesium chloride.

That is a large external potential.

That is the price that you have to pay to make this non-spontaneous reaction go. And that is the minimum price.

If we could just briefly switch to the Athena from the document camera. I want to mention this one word, overpotential.

You will see an explicit definition of the word overpotential given in my notes and in your book, but what overpotential is, in fact, a number.

And it is the amount of voltage that is greater than this non-spontaneous cell potential that you have to apply in order for the reaction really to start kicking in and working.

In practice, you choose maybe a couple platinum electrodes, and you dip them into the thing that you want to electrolyze, and you apply an external potential. And, in practice, that external potential is something much greater than the cell voltage of interest. And sometimes it is even a large amount in excess. And the reason has to do with the barrier to the reaction, that is introduced by the way that it takes place at the interface on the surface of these electrodes, so you have to apply some overpotential. That is energy that you have to put into the system over and above the inherent energy of the electrolysis to make it actually work in practice.

And so, the substance that we would most like to be able to electrolyze is water. Because, if you think about it, electrolysis of water would produce hydrogen and oxygen.

And then we could have those in our fuel tank, and we can go ahead and let combustion take place, which produces what? It would produce water.

You would get a beautiful complete cycle, if you could do a good job of electrolyzing water into its components, H two and O two.

And the reason that that is difficult is because you have to put in energy, somehow, in order to make that non-spontaneous reaction go uphill.

We would like to make that the basis for the hydrogen economy.

I really love Iceland. This is my favorite country, I think. Although, I have never been there. And it is, because they do this reaction. They do this electrolysis of water every night, so that they will have hydrogen and oxygen for combustion purposes the next day in their buses in the city. And they are actually doing this. And why are they able to do that? Well, their special location on the planet gives them a lot of free electricity that they can use to run the electrolysis of water to make hydrogen and oxygen every night. And then they can combust that in their buses. And you essentially have free hydrogen, and it is not a problem.

And in places like Iceland or other places in the world, where you have freely available energy from geothermal sources or from hydroelectric power, then you can do that.

You can use that energy, that electricity that is free, that the earth is just giving you, to go ahead and carry out the electrolysis of water and make hydrogen that way.

And we would like to be able to do that using photochemistry.

One possible way to get the positive holes in the electrons apart is to use h nu. A photon can impinge on a material and lead to the separation of charge in what is called a photovoltaic device. And, if you can interface a photovoltaic device to a couple of electrodes that have surfaces that are appropriate, chemically, for minimizing the overpotential, then you can use light coming in from the sun to make electrolysis of water happen to get hydrogen and oxygen from light that is coming in incident on the earth. And so, one thing that is currently ongoing research in a partnership at Caltech and MIT, and I am involved with this, this is Professor Nocera, here. And you will see this furry face walking around the hallways at MIT.

And he is an amazing guy. And if he does what he is trying to do right, he is probably going to be the next one in our department to win the Nobel Prize.

So, Professor Nocera is currently the professor of chemistry and professor of energy here at MIT.

He is the energy professor. And he is a lot more voluble and vigorous, I think, than I am.

He is really bouncing off the walls with energy.

And that is good because the technical challenges that we have to surmount in order to be able to use sunlight to carry out water oxidation, water electrolysis are very great, but they come down to chemistry and to molecules.

And starting on Wednesday, we are going to enter a part of the semester in which we treat the subject of bonding in chemistry in quite a bit of detail.

We are going to be talking about molecular orbitals and things like that. And if you get a good understanding of molecular orbital theory and electronic structure and the shapes of molecules, you may be able to contribute to this problem by helping to design molecules that can go on the surface of the electrodes.

And the purpose of those molecules is to reduce the overpotential for water electrolysis with sunlight as the source of the electrons and the holes.

And this man's entire life is defined by one number, and that is the overpotential. We are making electrode molecules that will bring down the overpotential and give us a free source of clean energy from water.

One week from today, you are going to have a little introduction to undergraduate research here at MIT.

We are going to have some visitors who will come in and talk to you about the 5 subject that is given during IAP. And the people who successfully complete the 5.301 subject are then guaranteed a position in a research laboratory in chemistry as an undergraduate research opportunities program student. If you want to get involved in the molecular chemistry of renewable energy, then you might want to make sure you are here on time for class on Monday, and you will get that introduction. And you can think about what to do in terms of 5.301. Now, I want to bring you up to speed on some more important concepts that pertain to electrochemistry. Let's talk about electrical work.

Here, I want to make an analogy to the way that electrons can do work when they fall through a potential difference and experience a potential difference.

I want to make an analogy between that and the way that things go downhill by virtue of the force of gravity.

And so, you can think of a waterfall of electrons flowing from a place of high potential to a place of low potential if you want to get an idea for our expression for the way that the free energy of reaction is related to electrical work.

And it is the total charge that is passed multiplied by the potential difference through which the charge is passing.

We have been talking about this potential difference and calling it E. And if it is standard potential, then we will use the superscript zero, or the little degree symbol for a standard.

And now, we want to know what is the total charge?

It is going to be negative n times the charge on the electron times N sub A, which is Avogadro's number.

And we are going to be interested in getting the total charge expressed in terms of a quantity per mole.

Actually, we are going to express it in Coulombs per mole.

And so, we combine e and (N)A together.

And this is one of our fundamental constants.

This is Faraday's constant. And you will remember that that is approximately 96,485.3 Coulombs per mole.

That is Faraday's constant. And we will use that as our way of expressing charge here. And so, we get the important expression, delta Gr is equal to negative nFE.

And we will use that a couple of times today in getting access to other quantities.

And what is n? That is going to be the stoichiometric number of electrons passed in the half-reaction of interest. I will show you a couple of examples of how you figure out what n is in this expression.

So, it is the total charge times the potential difference.

One of the things that this is useful for is for finding a relationship between an equilibrium constant and a standard cell potential. And we can do that by recalling from chemical equilibrium the expression that delta G is equal to minus RT ln K.

And now we have a new expression, down here, for delta G. And let's go ahead and insert that, and we will see that nFE is going to be equal to RT ln K.

And so, we can just rearrange that and solve for quantity of interest here. We are going to see that the equilibrium constant, K, is equal to an exponential of nFE divided by RT. And this should be for a standard potential.

And then this is the equilibrium constant, that special value of Q that applies when the system is at equilibrium. So, let me put the little superscript up here to make it clear that we are talking here about a standard potential. The idea is then if you have a reaction and you can express it in terms of half-reactions, then you can go to our table in the appendix, if those half-reactions happen to be in the table.

And then you can calculate the value of the standard potential for the cell that would be comprised of those two half-reactions, as we described last time.

And then, given these other quantities, we can calculate the equilibrium constant for the reaction.

So, it is a useful thing to be able to do.

You take a standard cell potential and then take a temperature like the standard temperature, 298.15K.

And you have your value of F that I gave you.

And you can look up, of course, the value for the gas constant. And you have n, from the stoichiometry of the number of electrons passing through this potential difference.

And then you can get K. And you see that this equilibrium constant K goes up exponentially as the standard cell potential increases. That is quite an interesting relationship, too.

And I would like to give you an example of how we can use this.

Let's consider a possible reaction of this sort.

This reaction, of course, as you would see in the table of standard reduction potentials, is assumed to be taking place in dilute aqueous solution.

Actually, if it is in a standard state, the concentrations of the ions will be taken to be 1.0 molar, which is the standard concentration.

One thing that I regret about my lecture on Friday and about my lecture today is that I am not really talking too much about molecules and molecular shapes and what these things actually look like in solution. But normally, when you have metal or metalloid ions dissolved in aqueous solution, there is some number of water molecules that are interacting directly with the metal ions.

It is just not a so-called naked metal ion, but it is bonded to water molecules in solution.

And this is through the type of Lewis acid, Lewis base chemistry that we talked about earlier. There would really be some number of water molecules bonded here.

And we will look at so-called coordination complexes in quite a bit more detail in the upcoming section on chemical bonding, but this is how you will find it typically written in a book. And that is not representative of the structure in solution, which you do need to know in order to have a little bit of an understanding of the system.

And we are going to consider the possibility that indium may react with uranium to provide indium two plus.

We are going from trivalent to divalent indium.

And the source of that electron is the uranium three plus ion going to the uranium four plus ion.

There is a hypothetical reaction that we want to consider.

And we are going to need to be able to express that in terms of half-reactions.

And one of these half-reactions is simply indium two plus plus the electron. Sorry, indium three plus plus an electron going to indium two plus.

And, similarly, over here, we have uranium three plus.

I am writing both of these as reductions, as you will find them in the table. Four plus, plus an electron, going to uranium three plus.

Those are our two half-reactions.

Christine, can you zero in on them?

Yes, you are doing that already.

Thank you. -0.49 for indium.

And then, when we look at uranium, these are arranged alphabetically.

Here they are in alphabetical order.

In the tables they can be arranged by potential or they can be arranged alphabetically. Sometimes it is easier to find a potential by taking advantage of alphabetization.

And so, if we can focus in on that -- We focus in on that, and you will see that the 4+ going to the 3+ is -0.61.

And then you will remember that to find the standard cell potential, E zero of the cell is going to be equal to E zero of the cathode minus E zero of the anode.

And what we can see here is that this reaction is going to proceed spontaneously as written because in going from left to right, as written, uranium plus three is going to plus four. So, uranium is the reducing agent. And it is a stronger reducing agent than the other possible reducing agent, indium two plus, because it is more negative than the indium two plus. And how much more negative is it? It is more negative by +0.12 volts.

And we, therefore, because this cell potential is positive, we know that this reaction is spontaneous as written. And it is positive by 0.12 volts. That is a spontaneous reaction.

And now we have all the information that we would need in order to get the equilibrium constant for this reaction.

We know that, in terms of standard potential, it is 0.12. Let's see, here, if we can just calculate this.

All right. I am going to take this and zoom it a little bit.

We are going to put in Faraday's constant of 96,485.3, and also we are going to need the gas constant.

Everyone remember the value of the gas constant, 8.31447? And now, if we look over at our relationship between the equilibrium constant and the free energy over there. We took a free energy and we converted it into a standard cell potential.

Now we have it, so we want to solve for an exponential of nFE. n is one here because, in both cases, we have one electron being transferred in the half-reaction.

We have the exponential of F times 0.12.

And then, that is divided by RT.

And so we have R times 298.15 K.

And let me just make sure I get back over here and get another parenthesis in there and see what it is.

Our equilibrium constant, for that reaction, with a separation for the standard cell potential of only 0.12 volts, is about 106. The equilibrium constant says that the concentration of these ions multiplied together divided by the concentration of these ions multiplied together is based on the information contained in the half-cell potentials. So, that was pretty cool.

And we will now go ahead and talk about another relationship that we can get.

Over there, I was able to give you that relationship between the equilibrium constant and standard cell potential by remembering something from chemical equilibrium.

And now, we are going to do that again.

And we are going to remember that delta G for a reaction is equal to delta G nought plus RT ln Q.

That is something that you should remember from your studies of chemical equilibrium.

And the neat thing now is we know we have another relationship for the free energy of a reaction that is related to electrical work. We got that up there.

Now we can go, minus nFE.

Notice that what we are going here is we are considering what happens when we perturb a system from equilibrium conditions.

And when might that happen? Well, I showed you how to set up a Galvanic cell last time, and I showed you how to calculate its standard cell potential.

You could measure the standard cell potential by using, externally, a volt meter. And, as long as you did not let the reaction proceed to any significant extent, then you would know the standard potential for that cell. And what we are going to do now is we are going to say, let's let the reaction proceed.

Let's let a battery become discharged, for example.

And, as the reaction is proceeding, we might want, for example, to be able to make a plot of the potential at any particular extent of a reaction.

And, in order to do that, we will develop this equation, here, that shows how the potential at any particular point along the reaction going to completion is related to the standard potential.

And all I have done now is substitute minus nFE and minus nFE zero in, respectively, for delta G and delta G zero for the reaction. And now I want to go through and divide by minus nF. And when I do that, I am going to get E is equal to E zero minus (RT over nF) ln Q.

And this equation is very central to electrochemistry. It is the Nernst equation.

And you will be able to use the Nernst equation to predict how systems will behave when they are perturbed from equilibrium.

And one example would be that of a battery discharge, like I was mentioning a moment ago.

And so, let's kind of pick some arbitrary material, out of which to make a battery.

And we will use the Nernst equation to get information about how it will discharge. And let's consider the following cell. It will be one in which the two half-reactions are as follows. Iron two plus plus two electrons going to Fe metal.

And the other material will be cadmium two plus plus two electrons going to cadmium metal.

Now we need the two standard reduction potentials for iron two plus, -- -- which is coordinated in aqueous solution to six water molecules in an octahedral array, but we will get to that later. And I can see the equation but not the value. And there it is at -0.44.

And now we need cadmium two plus going to cadmium, elemental form. And we see that it is up there at -0.40.

Both cadmium metal and iron metal are negative of the standard hydrogen electrode. They are both reducing systems, as it were. However, we see that iron is more negative. And, since iron is more negative, if we set the cell up, if we have a piece of cadmium on one side and a piece of iron on the other side in this cell, then this piece of iron metal is going to be providing the electrons in this system, when we go in the spontaneous direction. The electron flow in the external circuit will be from the iron metal electrode to the cadmium metal electrode. And things happen in solution, as we've discussed, but that makes iron the anode.

And for the reaction going that way, as we would have set it up, then we have a standard cell potential E zero of +0.04 volts.

And now, in order to apply the Nernst equation to answer a question about this battery -- and this battery is not a high-voltage battery, it is only 0.04 volts, not high-voltage at all, so you probably would not use it for a battery, unless you really only needed a small potential difference in the first place -- but, nonetheless, we want to know how we can use the Nernst equation.

We can say, what is E at 80% completion?

That is the type of question we can answer using the Nernst equation. What is the potential drop to from an initial positive 0.04 volts when the reaction is 80% complete? Under standard conditions, we have one molar solution on both sides of the ions.

So, in this solution, we would have 1.0 molar candium two plus, and over here, in this solution, we have 1.0 molar Fe two plus.

Because those are the standard conditions, as you will see written in the header to that long table in your appendix, because you have to define standard conditions in order to have a standard potential.

And the standard conditions are 1.0 molar of the ions, respectively, in solution.

At 80% completion, what will happen is we will have gone in terms of producing iron two ions in solution. We are producing them in solution as the electrons flow through the external circuit because the piece of iron metal is the anode.

And so, what we are interested in here is Q.

I am writing backwards. Pretty soon I will be writing straight down or sideways. In the reaction, as written in the forward direction, we are producing Fe two plus ions such that we can define our Q at this 80% completion value as 1.8 molar divided by 0.2 molar.

And that is equal to, of course, just nine. Q is equal to nine.

We have RT, that will be 298.15 Kelvin.

RF is our number of Coulombs per mole.

That is the Faraday constant. And, in this case, because in the half-reactions, you have two electrons rather than one being transferred, n is equal to two.

If you plug in now, you have E zero is 0.04 and you have RT over nF ln of 9, that will give you the potential at 80% completion, which is somewhere in between 0.04 and zero, as this battery is discharged.

If you want to model the way in which a battery is discharged, you can use the Nernst equation for that purpose.

But, there is another type of cell that is interesting, that you can also describe very well using the Nernst equation.

This will be what is called a concentration cell.

Concentration cells are pretty neat.

In a concentration cell you set up a potential difference with the same electrode materials on both sides, just different concentrations. If I were writing this in terms of the type of diagram I used last time, I could show you that we could connect two beakers with a salt bridge like that and we could have electrode materials here dipping into solution on both sides. And, in solution on one side, we are going to have Sn two plus, divalent tin ions, at a concentration of 0.01 molar. And, on the other side, we will have Sn two plus at a concentration of 0.10 molar. This one on the left is dilute by a factor of ten. That one is the more dilute one by a factor of ten. And we can ask what kind of a voltage is set up as a consequence of just simply having different concentrations of tin ions in the two beakers.

And we can ask in which direction the electrons would flow in a system like this. Well, in this reaction, the system wants to go from a state where tin two plus ions at 0.10 molar go to the beaker where we have Sn two plus ions at 0.01 molar.

We have a potential setup here that is similar to the way osmosis takes place. The ions want to move from a region of high concentration to a region of low concentration.

And the system would come to equilibrium at that time when the concentration is the same on both sides.

And then there would no longer be any potential.

The value of E nought for this cell is equal to zero, because we have the same half-reactions that would take place on both sides. So, E nought is equal to zero volts in the concentration cell. And which way do electrons go?

Well, here is how you can think of it.

The electrode material can be made out of tin on both sides.

And, since tin ions are going to appear in solution on the dilute side, they are going to jump into solution from the electrode itself. A tin atom that is a piece of the metal on the surface of the electrode will jump into solution, increasing the concentration of tin two plus on the dilute side. And, every time it does that, we get two electrons racing through the external circuit, going over here, where those two electrons can be used to reduce tin two ions in solution that become a new tin atom on the surface of the electrode on the right-hand side. That is physically what happens to equilibrate the concentration of tin ions on both sides as a function of time. And so, what we can find is that these two values of the concentrations go into determining our Q in the following way.

We have Q of 0.1. Because the tin ions are going from a place of high concentration to a place of low concentration, and electrons are traveling through the external circuit defining the cathode and the anode in the direction that I mentioned, the electrons are coming out over here. So, the dilute side is going to be your anode. And we have n equal to two, in this particular case, because it is a two electron process that converts tin two plus into metallic tin. You can take these numbers and plug them into the Nernst equation.

And where you have E nought is equal to zero, n is equal to two, T would be 298.15.

We know the Faraday constant and the gas constant.

We have Q is equal to 0.1, which is our concentration ratio between the two sides. And, when we solve that, we are going to find that some small voltage is produced initially at this set of concentrations.

I hope that in the last couple of lectures, today and last Friday, I have hammered home the relationship between electrochemistry and energy. And next time we will go forward in talking about molecular structure and see how that is going to play a role.

Free Downloads

Video

• iTunes U (MP4 - 109MB)
• Internet Archive (MP4 - 193MB)

Audio

• iTunes U (MP3 - 11MB)

Caption

• English-US (SRT)