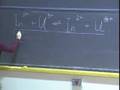Lecture 11: Why Wavefunctions are Important

Related Resources

Why Wavefunctions are Important? (PDF)

• Download English-US transcript (PDF)

This is the value of Psi, The following content is provided by MIT OpenCourseWare under a Creative Commons license.

Additional information about our license and MIT OpenCourseWare in general is available at ocw.mit.edu.

I just wanted to briefly remind you of some of the periodic trends that we talked about. As you go across the periodic table, both the electron affinity and the ionization energy increase. They increase because the nuclear charge increases. Remember, the potential energy of interaction is Z times e, where that is the nuclear charges, times e over 4 pi epsilon nought r.

Z increases as you go across the periodic table here.

As you go across, r is remaining the same because you are essentially still in the same shell.

And so what increases is that attractive interaction, meaning the electrons are more strongly bound, meaning ionization energy and electron affinity increases as you go across. And this also means, as you go across, r, the radius decreases.

The radius decreases again because Z increases.

The nucleus is pulling the electrons in closer.

Since they are all in the same shell, r is remaining the same.

And so, the overall effect is that the radius of the atoms decreases. As you go down the Periodic Table, the ionization energy and the electron affinity decrease.

They decrease because it is the r dependence, here, that takes over. Z is, of course, increasing, but not as fast as r.

As you go down the Periodic Table, you are going to shells that, on the average, are further out from the nucleus. And that dependence takes over, causing EA and IE to decrease. And then the radius, of course, increases, because, as you go down, you are putting the electrons into shells which are on the average farther away from the nucleus.

That is just a review of those trends.

Then, finally, I want to just define another term, and that is the electronegativity.

Sometimes we give that the symbol chi.

The electronegativity is an empirical quantity.

We are going to use Mulliken's definition for the electronegativity. There is a Pauling definition.

Mulliken is a little bit more straightforward.

And that electronegativity is defined as one-half times the quantity ionization energy plus the electron affinity.

The electronegativity is proportional to the average of the ionization energy and the electron affinity. The electronegativity is a measure of the tendency of an atom to accept or to donate an electron. If you look at the Periodic Table, here, you have atoms in the upper right-hand corner of This wave function is passing Here is the wave function. the Periodic Table. Well, they have high electronegativities. They are good electron acceptors. They have high electronegativities because they have high electron affinities.

Adding an electron to them means that there is a larger amount of energy release. The anion is much more stable than the neutral. And the electron affinity is minus that energy change, remember from last time.

These atoms here, with their high electron affinities, are good electron acceptors.

They are also good electron acceptors because their ionization energies are also high, which means you have to put in a lot of energy to pull an electron off.

They don't like to donate electrons, rather they are good electron acceptors. And then, the elements that are in the bottom left-hand corner of the Periodic Table have low electronegativities. They are good electron donors because their ionization energy is low in this part of the periodic table. You don't have to put in so much energy to pull an electron off.

They are also good electron donors because their electron affinity is low. You don't get as much energy back when you put an electron on them.

These are good electron donors. High chi, here.

These are good electron acceptors.

And one thing you already know probably is that some of the strongest ionic bonds are made between elements in these two corners of the periodic table. An ionic bond, as we are going to talk about, is one in which the electrons are not shared equally. And so these strong ionic bonds occur between elements with high electronegativity and low electronegativity. So that's that concept.

And then, finally, one other kind of odd and end here. That is this term isoelectronic. I have listed here a bunch of atoms and ions that are isoelectronic.

Isoelectronic means having the same electron structure.

All of these atoms and ions have the electron configuration 1s 2 2s 2 2p 6.

For example, this nitrogen, N minus 3, it has added three electrons to be nitrogen minus three. It has added three electrons to get this electron configuration, this rare gas configuration, this octet configuration which is a very stable configuration.

Aluminum has three electrons removed to obtain this particular electron configuration.

The common ions, ions that you see commonly in nature, are ions that, in fact, do have this octet configuration, this electron configuration of an inert gas. For example, you will often see compounds with nitrogen minus three.

You won't very often see a compound with nitrogen minus two or nitrogen minus one because those are not as stable as nitrogen minus three, given this rare gas or the octet configuration. All right.

That is just a little odd and end.

I just wanted to make sure that everybody was on the same level with the understanding of the word isoelectronic there.

Well, now what I thought I would do is talk a little bit about wave functions and the usefulness of wave functions.

This is going to be on the side boards here.

I wanted to just show you in kind of simple terms how a wave function actually determines the intensity of some transition.

Many of you have asked me about the intensities of transitions, and so I thought I would show you just a little bit about how these wave functions determine the intensities of transitions.

First of all, I have to explain this diagram to you. This is going to be a diagram for a hydrogen atom. That is what we are going to talk about here. What we are going to start with is an energy level diagram for the hydrogen atoms.

That is what this axis is. And so, I am plotting in that diagram, energy, going up.

And I plot the energy level for n equals 1.

I plot the energy level for n equals 2, n equals 3, all the way up to n equals 235, which is really very close to zero. That is part of what is on this plot right here, n equals 1, n equals 2, n equals 3. But then, what is also typically done on the same plot is that the potential energy of interaction is plotted as a function of r.

And so, on this axis here, kind of superimposed, is this distance r. And we plot often the potential energy of interaction. The potential energy of interaction kind of looks like that.

This potential energy of interaction is the Coulomb interaction, minus e squared 4 pi epsilon nought times r.

That is what that line is on this plot. Then what we do is we actually plot the form of the wave function, kind of on top of the energy levels. What we do is to say, for example, take the n equals 1 wave function, which starts at r equals 0 at some finite value and it is just an exponential decay.

And we plot it on this diagram, but we use the n equals 1 energy here as the value of Psi equals 0.

In other words, the n equals 1 wave function looks kind of like that. This level here is Psi equals whatever it is, at r equals 0, and there is just an exponential decay.

We plot the wave function on top of that energy level.

In other words, this is a complex diagram here.

You are going to see, if you take any course beyond this, this diagram a lot, with energy levels and wave functions plotted on top of them.

And then, the n equals 2 wave function is plotted on top of the n equals 2 energy level. Again, at r equals 0, it is some finite value and then it drops.

At some value of r, we have a node for n equals 2 here. The n equals 2 is the Psi equals 0. Right here, you have a radial node. Then it goes up and then it comes back. It goes down to a negative value and then comes back up. That is n equals 2.

And so forth and so on. n equals 3 looks like this.

It has two radial nodes. That is what that diagram is showing here. And then we get to n equals

Is this is a hydrogen atom and you have n equals 235, how many radial nodes do you have?

through this origin 234 times. That is the wave function.

And then it tails off. There is always an exponential dependence there. That is what that wave function looks like. Now, how do these relate to the intensity of some transition? Well, the intensity of a transition is related to the overlap between the wave function of the initial state and the wave function of the final state. What do I mean by overlap?

Well, by overlap, I mean you take the wave function, here, of the initial state, so I am going to pretend we have a hydrogen atom in the state, this is its wave function.

And that hydrogen atom is going to be relaxing to the n equals 1 state. What I am going to do, to get the overlap, is I'm going to take the product of the wave function of the initial state times that of the final state, and essentially I am going to integrate that resulting function.

I am going to multiply these two wave functions together, and I am going to integrate over all r the resulting function. That is what I mean by overlap.

But there is another term here. There is an r, too. That r is important.

It has to do with the transition moment dipole.

And we won't go into that, but it is there.

But it won't affect the argument I am going to make for you right now. We take the wave function of the initial state, multiply it by the final state times r, and then we integrate this whole thing from r equals 0 to infinity and then square it. That quantity is proportional to the intensity of some transition.

Let's do that. Here is Psi n equals 235, we are multiplying it by Psi of n equals 0 and actually multiplying it by r.

And what we are going to see, if we just look at this product here, if we just looked at Psi n equals 235 and Psi n equals 1, if we just looked at that product, we are going to multiply this times that.

In a graphical form, it is going to look like this.

It is going to go up, down, up, down, up, down. It is going to oscillate and then tail off in an exponential way because we are multiply this up, down, up, down, up down times this exponential decay. It is going to look something like that. But now, we are going to integrate this resulting curve. What you can see is that the area above this curve is equal to the area below this curve, approximately. And, when we integrate something, we are calculating the area underneath the curve.

These positive areas are going to cancel these negative areas.

The result is that this integral is going to be very small. And the result is that the intensity of that line is very low.

The intensities are proportional to this overlap, the overlap of the initial state wave function and the final state wave function. And you can see, here, graphically, how if you integrate that product in this case, the positive areas cancel the negative areas, and you don't have a very intense transition. However, suppose we look at the transition from n equals 3 to n equals 2.

Well, here is the n equals 3 wave function, here is the n equals 2 wave function.

And our intensity expression says that we have to multiply these two. Let's do that.

Let's multiply n equals 3 times n equals 2, here.

Well, the result, if you excuse my not so great drawing, is we start out with a very positive function here.

But then we have two negatives here, which make it a little bit less negative. But then, we have a positive, here, times a negative, and what that makes is a large area that is negative. And, if we go and integrate that, now we don't have the same cancellation of positive and negative areas. We integrate that, and that transition energy is large.

Or, that area is large, therefore the intensity of that transition is large. Bottom line, that is one of the elements that dictates the intensity of a transition. It is also one of the elements that dictates the intensity of your photoelectron spectra.

Somebody asked me about it the other day.

I had drawn lines in the photoelectronic spectra that were of the same intensity, 1s, 2s, 2p 6.

Somebody said, well, you have more electrons in the 2p state. Why don't you have a larger number of electrons coming off? The answer is, that is part of what goes into determining the intensity of the transition, but there is more to it.

It is not just the number of electrons.

Here is one of the elements that goes into determining the intensity of some transition. It is the wave functions and the overlap between the final and the initial state.

And then, I just wanted to also show you, here, for this atom in the n equals 235 state, I plotted just for fun, kind of schematically, what the radial probability distribution would look like. That is just r squared times the radial part squared. And, of course, since the wave function goes like this, oscillates, that is what the radial probability distribution is going to do. And you are going to see nodes here, 234 values of r, that is going to make the wave function be equal to zero. And then way out here, you are going to have a feature.

That last feature, here, is going to have the maximum probability, and that is your value of r that is most probable. It turns out for n equals that the most probable value of r is 43,800 angstroms.

That is about 4.38x10^-6 meters.

This is a really large hydrogen atom, n equals 235.

Do they exist? The answer is yes, they do exist. They exist, particularly in outer space, where there is lots of UV radiation to get these hydrogen atoms up into these very excited states.

And they exist in deep outer space, where the temperatures are pretty cold. And you need those cold temperatures because this hydrogen atom is not very stable in n equals 235. And, if you went and calculated here, I am going to draw a line, here.

This is going to be n equals 235, and this is the zero of energy. This energy difference here is about 4x10^-23 joules. Whereas, at room temperature, we will just talk about the thermal energy, thermal energy is about 4x10^-21 joules.

You can see that any little fluctuation at room temperature, since this is two orders of magnitude larger than what this bound by, any little fluctuation would kick this very weakly bound electron up and ionize it. And it would.

You really only see these in environments that are very cold, where you don't perturb what are called Rydberg atoms sometimes. I think in the laboratory the largest Rydberg atom that has been made is n equals 180 or n equals 200 or so. Anyway, that was really just for fun that I wanted to tell you about that.

Now, there is another little tidbit that I want to talk to you about that has to do with how knowing something about the energy levels in an atom leads to a nice practical device, like a helium neon laser. We have to take a look at the neon energy levels. And so we have another discharge lamp here, and we have some more of these glasses, here, so that you can resolve the neon lines here. The TAs will get them out.

Here is our neon discharge lamp.

You can resolve, here, the neon spectrum.

The spectrum that you should see should be what is shown on the side walls here. Let me turn off the lights so that you can see it a little bit better, hopefully.

You can see lots of lines in the case of neon because we have lots of different occupied states.

The glasses that I have actually are doing a phenomenal job in resolving those very closely spaced lines.

I must have a better quality glass today.

And, if you look at the side walls, you can see that I drew one of those lines. One of those emission lines is at 632 nanometers, which is the emission line of a helium neon laser. But it is really a neon transition that we will talk about in a moment.

I drew it as very thick on the board.

Because when I looked at the discharge lamp and drew that picture, my glasses did not resolve those lines so very well. And so that one looked really thick to me. At least my glasses, I can really see lots and lots of discrete lines.

But it is this transition, 632 nanometers, that is the output of the helium neon laser, which is the red laser that I use sometimes in the lecture, here, to point. It is the basis of the laser that is used in the grocery stores to scan the prices on your items. And it turns out that what is going on, here, is the following.

If you look on the side walls, we have neon in the ground state before we turn the discharge on.

And then, when we turn the discharge on, that pumps energy into the neon atoms such that one of those electrons, the 2p electron, gets promoted into the 5s state. And then, of course, that atom wants to relax. And so here it comes again.

That 5s state relaxes. That electron relaxes to the 3p state. And it is actually that transition that occurs at 632.8 nanometers, the basis of the helium neon laser. It is that transition, from the 5s to the 3p. It is not all the way down, but ultimately, of course, that state relaxes.

But what is going on in the helium neon laser?

Well, in the helium neon laser, we have a discharge ignited where we have a lot of neon atoms here in this excited state, with the one electron in the 5s state right as I show you. And that is emitting, a photon comes out. But what is happening here is that the photon that is emitted is able to, because of the construction of this laser, contact or to interact with another neon atom in this same excited state, that 2p 5 5s state. That photon interacts with this excited atom. When it interacts with that excited atom, what happens is that the photon stimulates that excited atom to actually emit a photon of the same energy. This photon stimulates this excited atom to release its energy right at that time.

The result is that you have two photons coming out.

They are going to come out in the same direction and they are going to be what is called coherent.

That is, their phases are going to match.

If you think now of the photon as a wave, they are going to be coherent. And the result is that you are going to have some radiation that is going to be twice as intense because they are coherent.

They are in phase. And then, what happens is that these two photons, they each then interact with another neon atom in this same excited state.

And each of those photons stimulates another atom to emit photons. And the result is now that you have four photons being emitted, the same frequency, same direction, and same phase.

And it is in this way that we amplify the light in any kind of laser. This is what is going on, this process of simulated emission.

Where you have a photon that now is exactly the frequency of the energy difference of the transition that you are going to make in this excited atom. This stimulates that atom to emit a photon. The two photons then come off coherently. And then, these two interact with two other atoms. Now you have four photons that are coming off. That is the process of amplification in any type of laser.

Of course, in order to make this work, you have to have a lot of these excited neon atoms around because you have to be able to have a photon interact with them before they just emit spontaneously. This is stimulated emission.

The other kind of emission that we were talking about is spontaneous emission. In other words, you have to have a high concentration of these excited neon atoms so that the photons that are originally emitted here, by just spontaneous emission, can interact with those excited state neon atoms and stimulate the emission and get this whole process rolling. In order to produce a whole lot of those excited neon atoms, what happens is we add in a little bit of helium. It turns out that in helium there are some excited states that are just, by accident, at the same energy as this excited state of neon. And the helium actually transfers its energy to the neon, into this state, and maintains, then, that very high population of neon atoms here in this excited state.

That is the function of the helium.

It is just the energy transfer from the helium excited state to the neon excited state. It keeps the population of the neon atoms really high. The helium, you don't see that emission. That is just a helper in this device. It is the neon transition that you are looking at here. That was just a short story about the usefulness of knowing about the energy levels in atoms and how ultimately you can make a practical device because you know something about the energy levels of your atoms.

Well, that is going to finish up, right now, our discussion of atoms. And now, it is time to move onto one of the very important parts of chemistry, and that is chemical bonds and the combination of atoms to form a chemical bond. That is what we are going to start talking about, now.

Today, what we are going to do is just talk about the fundamental interactions that are present in every chemical bond. Let's start with that.

Let me come over here while the lights are warming up so you can see that board. Suppose we have a hydrogen atom here, nucleus a, plus charge.

And it, of course, has electron a attached to it.

And way out here, we have nucleus b and electron b that is attached to it. And they are very far apart.

And so, in this case, where they are very far apart, the energy of interaction is just the energy of interaction between the electron and the nucleus, the electron-nuclear attraction. Here it is, the electron-nuclear attraction. However, as we bring these two hydrogen atoms together, at some point this electron that was only attracted to nucleus a is now begins to experience an attraction with nucleus b.

And this electron that was attracted only to nucleus b experiences an interaction whereby it is now attracted to nucleus a. And that kind of mutual attractive interaction then brings those two nuclei closer together. However, at the same time, when you bring those two nuclei closer together, you are bringing the electrons closer together.

And so there is an electron-electron repulsion that is present. In addition, as you bring these two nuclei together, what is happening here is you are having a nuclear-nuclear repulsion.

A chemical bond is really the sum of these three interactions and the interplay between these three interactions.

That is what we want to try to look at and try to understand.

How are we going to do that? Well, the first thing I am going to do is I am going to draw an energy of interaction as a function of the distance between the two hydrogen atoms.

I am going to take two hydrogen atoms and I am going to call the distance between them r. Now, I have changed my definition of r. r is the distance between the two nuclei. It is no longer the distance between the nucleus and the electron.

I have just changed my definition of r.

And I am going to plot the energy of interaction as a function of that distance between the two nuclei.

Here is my energy of interaction.

There is going to be a zero of energy, here.

I am going to plot this as a function of r, and the plot is going to look like this.

Way out here, where r is large, I have two separated hydrogen atoms.

The energy, here, is minus 2,624 kilojoules per mole. That is what this energy of interaction is, here.

Now, as I bring these two hydrogen atoms together, what happens is that this energy is going to decrease.

And it is going to keep decreasing until we get to some point. And then, as r gets even smaller, that energy of interaction is going to skyrocket and go to infinity. Starting about here somewhere, where the energy of interaction is less, is more negative than the separated hydrogen atoms. Well, what that means is that we are forming a chemical bond. The two hydrogen atoms are more stable then when they are separated.

The two hydrogen atoms are bound as soon as this energy of interaction gets more negative than the separated atom limit.

And it keeps getting more negative.

And, of course, the value of r at which that energy of interaction is a maximum negative number, well, that is the equilibrium bond length.

This is the most stable value of r at which the energy is the lowest. It is the most stable configuration. In the case of hydrogen, that value of r is 0.74 angstroms.

In this potential energy curve, as it is often called, everywhere where this energy of interaction is lower than the separated hydrogen atom limit, everywhere here, this is called the attractive region of the interaction potential. It is attractive because the hydrogen atoms bound are more stable than they are separated.

Or, the hydrogen atoms are bound.

They are more stable than the two hydrogen atoms separated.

We call this the attractive region of the potential energy curve. We also call this region, this attractive region, we call that the well.

And the well depth, here, from the bottom to the separated hydrogen atom limit, if you measure the energy from the bottom up, that energy is the bond association energy. We are going to call it delta E sub d, from the bottom here to the separated hydrogen atom limit. That is the bond energy.

432 kilojoules per mole is the energy that you have to put into the H two molecule to separate it.

You have to get it from the bottom of this well to the separated hydrogen atom limit here.

Now, you can also see, here, as you push those two hydrogen atoms even closer together than the equilibrium bond length, you can see that the energy is going back up.

And at some point, if you push the two hydrogen atoms close enough together such that the energy is equal to that of the separated hydrogen atom, it then becomes greater than that of the separated hydrogen atom.

From this value of r on, the hydrogen atoms are no longer bound because their energy is greater than the separated hydrogen atom limit. We call this part of the potential energy of interaction the repulsive part.

In other words, as you push the two hydrogen atoms closer together, they form a bond.

But if you push them too close, they are going to fly apart.

They are no longer bound. This is the general potential energy of interaction for every chemical bond.

Every single bond has this general shape.

That is important. But that shape is really a consequence of these three interactions that I talked about when we started this problem, here.

And so, what I want to try to do is now try to dissect that curve into the three components that give rise to that potential energy of interaction, that dependence as a function of r. I want to pull that apart.

This energy of interaction is the sum of the nuclear repulsion. Pushing the nuclei too close together, there is a repulsive interaction.

That is one of the interactions.

Plus, the electron-nuclear attraction is the attraction between the electron and the nucleus on which it came in.

And also between the electron and the other nucleus.

That is the electron-nuclear attraction.

Plus the electron-electron repulsive.

Well, when you bring two hydrogen atoms together those electrons are going to repel. That is the energy of interaction. It is the sum of those three fundamental interactions. But what I want to do is figure out an r dependence for each one of these interactions.

And the sum of that r dependence should give me a shape that looks like this. I want to see which interactions are important at what values of r.

Let me start. Let's start with the nuclear-nuclear repulsion here. If I wanted an r dependence for what that nuclear-nuclear repulsion looked like, what would that be?

Coulomb force. It is the repulsive Coulomb interaction. It is e squared over 4 pi epsilon nought r.

This is just two like charges that are repelling.

And so now let me draw that repulsive interaction as a function of r on an energy level diagram.

Here is my energy of interaction.

It is a function of r. There is going to be a zero here. And this repulsive interaction is going to be positive everywhere.

It is going to be infinite here and a one over r dependence coming down. This is the Coulomb interaction. This is the nuclear-nuclear repulsion. That is what it looks like as a function of r. That is one component.

Now, what about the other components here?

Well, it turns out I have no simple way of estimating what the r dependence is for the electron-nuclear attraction.

I have no simple way of estimating what the r dependence is for the electron-electron repulsion.

And I have no simple way of doing that for the sum of those two terms. Actually, the sum of these two terms, I am going to call the electron interactions.

Each one of these terms involves the electrons.

The is the electron-electron repulsion, electron-nuclear attraction. This term does not have any electrons in it. I have no simple way of telling you or estimating what the r dependence is of the sum of these two terms. However, what I can do is figure out what the energy is for the sum of those two interactions at two extremes. I can tell you what the energy is at r equal infinity, and then I can tell you what it is at r equal zero. And, therefore, on this plot, I am going to come in with a value for r equal infinity and a value for r equal zero.

I am going to draw a straight line as an estimate for the r dependence. Then I am going to add them up and see if the result looks, in fact, like this energy of interaction that I drew for you. And so that is what I am going to have to do on Friday. I will see you on Wednesday, if not sooner.

Free Downloads

Video

• iTunes U (MP4 - 106MB)
• Internet Archive (MP4 - 188MB)

Audio

• iTunes U (MP3 - 11MB)

Caption

• English-US (SRT)