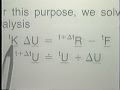Flash and JavaScript are required for this feature.
Download the video from iTunes U or the Internet Archive.
Topics: Beam, plate, and shell elements I
- Brief review of major formulation approaches
- The degeneration of a three-dimensional continuum to beam and shell behavior
- Basic kinematic and static assumptions used
- Formulation of isoparametric (degenerate) general shell elements of variable thickness for large displacements and rotations
- Geometry and displacement interpolations
- The nodal director vectors
- Use of five or six nodal point degrees of freedom, theoretical considerations and practical use
- The stress-strain law in shell analysis, transformations used at shell element integration points
- Shell transition elements, modeling of transition zones between solids and shells, shell intersections
Instructor: Klaus-Jürgen Bathe

Lecture 19: Beam, Plate, an...
Related Resources
Study Guide (PDF)
Readings
Section 6.5
Examples
Problems 6.20, 6.21
References
Bathe, K. J., and S. Bolourchi. “A Geometric and Material Nonlinear Plate and Shell Element.” Computers & Structures 11 (February 1980): 23-48.
Bathe, K. J., and S. Bolourchi. “Large Displacement Analysis of Three-Dimensional Beam Structures.” International Journal for Numerical Methods in Engineering 14 (1979): 961-986.
Bathe, K. J., E. Dvorkin, and L. W. Ho. “Our Discrete Kirchhoff and Isoparametric Shell Elements for Nonlinear Analysis: An Assessment.” Computers & Structures 16 (1983): 89-98.
Bathe, K. J., and L. W. Ho. “A Simple and Effective Element for Analysis of General Shell Structures.” Computers & Structures 13 (October-December 1981): 673-681.
Dvorkin, E., and K. J. Bathe. “A Continuum Mechanics-Based Four-Node Shell Element for General Nonlinear Analysis.” Engineering Computations 1 (1984): 77-88.
Bathe, K. J., and P. M. Wiener. “On Elastic-Plastic Analysis of I-Beams in Bending and Torsion.” Computers & Structures 17 (1983): 711-718.
Bathe, K. J., and E. Dvorkin. “A Four-Node Plate Bending Element Based on Mindlin/Reissner Plate Theory and a Mixed Interpolation.” International Journal for Numerical Methods in Engineering 21 (February 1985): 367-383.
Bathe, K. J., and E. Dvorkin. “A Formulation of General Shell Elements: The Use of Mixed Interpolation of Tensorial Components.” International Journal for Numerical Methods in Engineering 22 (March 1986): 687-722.
Lee, P.S., and K. J. Bathe. “Development of MITC Isotropic Triangular Shell Finite Elements.” Computers & Structures 82 (May 2004): 945-962.
Bathe, K. J., and P. S. Lee. “Measuring the Convergence Behavior of Shell Analysis Schemes.” Computers & Structures 89 (February 2011): 285-301.
The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high-quality educational resources for free. To make a donation or view additional materials from hundreds of MIT courses visit MIT OpenCourseWare at ocw.mit.edu.
PROFESSOR: Ladies and gentlemen, welcome to this lecture on nonlinear finite element analysis of solids and structures. In this lecture I'd like to discuss with you structural elements. Structural elements are, of course, employed to model beam, plate and shell structures and are most important elements. Because of their importance in engineering practice much research and development effort has been focused on the development of efficient structural elements. In this and the next lecture I'd like to discuss with you some modern effective elements.
We will first discuss shell elements and then beam elements and then we go back to use the shell elements, a concept that we discussed in some actual applications. When we do structural analysis we should keep one method in mind, namely that in a geometrically nonlinear analysis, a flat shell, referred to as a plate, goes very rapidly over into the behavior of a shell because of the curvature that develops as the plate deforms. Therefore, to analyze geometrically nonlinear plates we really are quite well off using general shell elements. And I'd like to now focus our attention on the development of general shell elements that we actually then employ to analyze plates as well as general shells.
There are various solution approaches that one can follow for the development of efficient elements. And one such approach is the use of general beam and shell theories. I'm thinking of beams as well as shells although I want to focus our attention on shells, really, in this first lecture. One starts with beam or shell theory as general as possible and develops the governing differential equations. From the governing differential equation one develops variational formulations and one discretizes those variation formulations using finite element interpolations.
This is the approach that is taken. The disadvantage of that approach is, in general, lack of generality of the approach. You're starting off with a particular shell theory, beam theory. You of course would like to have that shell theory as general as possible but you will find that really, the shell theory that you're starting of will mostly only be applicable to a certain class of shells. Therefore your finite elements that you're developing would also be only applicable to that same class of shells. And that means in engineering practice, in actual usage, the user has to be very familiar for which the particular element developed, as shown here.
I'll discuss now for what kinds of shells this particular shell element is really applicable. We would rather like to have shell elements that are applicable to any shell. Of course this is a very big aim, very difficult to achieve. But this is what we would like to have ideally in engineering practice. The other difficulty with this approach is that frequently a large number of nodal degrees of freedom have to be carried along in the development of the shell elements. And what I'm thinking of there is that you don't just have translations and rotations at the nodal points, which has engineering degrees of freedom that we would like to have and see in for the element, but you also have to have additional degrees of freedoms relating to the curvatures in the elements. And so on.
So this of course would mean, or does mean, difficult use of such elements and these reasons, these two reasons here have really driven the research and development efforts in different directions. Another approach is to use simple elements. Simple elements, but a large number of elements, then to model very complex beam and shell structures. As an example I'd like to just refer you to a 3-node triangle, a flat element in which the plate-bending behavior is modeled in a particular way and the plane stress behavior is modeled as a constant strain, constant stress element. These two are superimposed, these two behaviors are superimposed and you have a very simple shell element that in certain analyses can be quite effective.
Of course we have to recognize in this approach that the coupling between the membrane and bending action is only introduced at the element nodes. That is a major disadvantage. And that is the reason why you need so many elements to model a shell and that if we use a triangular 3-noded element with just a constant strain, constant stress element to model the membrane behavior, the membrane action, of course the membrane action is quite poorly approximated. And that is another reason why we need so many elements to model a complex shell behavior.
Here on this viewgraph I'm showing a picture of the element that I just referred to. Here you have a triangular element in the three dimensional space. Notice we introduce a local coordinate system, x bar 2, x bar 3, x bar 1. Local coordinate system, and in this local coordinate system we measure the displacements and rotations. And we superimpose for this element the bending behavior, the bending behavior corresponding to this degree of freedom, that degree of freedom and this degree of freedom at every node, of course.
We add, or superimpose onto this bending behavior the membrane behavior which corresponds to these two degrees of freedom. And we immediately notice that corresponding to this degree of freedom we don't have a real physical stiffness and we introduce a little artificial stiffness as shown down here. Now this artificial stiffness has to be selected and you want to select it such as to take out the singularity out of the system but yet make the stiffness not too big so as to destroy the behavior of the element. Because it's an artificial stiffness you really want to make it as small as possible just to take out the singularity out of this element when you apply this element in the modeling of general shell structures.
This artificial stiffness actually is quite bothersome in nonlinear analysis. It can provide problems and we really don't like it. But if we use this approach we have to introduce it and well, we have to, so to say, live with it, with the difficulties that we encounter. But the other approach that I want to discuss with you really quite extensively in these two lectures, namely using the isoparametric elements, having curved elements there as well, we don't introduce this artificial stiffness anymore because our experiences of introducing it in nonlinear analysis show us that there are many difficulties that come into the analysis procedure if you have this artificial stiffness. So we got rid of it. We don't need to use it any longer for the more modern elements that I will be talking about just now.
The approach for these modern elements is to use isoparametric interpolations and we talk then about the isoparametric (degenerate) beams and shell elements. "Degenerate" because we degenerate these elements, or we obtain these elements I should say, by degeneration from three dimensional behavior. We will talk much more about it just now. But in essence we are saying we take the 3-D continuum equations and we degenerate those equations to the particular shell behavior and beam behavior for beams that we would like to capture.
The resulting elements can be used to model quite general beam and shell structures. And that is, of course, a very large advantage in engineering practice if you can use the same elements to model a variety of structures. The basic approach of this isoparametric interpolation is to use the total and updated Lagrangian formulations that we developed earlier.
We talked in the earlier lectures quite extensively about the total updated Lagrangian formulation, the continuum mechanics equations, as well as the finite element discretization of the continuum mechanics equations. But we applied the final discretization only to 2-D and 3-D solid elements. Now we want to do the same for shell elements. We recall that in the T.L. formulation the governing equation is this one here, which is nothing else than the principal of virtual work operating on the second Piola-Kirchhoff stress and the variation on the Green-Lagrange strain. This integral has taken over the original volume of the structure, of the element, when we develop a finite element.
And this of course, the internal virtual work, and here we have the external virtual work. Notice the linearization of this left integral here resulted into these three integrals. We went through that linearization in quite some detail and we talked about the individual terms. I don't think it's now necessity to review that material anymore. Please refer to the earlier lectures. The same approach of course we used also for the U.L. formulation. Here is the general starting point, the principle of virtual work now, using second Piola-Kirchhoff stresses refer to the configuration at time t. Variations in the Green-Lagrange strains refer to the time configuration at time t.
This gives the internal virtual work corresponding to time t plus delta t, t plus delta t. And this is the external virtual work, same external virtual work of course that we are having in the total Lagrangian formulation. The linearization of the left hand side integral here results into these three integrals. Once again we talked about the linearization quiet extensively and if you refer to the earlier lectures surely you recognize individual terms that you're seeing here now.
We use these governing equations for the total Lagrangian and updated Lagrangian formulation to develop the general shell elements. And what we have to do now is to impose on these equations the basic assumptions of beam and shell action. And let us go now through these basic assumptions one by one carefully. The first assumption is that the material particles originally on a straight line normal to the mid-surface of the beam or the shell remain on that straight line throughout the response history. This is one most important assumption. You must have encountered this assumption or at least some form of it already earlier in your discussion of beam theories and possibly shell theories.
Let's look at this assumption more closely, so. For beams we would say plane sections initially normal to the mid-surface remain plane sections during the response history. This is basically saying the same thing what I just said earlier. And if you look at this closely you recognize that we do not say that the plane sections initially normal to the mid-surface remain plane sections during the response history and remain normal to the mid-surface. We don't say that. That's of course being said when you use the Euler-Bernoulli beam theory.
We don't say this, that the plane sections remain normal to the mid-surface throughout the response history. We don't say that and because we don't say that we in effect include in an approximate way shear deformations. In other words, we look here at the effect of transverse shear deformations is included, and hence the lines initially normal to the mid-surface do not remain normal to the mid-surface during the deformations. Let's look at what this means pictorially. Here we have a section of a beam at time 0 and we draw a line normal, that is, at 90 degrees to the mid-surface, shown as a dashed line. And we identify particles on that line. Here we have four such [? rad ?] material particles.
Now the beam will move, deform, go through large displacements, large rotations. But actually we assume small strains. And we see that these material particles which were originally up here are now down here. We identify that these material particles are still on a straight line. But this straight line is not anymore normal, that it is at 90 degrees to the mid-surface. And because it is not any more normal to the mid-surface we do include shear deformations approximately because we assume that the shear deformations are constant throughout the thickness of the beam.
This is a most important assumption. We're looking here what looks like a beam but actually, if you think of another dimension here, you can directly see that the same picture is also applicable to the motion of a shell. The second important assumption is that the stress in the direction normal to the beam or shell mid-surface is zero throughout the response history. In other words, there is no stress developed normal to the mid-surface. But notice that here is a stress along the material fiber that is initially normal to the mid-surface is considered.
Now this material fiber which is initially normal to the mid-surface will not remain normal to the mid-surface as I just said. And in the motion we will consider always this stress in the direction of that material fiber which was originally normal to the mid-surface. So after motion has taken place we are not really talking anymore exactly-- you want to look in great detail at what's happening-- we don't talk anymore exactly about the stress, that is normal to the current mid-surface. But we always talk about the stress in the direction of the fiber that was initially normal to the mid-surface. That's being said here.
And the third assumption, also most important assumption, is that the thickness of the beam or shell remains constant. Here then we clearly identify that we are using really a small-- we are assuming small strain conditions, but we allow for very large displacements and rotations. Well, with these three kinematic and static assumptions clearly identified we are now ready to actually develop the shell element interpolations. And let's go at that.
The first point is that we incorporate the geometric assumptions. Straight lines normal to the mid-surface remain straight, put here in quotes, that geometric assumption and the geometric assumption that the shell thickness remains constant throughout the whole motion. These were two assumptions that we just discussed. We incorporate that into our shell element formulation by using the appropriate geometric and displacement interpolations.
We incorporate the condition of zero stress normal to the mid-surface, I put it in quotes here, because remember, we are talking about the stress in the direction of the fiber that was originally normal to the mid-surface. We incorporate this condition by using the appropriate stress-strain law. Let's talk first about this assumption and then about this assumption, how we're using these to actually develop our shell elements.
To focus our attention I'd like to talk about a 9-node element. However. we will later on see that in practice actually we don't use the 9-node element very much. We actually recommend the use of a 16-node element and a 4-node element but this 9-node element in some analysis is also used. And it certainly is an element with which I can discuss with you, share with you all the experiences regarding the formulation of the elements because what we're talking about now really is applicable to any of the elements. In fact, we're talking about variable number nodes elements, where the number of nodes can be selected by the analyst and the geometric assumptions that we're now talking about are the same for any one of these elements.
How do we go about the formulation? Well, one important point is that we introduce at each node lying on the mid-surface, and here we see such 9-nodes, a director vector, a director vector t v n k, t referring already to the geometry at time t. Of course this director vector is actually input by the analyst for time 0 and then it evolves with the motion of the shell. Also we're introducing for the analysis, and that's being done automatically in the computer program, these two vectors here, t v 1 k and t v 2 k, which are normal to the director vector.
These vectors are calculated automatically in the computer program. We talk more about it a little later. Notice that the thickness here at this node is a k, and notice that v n k at node k-- k of course stands for that node-- acts into the direction off the thickness here. Notice that such [? triad ?] of vectors is of course being worked with at each of these nodes. And notice that the thickness at the nodes can change.
The element is defined as follows. As far as the analyst is concerned the initial nodal point coordinates of all the nodal points on the mid-surface must be input. Also the initial director vector must be input, here now you see the zero, and the thickness at every node must be input. Notice if these director vectors at all of the nodes are known, with the thicknesses at the nodes of course, then we can interpolate the thickness at any point of the mid-surface of the shell and we can interpolate the director vector corresponding to any point on the mid-surface.
Here such point on the mid-surface we get the thickness at that point, from the thicknesses that we have here, and from the director vectors. And of course we are also getting the director vector at this point from these director vectors. So the analyst must put in the nodal point coordinates of the mid-surface nodes and the direction cosines of these director vectors. Much of it of course can be generated in a practical analysis. We use an isoparametric coordinate system with coordinates r, s, and t.
The coordinates r and s correspond to a measure in the mid-surface. The coordinate t is measured in the direction of the director vectors. The geometry at time 0 is interpolated as shown here in this equation. 0 x i gives us the coordinates, three, i goes from one to three, of any material particle in the stationary coordinate frame. I should point out once more very strongly that we use a stationary Cartesian coordinate frame, x1, x2, x3, to describe the geometry of the element and to work with our element.
This coordinate frame, x1, x2, x3, is stationary. In that stationary coordinate frame of course we are measuring the coordinates of any material particle corresponding to time 0, corresponding to time t, et cetera. The same way as we discussed it in earlier lectures when we talked about the analysis of solids, 2-D and 3-D solids, and when we talked about the continuum mechanics equations. So here these coordinates of the material particles, as the material particles are moving through the stationary coordinate frame, are given by the right hand side. And what do we see here? k is 1 to n, n is the number of nodes for the element that I've shown you and would be nine. h k are the interpolation functions corresponding to the two-dimensional surface of the element.
In other words, these h k's are really the 2-D interpolation functions as we are used to see them for plane stress, plane strain, and axisymmetric analysis. Same interpolation functions. These are the nodal point coordinates at time 0. Here we have t, that is the third isoparametric coordinate. We talked about it just now. k, going from 1 to n again. a k are the thicknesses at the nodal points. h k here is exactly the same h k that you see here. And these are the direction cosines of the director vectors. Director vector n means director vector k, or normal. n really stands for normal, but it's really the director vector referring to the director vector k, of course, a node. 0 means time 0 and i means the components, the three components of the director vector. That's what we're looking at here.
Now if you leave this term out then you would have simply the interpolation of the mid-surface as for a membrane element, of course curved mid-surface. This term here is added in to take into account the effect of the shell thickness. Similarly at time t we have, applying the same interpolation t, x, i here now. Here we have t, x, i, k, same h k that we talked about earlier, same summing that we talked about just now. Here now t, v, n, i, k, the direction cosines, also director vectors. Director vector k at time t now.
Notice that all we have done in this term and in that term is to substitute for the 0 that we had here and that we had there, the t now. Of course this t means time t, this t here means coordinate t. That's why we put a circle around it and wrote it out there once more. This is the coordinate, the isoparametric coordinate t. r s coordinates go in here, t coordinate goes in there. What has happened here is that originally our director vector might look like shown in this picture here. The node coordinates are given here, 0 x i k, and in the time from time 0 to time t this director vector moves to look as shown now here. And of course the nodal point itself has moved as well.
So it's these quantities here, these [? rad ?] quantities that we're using here, which carries a curve. Well, to obtain the displacement of any material particle within the shell we proceed now exactly the same way as we have proceeded in the development of 3-D solid elements. We take the interpolation for the geometry at time t, subtract the interpolation for the geometry at time 0 and we get the displacements corresponding to time t. The result is this equation here. Here we have the displacements of any material particle in the shell. Here we have the nodal point displacements from time 0 to time t. Here we have the director vectors at time t, so to say, minus the director vectors at time 0. Really these are the direction cosines corresponding to the director vector at time t, minus the direction cosines of the director vector corresponding at time 0.
Of course this quantity here is obtained by this equation and that quantity here is simply obtained by subtracting the right hand sides corresponding to t x i and 0 x i the way you just have seen them on the previous viewgraphs. The incremental displacement from time t to time t plus delta t is similarly obtained from this relationship here. And the result is shown here where now we have here the increments in the nodal point displacements. And here we have the increments in the direction cosines of the director vectors from time t to time t plus delta t. The equation is given right there.
Well, with the equations that we have developed so far we are almost ready to establish the strain displacement matrices for the T.L. and U.L. formulations of the element. We have the coordinate interpolations for the material particles. We discussed those. And we have at the moment also the interpolation of the incremental displacements of the material particles in the shell element in terms of nodal point incremental displacements and the increments of the direction cosines of the director vectors at the nodal points.
What we, however, want is to have the incremental displacements in terms of the nodal point displacements and nodal point rotations. The nodal point rotations because the incremental nodal point displacements and nodal point rotations are the engineering type quantities that we can nicely deal with in a computer program when we analyze shell structures. So what we want is to express v n i k, the increments in the direction cosines of the director vectors, from time t to time t plus delta t in terms of the nodal point rotations. And that is achieved as follows. Here we have the stationary coordinate frame x1, x2, x3. e 1 is a vector into the x1 direction, e 2 the vector into the x2 direction, e 3 the vector into the x3 direction. Here we show v n k for nodal point k. In other words, a director vector, at time 0. This one is input by the analyst. These two are calculated in the program.
And of course there are such two for every nodal point k. For every nodal point k we also put in a director vector. Now the convention that is used, that can be used for the v 1 and v 2 calculations, that convention is given down here. Notice that if v n points into the e 3 direction then v 1 points into the 1 direction and v 2 points into the 2 direction. By that I mean into the e 1 and into the e 2 directions. Notice, this is a detail, that when v n points into the e 2 direction this formula breaks down and you need to use some other convention. But that is a detail. We don't really need to discuss that very much here now.
Anyways, let us say then at every nodal point k, v n has been input by the user, v 1, v 2, calculated by the computer program. We notice that these two are once again perpendicular to v n. Then we can directly say that the increment in the direction cosines of the vector, the director vector, is given via this relationship here. Now I've written this down already for time t. Of course it also holds for time 0, all you do is substitute for t, 0. It holds in fact for any time of the motion that we are considering. Let's see why this holds. Well, this picture here shows what's happening. Here we have v n, here we have v 2, here we have v 1. Notice alpha is the rotation about v 1, beta is the rotation about v 2.
Notice that with the rotation beta about v 2 here, we of course have an increment in this vector shown by this component because this here is now v n at time t plus delta t when alpha k is 0. When alpha k is 0. Now of course you would also have the alpha k component coming in and that means you have to add also this term. Notice that once you have obtained this vector you want to normalize its lengths again. But this picture here shows why this term is a correct term to use in this formula and you can extend this picture to also include this term. With this relationship we can substitute for v n and that's now done in this equation. We have substituted for v n and have now our increments in the displacements for the material particle within the shell in terms of nodal point incremental displacements and rotations about these v 1 and v 2 axes that we defined.
Well, having established this interpolation for the incremental displacements and, of course, the interpolations for the geometries of the element at time 0, at time t, we can directly establish the strain displacement matrices. And we will see we can then set up the k matrix, the f vector, the elements that go into the equilibrium equations the way that we discussed it in the earlier lectures. And from the solution of k u equals r or k delta u equals delta r in nonlinear analysis, we of course get our nodal point rotations, alpha k and beta k. And once we have calculated these nodal point rotations we obtain by this relationship here the v n at time t plus delta t.
In other words, what we're doing really here is we integrate over all of the angle, alpha k and beta k, to get a more accurate approximation for the nodal point vector, of the director vector, I should say, at time t plus delta t. Notice that if you do this integration in one step with the Euler forward method, you get back the equation that we had earlier on the viewgraph. And which I tried to explain or discuss with you using this picture that you saw.
And I mentioned also that after this integration of course we want to normalize the lengths of this vector to make it always a unit length vector. We recognize that with this approach we have only five degrees of freedom per node. Three translations in the Cartesian coordinate directions which are stationary, and two rotations refer to the local nodal point vectors v 1 and v 2 at time t. Now notice in geometric nonlinear analysis, of course, this vector and that vector, t v 1 and t v 2, change direction so our alpha k and beta k are rotations that are measured about changing directions. That is an important point to recognize.
Let's look at one pictorial representation of what's happening. Here we have node k. We have a smooth shell, say, that is discretized using four shell elements. I've taken one shell element away as shown here so that we can look into the shell. And at that node we have, as shown now, v 1 and v 2 at time t and the director vector corresponding to a time t. We measure at that time alpha k and beta k about v 1 and v 2. And we also measure the displacements of the node, u 1, u 2, u 3. So notice that this node moves as shown.
These are the three translational degrees of freedom and this director vector here moves to a new position and also changes direction. And that new director vector of course is given here in red. Notice that there is no physical stiffness corresponding to the rotation about the director vector. No physical stiffness. The five degrees of freedom that the element very naturally carries, u 1, u 2, u 3, alpha k, beta k. Alpha, beta at every node k.
If only shell elements connect to node k and the node k is not subjected to boundary-prescribed rotations then we only need to assign these five degrees of freedom to the node and only work with these five degrees of freedom at that node. However if we deal with a node to which also beam element is connected, which of course in general has three rotational degrees of freedom, or a node on which a boundary rotation other than alpha k or beta k is imposed then we transform the two nodal rotations, alpha k and beta k, to the three Cartesian axes. Because this way we can directly deal then with the connection here and the imposition of the boundary rotation.
We can do so directly using these three rotations now measured in the Cartesian axis directions. I mentioned already that the above interpolations for 0 x i, t x i and u i, in other words, for the original geometry, the current geometry, and the incremental displacements the way we have developed them, they can directly be used to obtain the strain displacement transformation matrices. And we really do so in the same way as for the 3-D solid elements which we discussed in an earlier lecture.
However, there's one method to recognize, and I briefly pointed it out also already in the earlier lecture, that using this expression here-- and I now must refer to the earlier material that we discussed-- using this expression to obtain the strain displacement matrix, we realize that we obtain the exact linear strain displacement matrix. However, using this expression here to develop the nonlinear strain displacement matrix, t 0 b n l, for the shell element only in approximation to the exact second-order strain displacement rotation expression is obtained because the internal element displacements depend nonlinearly on the nodal point rotations. I pointed that out earlier. Please refer back to that discussion to obtain a deeper understanding of what I mean here.
The important point, of course, is that we do obtain the exact linear strain displacement matrix, so at convergence in an iteration, k delta u equals delta r, when we have converged we actually have the exact solution to the model that we're using, of course. So this is important that we obtain the appropriate and exact t 0 b l matrix. The effect of what we are neglecting here was earlier mentioned and please refer back to that lecture.
We finally need to still impose the condition that the stress in the direction normal to the shell mid-surface is zero. Remember this was one further assumption that we discussed at the beginning of this lecture. We use a direction of the director vector as a normal direction. This means that at each Gauss integration point within the element, and which we want to evaluate the stress-strain law, we first of all set up a system of vectors, e bar r, e bar s, e t, that are mutually perpendicular. Now let's look here into the picture above and we see here at a particular Gauss point, schematically shown, the vector e r and e s which are vectors corresponding to the r and s axes.
e t is a vector corresponding to the direction of the director vector at that point. e t we accept as the normal direction, that's for the shell at that point, and we construct e bar s and e bar r to be vectors perpendicular to e t and to themselves. And that is achieved by this relationship here. Having now established e t, e bar r and e bar s, we use this stress-strain law. And by this I mean let's look first what's in these round brackets.
We use this stress-strain law corresponding to these directions. In other words, the directions e bar r, e bar s and e t where this is the normal direction, this corresponds to the normal direction e t. Notice by putting zeroes here we impose the fact that into the direction e t we have zero stress. Of course this matrix is symmetric. Notice we have k here which is a shear correction factor applied to the transfer shear stresses in the shell. New of course is Poisson's ratio and e is Young's modulus.
Now this is the material law corresponding to e t, e bar r, e bar s. And what we now have to do is transform this material law at every integration point to the global directions. Global directions because for the global x1, x2, x3 directions we have established the b, the strain displacement matrices. And that gives us this material, or c, shell. This q s h t, q s h is, I think, quite well known. Let me show you the form of it briefly.
It's a transformation matrix where we show some of the terms here, as you can see. And these terms, l 1, m 1, n 1, et cetera, are defined down here. And l 1, for example, is nothing else but the cosine of the angle between e 1 and e bar r. In other words, it's a transformation matrix that you are probably quite familiar with in linear analysis. It's the matrix that transforms the stress and strain components from one coordinate system to the other coordinate system. And of course the coordinate systems that we are transforming, that we're using here, are the bar, e bar, r, e bar s, e t coordinate system on the one side and e 1, e 2, e 3 on the other side.
Well, using this matrix we assure that the columns and rows 1 to 3 in c s h reflect that the stress normal to the shell mid-surface is zero. This holds true because, remember if we go back once more to the viewgraph, we have set this column and corresponding row to zero elements. And of course this means that the stress normal to the shell surface is zero. I should also briefly point out that we have a plane stress condition corresponding to the other direction of stresses, in other words, the e bar r and e bar s direction stresses. We have a plane stress condition as you can see here.
And of course this term would go with it as well. This term and these terms here reflect the plane stress situation in the plane of the shell, zero stress through the thickness. And all that we are transforming to the global system now here-- that fact, that physical fact-- of course must still be reflected in c s h. And that's what's being said here at that point. If you want to do plastic analysis, creep analysis, you proceed in the same way. But you calculate then once again the stress-strain metrics as in the analysis of 3-D solids. And having got that stress-strain matrix, six by six matrix, you impose the condition that the stress normal to the mid-surface is zero in much the same way as what we have done here for the elastic material condition.
Finally, regarding the kinematic descriptions that we talked about for the shell elements, it is interesting to note that also transition elements can be developed. These can be quite useful in practical analysis because they are elements with some mid-surface nodes that carry, in other words, associate director vectors and five degrees of freedom per node and some top and bottom surface nodes with three translational degrees of freedom per node. These elements would be used, for example, to model shell-to-solid transitions or to model shell intersections.
And here you see one such typical element just schematically shown. Here we have a mid-surface node, three translational degrees of freedom corresponding to the stationary coordinate frame, two rotational degrees of freedom the way we talked about it just now, mid-surface node here and top and bottom nodes here with three translational degrees of freedom for each of these nodes. Notice we can directly couple 3-D solids to this phase here and shell elements to this phase here.
We haven't shown mid-surface nodes here, but you would, say, have all the mid-surface nodes here and then surely shell element can directly be coupled into here in such situation as schematically shown right down here on this viewgraph where we have solid elements on this side and transition element right there and shell elements on that side. Because here you would continue with shell elements, you would continue with solid elements here. And once again three translational degrees of freedom for these top and bottom surface nodes and five degrees of freedom at shell mid-surface nodes as shown for that node right here. Notice we can also use these transition elements to model shell intersections very nicely as exemplified up here.
Well, this brings me to the end of what I wanted to discuss with you in this lecture. Of course what we have not done yet is to look at example solutions and what I'd like to do in the next lecture is first of all talk with you about beam elements, the isoparametric beam element, which is formulated much in the same way as the shell elements that we just discussed. And then I'd like to show you applications of the beam elements as well as the shell elements. So please, if you are interested in this subject matter, continue looking at the second tape, part two of this set of lectures. Thank you very much for your attention.