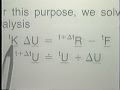Lecture 10: Solution of Nonlinear Static FE Equations I

Related Resources

Study Guide (PDF)

Readings

Sections 6.1, 8.4

Examples

Problems 6.1-6.4, 8.23, 8.24

References

Bathe, K. J., and A. P. Cimento. “Some Practical Procedures for the Solution of Nonlinear Finite Element Equations.” Computer Methods In Applied Mechanics and Engineering 22 (April 1980): 59-85.

• Download English-US transcript (PDF)

The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high-quality educational resources for free. To make a donation, or view additional materials from hundreds of MIT courses, visit MIT OpenCourseWare at ocw.mit.edu.

PROFESSOR: Ladies and gentlemen, welcome to this lecture on nonlinear finite element analysis of solids and structures.

In this lecture, I like to discuss with you solution methods that we use to solve the finite element equations in nonlinear static analysis.

In the previous lectures, we derived this set of equations, where tK is a tangent stiffness matrix. Delta Ui is a nodal point vector of incremental displacements corresponding to iteration i. t plus delta t R is the externally applied load vector corresponding to time t plus delta t. And t plus delta t F i minus 1 is equal to the nodal point force vector corresponding to the internal elements stresses at time t plus delta t, and at the end of iteration i minus 1.

The displacements are updated as shown here. Delta Ui, of course, is calculated from this set of equations. We add delta Ui to the previous displacements that corresponded to iteration t plus delta -- to time t plus delta t and iteration i minus 1. It's the end of iteration i minus 1. And this right-hand side gives us the new displacement vector corresponding to iteration i, end of iteration i.

Now this is one scheme that it's used to solve the finite element equations. We refer to this as the mortified Newton-Raphson method. However, there are other schemes as well. And schemes that are in certain problems much more effective. Since it is so important to use an effective method for the solution of the finite element equations because the costs can otherwise be very high, we should be familiar with those other techniques. And I'd like to share those now with you.

Therefore, we will look in this lecture at other techniques to solve the finite element equations. And we need, of course, to discuss convergence criteria. It's very important to use appropriate convergence criteria. Otherwise, you iterate too long and/or on the other side, you may actually stop iterating before you have achieved proper convergence.

So let me then go over to my view graphs and let us start the discussion here. The basic set of equations that we would like to solve are given here. Notice R is the vector of externally applied nodal point forces at time t plus delta t. And F is the vector of nodal point forces corresponding to the internal element stresses at time t plus delta t. Of course, this vector is unknown, and we want to iterate somehow to find it and make sure, of course, that at the end of that iteration, if we have the proper vector F, R is equal to F, or R minus F is equal to 0.

We assume that the loading is deformation-independent. If say, loading is deformation-dependent, we can also deal with that situation. But we will have to add additional terms to our iterative scheme. And I will get back to that a little later.

Notice that F in the total Lagrangian formulation the way we have discussed it earlier is evaluated by this product here integrated over the original volume for a single element and for the UL formulation, F is calculated as shown here. Here, of course, we integrate over the current volume, or the volume that we actually want to calculate. Notice in the iteration, of course, this volume here would be t plus delta t V i minus 1 as we will discuss just now. Because in the iteration, we always update this integral and that integral with the iteration counter that we are having on the right-hand side of the system of equations.

The methods that we use are based on the Newton-Raphson method, which is really used very abundantly to find roots of an equation.

A small historical note:

Newton gave a first version of the method in 1669. Raphson then generalized and simplified the method actually, in 1690.

Both mathematicians used the same concept. And both algorithms gave really, the same results. But it is very appropriate to refer to the methods that we're using as the Newton-Raphson method because Raphson really contributed quite a bit to that method.

So let us now consider a single Newton-Raphson iteration. The way you may have actually encountered it already earlier in your studies of solution methods for the roots of an algebraic equation. Basically, what you're doing is this. You're saying if you have xi minus 1, you calculate f at xi minus 1. You divide this value by the f prime at xi minus 1. And then this right-hand side gives you better value, a better approximation to the root of the equation.

Once you have xi, you repeat the process and you get xi plus 1. You keep on repeating the process until, basically f xi here is close to 0. Because then you have a root.

Well, if we use that Newton-Raphson formula, it is quite interesting to see how it has been derived. We can write for any point xi, a neighboring point xi minus 1, directly this equation here by a Taylor series expansion. And if we neglect the higher order terms, we get that f of xi is approximately equal to this relationship on the right-hand side.

Well, since f of xi is supposed to be 0, because we are looking for a 0 of the equation, we set it equal to 0. And here you see directly the formula that I showed you earlier. So this is a very quick derivation of the Newton-Raphson procedure.

Let us look at a mathematical example to see how the method works, and to get some insight into the technique. Let us choose a very simple example, not much to do with finite element analysis. Let us say that f of x equals sine x and that our starting value is equal to 2 for the iteration. You always have to choose, of course, a starting value for the iteration.

Then, in this column you see the values that are calculated in the successive iterations. And we also show here the error. It is interesting to observe that when you are close to the root, you have quadratic convergence. Meaning that the error here, epsilon becomes an error. Epsilon squared here. This is summarized on this view graph.

Mathematically, if we have that the error, Ei minus 1, is given by this equation here. Of course, there's an approximate sign here. Then the error in the next iteration will be of this order. So the convergence is really very rapid once we are close to the root.

Here we can see, however, that if we are not close to the root-- in other words, if we are too far from the root, and we pick a bad value, then we don't get to the desired root, which is pi. But we get a value that is far away from pi. It is also root, but certainly not the root that we are interested in.

So Newton-Raphson iteration is not always convergent directly, converging directly to the result that we would like to obtain. There has to be some care when we use that iterative scheme. And in fact, we have to be close enough just to basically say what has to happen. We have to be close enough to the root in order to have convergence to the root that we're looking for. And ultimately, if we do converge to that root, we will get quadratic convergence to the root. And that is, of course, very desirable. But the starting value is critical, as you can see here from this view graph.

Let us look pictorially at the solution process. Here we have our sine function. And we are looking for this root.

In iteration 1, we basically set up a tangent to that sine function at the starting value, x0. And we calculate x1 using this tangent as another estimate to the value that we're interested in.

Now in the iteration 2, we lay a tangent to the f function. Which, of course, is sine x, at the new value corresponding to x1. And with this tangent, we get to this value. And you can see already that we got closer to the desired value. We were this far away originally. Then that far away. And now we are only that far away. Notice our sine function has this value here. And certainly, it's not 0 yet. So we lay another tangent at that point. And that's being done on this view graph here.

Another tangent, and now we get much closer to the desired value. Right here, x3 is already quite close. But not close enough as shown by this value. It's not yet close enough to 0, this length here. And we lay another tangent to that point now. And that's shown on this view graph now. And we can see with the blue line being the tangent at this point, we get x4 very close to the 0 value that we are actually interested in. Certainly on this view graph, you can't see any difference anymore between x4 and the desired value. So this is basically the process that we are following through when we go from iteration 1 to iteration 2 to iteration 3 and to iteration 4.

Beautiful convergence in this particular example. And the reason being that x0 is close enough to the desired value, the desired root. Which, itself, of course, is close to x4. Four

Well, if however, we were to take a value that is not close enough and then we, as I showed earlier, we do not converge to the actual root. And this is shown here. For example, if we take a tangent at a point where f of prime is almost 0, then of course, this tangent throws us far away from this root. And we will converge to some other root. Of course, we don't want to use an exact 0 here because we have f of x divided by f prime of x. So with an exact 0, we could not [UNINTELLIGIBLE]. But a tangent that is close to 0, an f prime value that is close to 0, would throw us far away from the desired root. And that shows some of the difficulties using-- in fact, almost all iterative schemes that we may not get fast enough to our root. And in fact, we may never get to the root that we are looking for.

Well, let us then look at the Newton-Raphson iteration for multiple degrees of freedom. Here we have our R minus F that we want to be setting to 0. Or we want to rather, solve for the displacements t plus delta t U, which are the solution because this t plus delta t u displacements would give us this force vector. And this force vector equilibrates the R vector. Meaning f of U, this little f of U, is equal to 0. And that, of course, is what we want to achieve.

Notice that we have here, of course, now n degrees of freedom. Therefore, n equations to solve.

Previously, we only looked at one equation.

If we apply the same principle as before to this little f, namely we expand f as a Taylor series about t plus delta t U i minus 1, then we get this equation on the right-hand side. And of course, on the left-hand side, we have f of t plus delta t Ui. Notice they are higher terms, which we will neglect just as we have done earlier for the single equation. Because we are looking for Taylor series expansion about t plus delta t U i minus 1.

If we neglect this part here, we obtain directly this equation here. 0 on the left-hand side, because once again, we are looking for the displacements values for which f is 0. So therefore, we set this deliberately equal to 0. And on the right-hand side, we have f t plus delta t U i minus 1 plus partial f with respect to U times the delta U. This delta U is unknown, of course, that we want to calculate. And this delta U is nothing else then the difference between the U value in iteration i and the U value in iteration i minus 1.

Notice that this f is evaluated at t plus delta t U i minus 1.

Let us look now at this equation. And if we write it a little bit more out, we find that on the left-hand side, we have, of course, a vector of 0's. On the right-hand side, we have a vector of f i components, f1 to fn. All of which are evaluated at t plus delta t U i minus 1.

And then we have here a matrix, which is a square matrix in which the individual elements are partials of f i with respect to Uj. For example, f1, partial f1 with respect to U1 here. Partial fn with respect to U n here, et cetera.

This matrix here will give us a tangent stiffness matrix. Notice this matrix is multiplied by the vector of incremental nodal point displacements corresponding to iteration i.

If we remember that f, the little f, at t plus delta t U i minus 1 is equal to R minus 2 plus delta t F i minus 1. Capital F here, little f there, remember?

Then, the partial of little f with respect to U at t plus delta t U i minus 1 is given via this equation.

Now, please recognize that partial of R with respect to U is equal to 0 if the loads are deformation-independent. Of course, if the loads depend on the deformations, in other words, if the loads depend on the U displacements, then this would not be 0, and we would have to actually put a term in here, carry that term along in the solution of the nonlinear equations. But for the moment, we neglect this. We assume that the loads are deformation-independent. And then, this term is equal to 0.

This here is now giving us the tangent stiffness matrix. And it is written down here.

The tangent stiffness matrix is nothing else than the partials of capital F with respect to the U's, to the displacements.

The final result then is given on this view graph. We substitute all the information that I shared with you into the Taylor series expansion around t plus delta t U i minus 1. We get directly this equation here.

Notice tangent stiffness matrix corresponding to time t plus delta t and iteration i minus 1. Delta U i corresponding to iteration i we have to be very clear about this, that this is an increment in displacement from time t plus delta t iteration i minus 1 to iteration i.

And of course, the nodal point force vector. Externally applied nodal point forces go in here. And this is the nodal point force vector corresponding to the internal element stresses at time t plus delta t and at the end of iteration i minus 1. Evaluated differently in the total Lagrangian formulation from the way we're evaluating it in the updated Lagrangian formulation.

We talked about this vector abundantly in the previous lectures. We talked about this vector, of course, also in the previous lectures. We had in the previous lectures here at tK, a constant tangent stiffness matrix, which was set up at the beginning of this whole interactive process, and was never updated.

Well, here we now update that stiffness matrix. And I think if you look through the information that I just discussed with you, you recognize why we're updating it. We are doing so because we are always starting with the new Taylor series expansion about the point i minus 1. This set of equations if of course solved for delta Ui. We add delta Ui to what we had already in terms of displacements to get our new estimate for the nodal point displacements.

It is important to realize that the K matrix, which we are using in the solution process, is symmetric. Because first of all, we use symmetric stress and strain measures in our governing equation.

Remember that when we apply the principle of virtual work, we use Cauchy stresses and infinitesimally small virtual strains. Now notice that both of these tenses are symmetric tenses. Of course, these are the tenses we're using in the UL, in the updated Lagrangian formulation. In the total Lagrangian formulation, we use the second Piola-Kirchhoff stress in Green-Lagrange strain. Both of these measures are again, symmetric measures. Both tenses are symmetric tenses.

If we had introduced for a formulation non-symmetric tenses, for example a non-symmetric stress tenser, and of course, an energy conjugate non-symmetric strain tenser, we would have obtained a non-symmetric K matrix, which would be much more difficult to deal with. Much less cost effective in the solution process.

Also, please recognize that we interpolated the real displacements and the virtual displacements with exactly the same functions. Whereas this point here is a continuum mechanics point, this is really a finite element point.

If we had used different interpolation functions for the real displacements, then for the virtual displacements, or vice-versa, then we would have not necessarily obtained a symmetric K matrix. Of course, the most natural procedure is to use the same kind of interpolation functions for the virtual displacements as we used for the real displacements, and that's what we did.

Finally, we also assumed that the loading was deformation-independent.

If we have deformation-dependent loading, then if you go more back to the earlier view graph, then of course, this right-hand side vector R here would depend on the displacements. And there are basically two different approaches that one can take.

In the first approach, one simply updates this vector with the iteration, or with taking into account the current or last calculated volume and surface areas for the elements. So we would simply put here an i minus 1 up there.

The left-hand side matrix, we leave unchanged. And if that converges fast, certainly it's a very effective approach to use. We use that approach abundantly.

However, another approach is to actually take the differentiation of R with respect to the U's, the way we have been looking at it earlier on an earlier view graph, and then you get some components that you add to the K matrix. And that K matrix may then out to be non-symmetric.

However, if the loading is deformation-independent, then the differentiation of R with respect to the displacements U is equal to 0, and there's no component from that differentiation coming into the K matrix. And our K, of course, provided these are also satisfied, is symmetric.

The iterative scheme that we just discussed is referred to as the full Newton-Raphson method. Full because we are setting up a new K matrix at the beginning of each iteration.

The full Newton-Raphson method shows mathematically quadratic convergence the way we discussed it a bit earlier in the lecture. And that, of course, is always the case provided you are close enough to the root. This quadratic convergence only holds provided you are close enough to the root when you solve your equations.

In finite element analysis, it is also important to recognize that a number of requirements must be fulfilled. For example, in elasto-plastic analysis, the stresses and strains must be properly-- plastic strains must be properly updated. And similarly, the rotations in a shell analysis must be properly updated. So it is not necessarily the case that you automatically get quadratic convergence when you do finite element announces with a full Newton-Raphson method. It is very important to also, on the level of updating the stresses and the rotations, really do things properly in quotes in order to obtain the full quadratic convergence of the Newton-Raphson method.

We can depict the iteration process in two equivalent ways. The first way is shown here, the left. And it's really the way we've been discussing just now the solution of f equals R minus capital F. Where we want to solve for the root, the 0 of this equation.

Notice here we have in red the little f depicted. Notice that at this point here, we have t plus delta t capital F i minus 1. And t plus delta t R is this value.

Now, as we get closer to the root, which is of course, the point where the red curve crosses this U-axis, as we get closer to the root, this capital F will get closer and closer to the R. And that is, of course, when the little f is equal to 0. That's all we are showing here. Notice that we are setting up a slope f prime at the point corresponding to the i minus first iteration. And that slope brings us into this point, which will be the next point for-- or the next starting point for the next iteration. I should say, the point of starting with the next iteration.

Now, this is one way of looking at the iterative process. We can also look at it as shown here.

Notice we have here the R plotted now horizontally. The displacement vertically. Notice the R at a particular time t plus delta t is shown by this dashed line. And we really want to find this particular point here and the corresponding U displacement of course.

At this point, the little f is 0 and the corresponding U displacement is down here. Notice that at the iteration i minus 1, it's the end of iteration i minus 1, we have obtained this point here. The U displacement corresponding to that point is obtained by projecting down on the displacement axes. And this slope here, the blue line, gives us a tangent stiffness matrix slope.

These are two equivalent ways. This is here more like a force deflection curve, and we will use this representation now abundantly. But keep in mind, it's really the same thing if you look at it closely.

Well, modifications to the iterative scheme are the following. If we leave the stiffness matrix constant throughout a complete solution process-- in other words, tau is equal to 0 here. It's never updated. We talk about the initial stress method.

If tau is equal to t, where t, of course, corresponds to a particular solution step and meaning that the K matrix is constant, but it is updated as the beginning of a solution step. Then we talk about the modified Newton method. Modified Newton-Raphson method.

Or, we may also find it effective to update the K matrix only at particular solution steps, at certain times only.

We note that the initial stress method and the modified Newton methods are, of course, much less expensive than the full Newton method per iteration, however. We should add that many more iterations are necessary to achieve the same accuracy if we don't set up a new K matrix in every iteration. The initial stress method and modified Newton iteration technique do not exhibit quadratic convergence because to obtain quadratic convergence, you need to set up a new K matrix in each iteration. And of course, you have to be close enough to the root, to the solution that you're looking for.

Let us now look at a simple example. An example where we have just one degree of freedom. And where we deal with two load steps.

Here we show the force applied to the problem, or to the structure. In the first load step, we apply 1R. And then in the second load step, 2R.

Notice horizontally here, I'm plotting displacements. And the force displacement curve is shown by the red line.

Now, to obtain the solution for this displacement, U1, and that displacement U2, we, as we discussed, set up a K matrix, which corresponds to the slope, a slope on the red curve. And we iterate towards the sought solutions.

Here, we have the iterative process using the initial stress method. In other words, where tau is equal to 0 in our governing finite element equations.

This means that we are setting up a K matrix initially, and that K matrix is depicted here by the slope, the blue slope that you're seeing.

Now with this slope and this load applied, we get the displacement shown down here. Notice the left superscript means load step 1. The right superscript means solution after iteration 1. And this is the solution obtained from this triangle. Notice there's a blue line up there, going up there, and where that blue line crosses the dashed line, we pick up a vertical fine, black line. And that vertical black line cuts through the displacement axes at this particular value. So this is the solution of our first iteration.

Now, having calculated this displacement value, we go up vertically and get to the red line, the red curve. And that red curve corresponds, of course, to the internal forces. To the internal force I should say, corresponding to this displacement. There's a red dot right on that red curve. And at that red dot now, we've set up a K matrix again.

Now notice, in the initial stress method, we keep the K matrix constant. This means that the slope here of this blue line that goes through this red point is the same as the slope that we had earlier right here. With that slope and the out of balance load-- and let's look now very closely here-- that corresponds to the distance between this red point and that dashed line with this out of balance load and this blue slope, we get an increment in displacement shown right here. And that increment in displacement added to the previous displacement gives us this value down here. And in fact, this value is very close to the correct solution, the exact solution, which is the solution corresponding to the dashed vertical line here. Notice that the dashed vertical line is the exact solution to that dashed horizontal line. And our vertical black line, which we are calculating, is virtually on that dashed black line. So we can accept now, convergence.

Let's now go into the next load step. In the next load step, we want to, again, deal with a K matrix. And in the initial stress method, we use the same K matrix throughout the solution. Meaning that the slope now, which we are laying onto the red curve, that slope being this blue line, is the same slope that we used before in the first two iterations.

With this slope and the out of balance load corresponding to the distance between this horizontal line, the dashed horizontal line, and that dashed horizontal line because we conversed in the first load step. With that out of balance load, we get an incremental displacement shown from here to there. And that incremental displacement then, added to the previous displacement, gives us this value in displacement. Notice time t plus delta t or load step t plus delta t, which is here. Load step 2 and iteration 1, end of iteration 1. This is now our current displacement.

With this current displacement, once again, which comes from this triangle here, with this current displacement, we go vertically up and get to that red point, which lies on the force displacement curve-- internal force displacement curve more accurately. And now we have this red point, and we set up, or we use now, again, a K matrix. Of course, in the initial stress method we use the constant K matrix. So this slope is the same as that slope.

And now watch closely. From this triangle here, which corresponds to this out of balance load, which is the same as that out of balance load. Out of balance load obtained by putting here a horizontal line. Notice and the difference between the dashed line up there and the horizontal line given by my pointer is the out of balance load. Which of course, is the same as the distance between this red point and that dashed line. This out of balance load with this slope gives us another increment in displacement, which brings us to this value here.

We repeat that process and iteratively, we get closer and closer to the correct solution, the exact solution, which is the dashed vertical line here for the displacement. Because at that dashed vertical line, we are getting to that red curve.

Now, this is the initial stress method. And once again, the point here is that we kept the same K matrix throughout the solution process.

Surely, if you now were to look at this iterative scheme to obtain a faster solution, you would want to set up a new K matrix. In other words, once you have this displacement value calculated, you want to update the slope corresponding to the slope of the red curve. And if you do so-- in other words, you update this blue slope corresponding to the red dots that you have obtained in your iterative scheme. These red dots, of course, being different from what you're seeing here now. Then you would have the full Newton-Raphson method.

If you only update the K matrix or the blue tangent that we are seeing here whenever you have converged to an equilibrium point. Meaning when you have converged corresponding for the first load step in this particular case. If you only update the stiffness matrix once you have converged to this load-- for this load step, then you would have the modified Newton-Raphson method.

I think if you look at this picture with these possibilities, you will realize that surely, the full Newton-Raphson method with updating the slope after each iteration will converge fastest. And the modified Newton-Raphson method will converge a little slower than the full Newton-Raphson method, but still faster than the initial stress method.

Well, this then brings us to the end of the discussion of this example. I like to now introduce you to another scheme that can be very important when we solve nonlinear equations, finite element equations. And that scheme is the scheme of line searches.

The basic equations that we are looking at that we want to solve are once more depicted here. Tangent stiffness matrix, incremental displacement vector, externally applied loads, nodal point forces corresponding to the internal element stresses at time t plus delta t, and at the end of iteration i minus 1, beginning of iteration i, of course.

Notice I don't have an i on here, I just want to denote this for the moment as an incremental nodal point displacement vector, which carries, however, a bar.

Let us consider forming Fi using this equation where beta is an unknown.

We want to choose beta now judiciously. We want to choose beta such that, in some sense, R minus Fi is small. And we have to, of course, look at the mechanism that we use to make R minus F small in some sense.

Well, as a side note, we recognize that when this equation here is 0 for all possible U's, then clearly this must be 0.

In other words, if we were to say to ourselves, let's make this equation 0 for all possible U's. Then really, we would have solved this equal to 0. The reason, of course, for it is that we could choose here for U a vector, which carries 0's everywhere except a 1 in one location.

And if that is a particular row, then corresponding to that row, surely this vector here, this R minus F corresponding to that row must be equal to 0.

So if we were simply to use here the identity matrix, or if we were to construct the identity matrix by allowing n U's that are linearly independent, of course, because they all make up such vector but with a 1 in a different location. As a matter of fact, we want to use U1 with a 1 here, 0's everywhere. U2, 1 here, 0 here, everywhere else 0, and so on. To construct an identity matrix here. Then with that identity matrix, clearly R minus F would be 0 everywhere.

Of course, that is not a viable scheme really. But what we want to do is to choose a particular vector here so as to make R minus F still 0 in some sense. And the vector that is quite effectively chosen is the vector that we obtain from the solution of K delta U bar equals R minus F.

If we use that vector here, basically projecting the R, capital R, minus F onto that vector. And we look for this to be 0. Then we have so to say, searched in the direction of delta U bar and made delta U bar transposed times this vector here equal to 0.

How does this scheme work? Well, we add beta times delta U bar to the value that we had already from the previous iteration. And we search along beta such that this top here is much smaller than the bottom. In other words, STOL shall be a convergence tolerance.

Notice the way it works. We choose a value of beta. With beta known, we add this quantity to this one. We get a value here. We take this value, calculate Fi corresponding to that value, see whether the convergence tolerance is satisfied. If not, we have to choose a new beta. And like that, we choose new betas until we have satisfied this convergence tolerance. That's what we call line search. We are searching along the line given by delta U bar until this is satisfied.

It's a very important scheme, and this scheme can be combined with modified Newton iteration, with the initial stress method, and with full Newton iteration. And it adds a lot to the stability of the solution, of the overall solution or the nonlinear equations. We will find, or discuss applications just now. But at this point, we need to stop for a minute because we need to go onto a new tape.

Finally, I would like to discuss with you a method that we also find to be very effective in nonlinear finite element computations. Namely, the BFGS method. BFGS stands for Broyden-Fletcher-Goldfarb-Shanno. And in this method, we proceed as follows.

We calculate or define a delta i as shown here in this equation. And we define a gamma i as shown in this equation. We want to calculate the coefficient matrix such that this equation is here satisfied. In other words, given delta i and gamma i, we want to use the coefficient matrix that satisfies this equation. And that's basically what's being done in the BFGS scheme.

Pictorially then, we can show for a single degree of freedom system, say the F plotted along this axis. The U displacements plotted along this axis.

Notice here in green we show delta i. And we show here in green gamma i. And notice that the matrix that we want to use is indicated by this blue slope. Which is, in other words, given by delta i and gamma i.

Well, the BFGS method is an iterative algorithm, which produces successive approximations to efficient stiffness matrix. Actually, we actually work with the inverse of that stiffness matrix as I will elaborate upon just now. It's really a compromise between the full Newton iteration method and the modified Newton iteration method. It shows very excellent convergence characteristics in the solution of many types of problems. Let's look at the individual steps that we use when we apply the BFGS method.

We, first of all, calculate the direction of the displacement increment. Here we have delta U bar i is equal to K inverse, the inverse of the K matrix, corresponding to iteration i minus 1. And here we have the out of balance load vector.

Notice once again we do not calculate actually an inverse of a matrix. We calculate the LDL transpose factorization of a matrix, and then we, as I will just now show, update that inverse in the BFGS iteration by specific matrices of rank 2. We get to that just now.

Well, having calculated this delta U bar i, we use that delta U bar i in the line search to obtain a better displacement vector, a displacement vector corresponding to iteration i. A better value then just adding the delta U bar i to it by adjusting beta.

In other words, we choose beta in such way as to satisfy this equation here. This is, of course, the equation that we are now familiar with as being equation that shows that convergence has been reached in a line search.

Having now calculated the t plus delta t Ui and the corresponding t plus delta t Fi, we can calculate the delta i and gamma i. And therefore, apply the BFGS method. And that's now step three, calculation of the new secant matrix.

K inverse of iteration i is equal to Ai transposed k inverse of iteration i minus 1 times Ai. This A matrix is obtained as shown here. v wi transposed.

The vi and wi's are given as a function of the delta i, gamma i, and K i minus 1 value. You should look at the textbook to see the details of actually evaluating the vi and wi. But once you have vi, wi, you can calculate A. And clearly, by this equation then, you get a new stiffness matrix.

It is important to note that in this iterative scheme, only vector products are needed to obtain vi and wi.

And it's also then important to note that only vector products are used to calculate delta U bar i.

If this would not be the case, particularly here. Then of course, the iterative scheme would be very expensive.

Let me show you a bit of the details why we only need to use vector products to get the solution.

Here, we have one typical step of the iteration. Notice on the left-hand side, we have delta U bar i. The value of displacement increment that we want to calculate.

On the right-hand side, we have i plus wi minus 1 vi minus 1 transposed. In other words, the Ai minus 1 transposed. And we would have such matrices going on here until we are coming to the A1 transposed matrix.

Then we have the inverse of a stiffness matrix. Here, corresponding to time tau. And then we have the Ai matrices as shown here.

Now, notice that this total amount then is multiplied by the R minus F i minus 1, the out of balance load vector.

Let's now go through the computations that are required to get delta U bar i.

Here we have delta R. This delta R, the out of balance load vector, which I just call delta R, multiplies this matrix. But if you look at this multiplication, we find that this delta R times w i minus 1 transposed is simply a number. So it's one vector multiplication that gives us a number.

This number multiplied by v i minus 1 is just the multiplication of a number times a vector. It's very simple. And notice, of course, this delta R i minus 1 is also multiplying the identity matrix. So in this step here, we have really nothing else then a vector multiplication. The only vector multiplication that, in fact, is there, is this value, this vector here, times that vector there, transposed. That gives us a number. This number times a vector [UNINTELLIGIBLE] operation. And of course, this one here times the i matrix is just this vector by itself.

So in this step, what we obtain is simply another vector. We take this vector and repeat the process. And since the repetition is just what we discussed already, we find that we only need vector multiplications to roll up all of these multiplications up to here.

Then we have a vector multiplied by K inverse. Well, that involves only vector multiplications again, because we have already the LDL transposed factorization of tau k.

These vector multiplications result again, in a vector. And that vector multiplied by these matrices here in the same way as we have proceeded here, means again, only vector multiplications. So this very important step here only requires vector multiplications. And that makes this whole process really efficient.

In summary then, we have the following solution procedures that we feel are very effective. The mortified Newton-Raphson iteration with line searches.

Here we have the basic modified Newton iteration equation. And here we have the line search equation. We, of course, after each such solution, evaluate an efficient beta. A beta that makes U-- t plus delta U i a good vector when measured on the line search criteria the way I discussed it.

And these two equations then, summarize really the modified Newton iteration with the line search.

The BFGS method is another effective scheme. We use the BFGS method always with line searches.

And then, as a third option, the full Newton-Raphson iteration with or without line searches. The full Newton-Raphson iteration with line searches is, of course, most powerful. But it is also most expensive per iteration.

We should point out that these techniques that I discussed so far cannot be applied for post-buckling analysis. We will consider the solution of the response after buckling has been occurring, after the item load level has been reached in a forthcoming lecture.

The next view graphs summarize these schemes: the modified Newton-Raphson, the BFGS method, and the full Newton-Raphson method. And I'd like to just very quickly go through the whole solution process for each of these methods.

In the modified Newton iteration technique, we initialize our displacements corresponding to the beginning of the first iteration, the end of the 0 iteration as tU. And similarly, we initialize our force vector corresponding to the internal element stresses. We set i is equal to 1, the iteration counter equal to 1. We calculate a K matrix at the beginning of the load step, and we keep that K matrix constant.

We then go into this step here where we calculate the out of balance loads. Calculate a new displacement vector. And in this box here, we measure whether we have converged already. Of course, this convergence would only be measured after we have gone say, at least twice through the iteration process. Or rather, we have calculated this increment in displacement vector twice. Because at the beginning corresponding to i equal to 1, we have now this fairly large out of balance load. We have just incremented the load vector. Therefore, this right inside should be non-zero. And we would get an increment in displacements. And to measure how large that increment in displacement is, we really want to go through this whole cycle at least one more time.

We then, having calculated this incremental displacement vector with the bar on there, we perform a line search the way we discussed it to update our displacements corresponding to the iteration i. Of course, we only have come so far once through it, so i is equal to 1 still. And this gives us the accepted value of displacements corresponding to the first iteration.

We now increment our iteration counter, and go in to the second iteration.

Notice now in the second iteration, we have R minus t plus delta t F1 here. We calculate delta U bar 2. And now we would certainly measure convergence. And I will just now talk about how we measure convergence.

If we have not converged yet, we keep on cycling through here until we do actually get convergence.

The distinguishing feature of the modified Newton iteration is that we are having a constant K matrix. That we do not update the K matrix is this iterative loop here. It remains constant.

Remember in the initial stress technique, initial stress method, we would not even update the K matrix ever after the first time it has been calculated. But in the modified Newton iteration, we update it at the beginning of each load step.

In the BFGS method, we proceed as follows. We initial, again, our displacements and our nodal point force vector corresponding to the internal element stresses. We calculate tK. We calculate our incremental displacement vector with the bar on top. We measure convergence if i is greater or equal to. There's no point as I just mentioned, measuring convergence when you go first time through here. And we perform then the line search having calculated our actual incremental in nodal point displacement that we want to add to the previous nodal point displacements to get to this displacement vector. We, of course, also have this force vector.

We now can update our inverse matrix, our inverse secret matrix the way we discussed it. And we increment our counter. And we keep on cycling through here until we find in this box that we have converged.

In the full Newton iteration with line searches, we once again, initialize our displacement vector, our force vector, our iteration counter. We now calculate a new K matrix corresponding to the last conditions on displacements and internal forces, of course.

We enter here to calculate our incremental displacement vector with the K matrix that was just evaluated. And we measure convergence once again only when i is greater equal to. We perform a line search to determine beta in here. We therefore, update our displacement vector to the displacements that now correspond to the end of iteration i. We update our iteration counter. Or rather, increase our iteration counter. And we are calculating a new stiffness matrix corresponding to the last calculated displacement.

This is, of course, a distinguishing feature of the full Newton-Raphson method that we are calculating a new K matrix at the beginning of each iteration.

Well, these view graphs then, summarize the full process of iteration for the modified Newton, the BFGS, and the full Newton method. Notice that I have included the line search as the option.

If you don't have line searching, of course, it would simply mean that you set beta equal to 1, and skip that particular step of line searching. But in many cases, line searching is quite important. And certainly, can be necessary in some types of problems.

Let us now look at what happens in this box here. How do we measure convergence?

In each of these iterative schemes, we had such a box. And I like to look now more closely at how we measure convergence.

The measure of convergence should, of course, tell us, how well do we satisfy equilibrium? And there are basically three items that can be used. Namely energy, force, or moment, displacement, and rotation, of course, correspondingly as well. But these are the items that one can work with to measure convergence.

If you use an energy convergence criteria, and we are very fond of this one. You might want to use this equation here delta U bar i transposed times the out of balance load divided by delta U bar 1 transposed times t plus delta t R minus tF.

Now notice, this is the increment in nodal point forces, or the out of balance load, at the beginning of the load step. So this here is an energy corresponding to the beginning of the load step. And we are comparing here a similar quantity, but corresponding to the current load. Corresponding to the current iteration.

And if this quotient here is very small measured on that convergence tolerance, then we say we have converged. An important point is that in this convergence measure, we enter with displacements and with out of balance loads. Both enter in this convergence measure.

And please realize also that if the loads don't increase from time t to t plus delta t, meaning that this here is equal to 0-- 0 vector. Then, of course, we get 0 down here. And we could not apply this convergence criteria indirectly. Therefore, we would do is instead of 0 here, a reasonable small number in the computer program.

Also note that we apply this test here prior to line searching. In line searching, after line searching of course, this top part here is small. And we, therefore, do not want to apply this scheme here or this convergence measure after line searching. We should do it before line searching.

To measure convergence on forces, we can use this equation here. Notice here we have the out of balance loads. We take the Euclidean norm on the out of balance loads, and we compare that with RNORM, input by the user, by the analyst.

It is interesting, important to note that we introduce here only the components corresponding to the translational degrees of freedom. And here, of course, this RNORM is also a force corresponding, so to say, to a translational degree of freedom.

If we have also rotational degrees of freedom, then we would take instead of RNORM, RMNORM. And we would extract from these vectors, the components corresponding to the rotational degrees of freedom only. The point is that we want to have the same units up here as down here. Forces, forces, moments, moments. And we don't want to mix components from these quantities.

Of course, RMNORM and RNORM must be chosen by the analyst. The are input to the analysis as defined in the input to the computer program.

Typically, RTOL is 0.01. RNORM is simply the maximum of the NORM of the loads that are applied. Notice this Euclidean norm is evaluated as shown down here for a vector a. The symbolism, two bars each side with a 2 means nothing else then taking the squares of all the components of the vector, adding those squares up. And then, taking the square root out of that addition.

On displacements, we can also measure convergence. And here is the equation that can be used. The Euclidean norm on the incremental displacement vector. And that is compared with DNORM. Again, DNORM.

Notice that this here is again, input by the analyst to the computer program. It is part of the input that is provided for the analysis. And it's a reference displacement.

Notice then, of course, we should only include here the displacements, translational displacements in other words.

If we have also, rotational degrees of freedom. Then we would here include only the rotational degrees of freedom components and use here DMNORM. This way again, we compare one quantity with certain units with a quantity that has the same units. Once for translations and once for rotations.

And so when we have rotational degrees of freedom in the analysis, we this way make sure really, that the incremental displacements and incremental rotations are small at convergence. This then completes what I wanted to share with you in this lecture. Thank you very much for your attention.