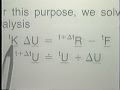Flash and JavaScript are required for this feature.
Download the video from iTunes U or the Internet Archive.
Topics: Demonstrative example solutions in static analysis
- Analysis of various problems to demonstrate, study, and evaluate solution methods in statics
- Example analysis: Snap-through of an arch
- Example analysis: Collapse analysis of an elastic-plastic cylinder
- Example analysis: Large displacement response of a shell
- Example analysis: Large displacements of a cantilever subjected to deformation-independent and deformation-dependent loading
- Example analysis: Large displacement response of a diamond-shaped frame
- Computer-plotted animation: Diamond-shaped frame
- Example analysis: Failure and repair of a beam/cable structure
Instructor: Klaus-Jürgen Bathe

Lecture 12: Demonstrative E...
NARRATOR: The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high quality educational resources for free. To make a donation, or view additional materials from hundreds of MIT courses, visit MIT OpenCourseWare at ocw.mit.edu.
PROFESSOR: Ladies and gentlemen, welcome to this lecture on nonlinear finite element analysis of solids and structures. In this lecture I'd like to discuss with you some example solutions. In the last lectures, we discussed quite a bit of theory related to finite element formulations and numerical algorithms, and I thought that you might like now to share with me some experiences regarding example solutions.
The examples that I'd like to discuss with you are first, the analysis of a truss arch, the snap-through analysis of a truss arch. Then the collapse analysis of an elasto-plastic cylinder. Then the large displacement solution of a spherical shell. Then we want to look at the analysis of a cantilever, the large displacement analysis of a cantilever when that structure is subjected to pressure loading. Once deformation independent pressure loading, and once deformation dependent loading. And then we would like to look at the analysis of a diamond-shaped frame. And finally, I'd like to discuss with you the failure and repair of a beam/cable structure.
So let me know walk over here to some view graphs which give us the information regarding all the analyses. The first example you're looking at is a simple truss structure which is shown here that is subjected to a load r here. Notice this is a two degree of freedom system only. Actually, if you use symmetry conditions you would have a one degree of freedom system. Notice the dimension l is equal to 10. k, the stiffness, ea over l, is given here.
You want to perform a post-buckling analysis of the structure using the automatic load step incrementation algorithm, and then perform a linearized buckling analysis. Notice that the two solution algorithms that we are using to perform these two analyses were discussed in the previous lecture. I assume in this lecture that you're quite familiar with what I have been discussing, particularly in the previous two lectures.
Let us start then with the post-buckling analysis. Analytical solution to this problem is given here, and actually, this solution is also given in the textbook. So please refer to the textbook for the derivation of this equation. The response can be plotted, and here you see is a plot of the load r as a function of the displacement data. Notice this, of course, is a critical point, a limit point. And the difficulty particularly is to march up here the solution algorithms, march across that limit point, and then down here, and further up here.
The automatic load step incrementation procedure that we discussed was employed with this starting displacement. One data is, of course, equal to 1u, and we set it equal to plus 0.1, and the solution obtained is given here. Notice this is a finite element solution, which of course is very close to the analytical solution.
The solution details for load step seven are given in this table here. Let's look at this table now a bit closer. At the beginning of that load step we have for the displacement, this value, and for the load, that value. As we iterate, i, of course, increases. We obtain this solution for the displacement, this solution here for the load, and these are here, the actual load applied, corresponding to t plus delta t lambda i, in other words. These are the incremental displacements, and these are the incremental load.
Now, as we discussed in the previous lecture, in the algorithm using the constant arc length, we see that the displacement here increases. The total displacement increases, of course. The total load here actually decreases. The incremental displacement for this step, as you can see, increases. The incremental load decreases. And that gives us, of course, this behavior that we talked about, namely that the displacement and load increments lie on this arc. That's why the constant arc length algorithm.
Pictorially, for this load step we can see the following. Notice here is our equilibrium configuration at which we are starting with iteration. Notice the final load increment that we want to obtain is given by lambda r. Notice the final displacement increment that we want to obtain is u. And we're iterating towards this u, and towards that lambda r, as shown further here.
In the first iteration we get lambda 1 of r, and lambda and u1. That gives us this point. In the second iteration we get that point. In this third iteration we get that point. And after the completion of the iteration, at convergence we end up on that point. Notice that if you take this point here and connect it with the iteration i point, you would get an arc around here. And that is, of course, a constant arc length algorithm. Also please, I should point out here that we have broken the scale as shown down here. So we are starting here already with 0.7 and here with 13.000.
The solution details for load step here, load step eight, are as follows. We used, for this particular load step, the increment of external work algorithm. The modified Newton iteration, as well. And these were the starting values now. And notice that we have immediate convergence. I pointed out in the previous lecture that for a single degree of freedom with the constant increment of external work algorithm, we will have convergence after the second iteration. In other words, the effective delta u2 is going to be 0. And that is shown right here in the table, and also in this picture here.
Notice here is load step seven. The equilibrium point at which we are starting off now, we want to of course walk along this red curve. Notice in the first iteration we come to this point c here. i is equal to 1. And then immediately we shoot down in the second iteration to the actual red curve. So we immediately converge, as pointed out in the earlier lecture, and on the earlier u graph. The u displacement is equal to u of 1 because delta u2 is equal to zero.
Let us now go and perform linearized buckling analysis for the same problem to estimate the collapse load for the truss arch. We talked about the algorithm that we're using for this linearized buckling analysis in the previous lecture. Here we have the actual load displacement curve. This is the collapse load that we would like to estimate in our linearized buckling analysis. Now, if we use delta t of r 1,000, our predictive collapse load is 25,600. Of course, our starting value, our t minus data tk is equal to 0k. I'm now referring, in other words, to the view graph that we saw in the earlier lecture, and the t minus delta t of k there is equal to 0k. The delta, the t of k is equal to data t of k now. And delta t of r corresponding to delta t of k is given right here.
Notice that this number is much larger than the number that we want to estimate. The reason being that the pre-buckling displacements are not small in this particular case. And I pointed out in the earlier lecture that that is really necessary, the necessary condition to obtain good results, acceptable results, in a linearized buckling analysis. It is not the case here, and that's why we are overestimating the buckling load, the collapse load, by quite a bit.
If we, however, increase our delta t value such delta t of r is 10,000, then you would see that our predictive collapse load is decreasing, and gets closer to the value that we want to obtain. As we increase our delta t of r value, and that means of course that we are getting closer and closer to the collapse load by this value here, we find that we are getting, in our prediction for the linearized buckling load, closer and closer to the value that we want to obtain. These values here, by the way, have been given to three digits. You notice that 15,000 certainly is very close to this value, but notice that the delta t of r value is very close to the buckling load itself, to the collapse load itself. This is something to keep in mind. The basic conclusion here is that the pre-bucking displacements should be small in the analysis in order to be able to obtain good results. By good I mean that the linearized buckling load will be close to the actual collapse load of the structure.
Let's look at an extension off this example. And that extension is given on this view graph. Here we have still our truss structure, but now we introduce here this spring. Let's called that spring k star. And this is the value that we give to that spring. If we trace out the load displacement response, that load displacement response is shown here. Load vertically. Displacement horizontally. And we notice that our stiffness matrix is always positive definite in all of this region.
So we don't really have a singular matrix, and we don't have what we might call a true collapse load. The structure is stable in some sense. Of course when we talk about a stable structure, we really have to also define what we mean by stability. In a practical analysis you might say, well, this displacement is just too much, and therefore I already consider this structure to be unstable at this particular location. You might want to say that, depending on your design criteria. However, one thing to keep in mind is that, in this particular example, we do not have a single stiffness matrix. The matrix stays positive all the way as we march up on that load displacement response.
Let's perform a linearized buckling analysis of this structure now. And when we take delta t of r equal to 10,000-- in other words, down here, our delta t of r-- we get tau r as a collapse load, 60,700. And if you take delta t of r 40,000, we get tau r 44,100. Notice that this is predicted by the computer program. However, we also know that there is no true collapse load in the sense of obtaining a single stiffness matrix. So, here we learn something more from this example. Namely that, in the linearized buckling analysis we may predict the collapse load, but there may not actually be a collapse load in the structure response corresponding to a single stiffness matrix. Whether you really want to accept this here as a collapse load depends on your design criteria.
Let's now look at another example, the second example. And in this example we want to consider the analysis of a cylinder that can undergo enough elasto-plastic conditions. The material data of the cylinder are given here. The geometric data of the cylinder are given here. Our goal is to determine the limit load of the cylinder.
The finite element method we're using here is shown on this view graph. Notice we have 8-node elements here. Four 8-node elements. And in fact, if we look closely at the response of the cylinder, we can identify that these middle nodes really are not necessary, because the response in the cylinder-- We assume the cylinder to be infinitely long. For that reason we have introduced plane strain conditions. The response of the cylinder is such that the same stress condition is obtained throughout the lengths of the cylinder. There is no variation in stresses along the length of the cylinder. And for that reason we could actually have analyzed the structure with 6-noded elements. In other words, we could have dispensed with these nodes here.
The internal pressure is shown here to which the cylinder is subjected. And once again we want to predict the ultimate load of this cylinder. Since the displacements are small, we use here an MNO formulation. In this load displacement, the response calculation, if we don't use the automatic load step incrementation- the one that we discussed in the previous lecture-- the analyst has to prescribe a load level, or a load curve, prior to the analysis.
And here we have chosen this load curve. Notice time is plotted along this axis. Pressure is plotted along this axis. And notice also that the elastic limit load is 7.42. Therefore this kink here is just above the elastic limit load. There's very little point in using a lot of steps here, because we know that an MNO formulation will reduce to a linear analysis until the heave point is reached. Or the elastic limit load is reached. So, we can go basically in one step right up to the elastic limit load, and then we take a series of steps to trace out the nonlinear response beyond the elastic limit load.
The purpose of the analysis was really to compare various solution algorithms-- the full Newton method with line searches, the full Newton method without line searches, the BFGS method, the modified Newton method with line searches, the modified Newton method without line searches, and the initial stress method. Now please recall that all of these techniques were discussed in the previous lecture, and I'd like to refer you back to that lecture to read up on this material if you're not very familiar with what I mean here.
The convergence criteria that we are using for the solution are given on this view graph. Notice here our ETOL, and here our RTOL. We saw these formulas in the previous lectures, and I don't want to go now through these formulas again. The only point that I should mention here is that this is a value you have to select. That is a value that you have to select. In the computer program that we are using, the ADINA program, of course, at default values, which are really working quite well over a large range of nonlinear problems, and those, of course, are used very frequently.
The RNORM here you have to select. And this is a reasonable number when you compare it with the total load applied to the cylinder. Notice that we're looking here at one radian of the cylinder. It's an axisymmetric analysis. When these procedures are used to calculate the force-deflection curve, we find that for p equal to 14, none of these procedures converges. The response is shown here that is calculated up to p equals 13.5. Of course, we have here drawn a smooth curve through the discrete solution points that have been obtained.
If we compare now the different solution techniques in terms of their cost effectiveness, we find that normalizing to the full Newton method solution time, we find that the full Newton method with line searches takes 1.2 times the time that is used in the full Newton method. The BFGS method has here 0.9. The modified Newton method with line searches 1.1. The modified Newton method 1.1. And the initial stress method 2.2. Showing that the BFGS is just a tiny bit more effective than the full Newton method, hardly worthwhile mentioning. But we also see that the initial stress method is twice as expensive as virtually all of the other methods. Once again please refer back to the previous lecture in which I have been discussing these various solution techniques.
If we use the automatic load step instrumentation we do not need to specify a load function anymore. We discussed that earlier. And the softening in the force-deflection curve is automatically taken into account. With this technique, these are the tolerances that we used. Default tolerances in ADINA here. And this is the same RNORM value that we used in the earlier analysis.
Now the displacement response is calculated as shown here. The p versus displacement curve follows this path. And notice that the computed limit load is really p equals 13.8. In the earlier analysis we could not go beyond 13.5. In other words, for a value of p equals 14 we did not reach convergence. We did not reach convergence because the limit load is 13.8. And this is the difficulty that I referred to at the start of last lecture.
You see, if you use the earlier solution algorithms, you have to very slowly this restarting, or a very judicious choice of a load function, get yourself closer and closer to the limit load. And that can be time consuming. That means it also consumes quite a bit of cost. Computer cost as well as cost of your time. And therefore, it is so much more convenient to use an automatic solution algorithm, that means you don't need to specify a load function, that's simply marches up here and gives you is the actual collapse load quite easily, as shown here. Notice an interesting point is that we actually march along this plateau when we use this automatic solution algorithm.
Let's look now at the next example. And this pertains to the solution of a spherical shell. Here we have a plan view of the shell. The edges are clamped. And here we have a side view of the shell. The shell is subjected to a concentrated load at its apex. And we will increase that load, as shown later on, to a very large value, so that this shell, schematically shown here once again, will undergo large displacements here. In fact, this point here will move, as my pointer shows here, all the way down to this level. Notice that this distance here-- and let me show it a little bit clearer here on the view graph-- is equal to .0859 inches. Here you see the other geometric data of the shell, and here you see the material data. We perform an axisymmetric analysis of this shell.
The finite element mesh is shown in this view graph. Here we have the original mesh subjected to the load. Notice that since we're looking at an axisymmetric analysis, and since we are using ADINA, we apply here a load of p, the total load divided by 2 pi, because we only look at one radian of the total structure. This 2 pi comes from the fact that we are only analyzing one radian of the structure. The deformed configuration for p equal 200 pounds is shown here in red.
Notice we undergo large displacements here, and that is also shown on the next view graph, which gives the force deflection curve obtained with this finite element mesh. And that force deflection curve is shown here. The linear analysis would predict this response. Of course, way off the actual response when the displacements become large. For this problem, the maximum load is 100 pounds, and we can apply that maximum load in one load step, or in a sequence of load steps.
If we apply the full load in 10 equal steps, we find that the full Newton method with line searchers works very nicely. The full Newton without line searches, in fact, is even more effective. Notice the BFGS method, the modified Newton method with line searches and without line searches. These three methods did not work. Of course, 10 steps to full load with these very large displacements means really using a very coarse load incrementation, or using, in other words, a very small number of load steps. These were 10 equal load steps, I should also say.
If we apply the full load in 50 equal steps, we find that the full Newton method with line searches is still most effective. And these four methods here converge. They are not quite as effective as the full Newton method, but the modified Newton method without line searches does not even converge. You would have to use many more steps to make the modified Newton method without line searches also converge. Here, the BFGS method compares quite favorably with these methods here. The convergence criteria employed for this problem are shown here. Notice ETOL is given here as 0.001 default in the ADINA program. We used a maximum number of iterations that we're permitted, which is very large. Very large in this particular case.
We, of course, may also perform the analysis using the automatic load stepping algorithm. Here we use as this tolerance ETOL, and RTOL this tolerance. Our norm is shown here. These are once again default tolerances in the ADINA program. The response that we calculate is shown on this view graph. Here, the applied load once again. Displacement at the apex. And this is the response calculated. Using as the initial displacement 0.001 inches. You get the solid curve. And using as initial displacement 0.01 inches, we get these points here. Notice, or recall please, that when we use the automatic load stepping algorithm, we start off that algorithm by specifying the displacement for the first load step at one node. And these are the values that I'm talking about here.
As a next example, I'd like to look with you at the analysis of the cantilever under pressure loading. Here we have the cantilever. This is the pressure loading applied. Notice it's quite a long cantilever, when measured on the gaps. Here are the material data. We analyze this problem using plane strain situation, and we want to perform the analysis for p equal to 1 megapascal. The interesting point here is to perform the analysis once with a deformation-independent loading, p the vertical and remaining vertical, throughout the whole analysis, and once with a deformation-dependent loading assumption, in which the pressure loading remains perpendicular to the mid-surface of the cantilever.
I think you can appreciate that if you have this situation, the deformations will be larger. Well, we performed both of these analyses, and once again the purpose here was really to contrast the assumption of deformation-independent loading with the assumption of deformation-dependent loading. The finite element model that we used consisted of 25 two-dimensional 8-node elements, one layer through the thickness, and they were evenly spaced. And here we list the solution details. We used the full Newton method without line searches. And the convergence tolerance is shown here. I should also add that we used 10 steps for the total load that we wanted to reach. 10 equal steps.
The force deflection curve is shown on this view graph. For small deflections, down here, there's basically no difference with respect to the assumption of deformation-dependent loading or deformation-independent loading. However, as the displacements become larger, the two curves part from each other and, as expected, the deformation-dependent loading gives larger displacements.
I should add here, if you look back at what we discussed in our earlier lectures, I should add that regarding the solution for the deformation-dependent loading case, we used a stiffness matrix that is symmetric. The same stiffness matrix, as a matter of fact, that we are usually using when we are analyzing deformation-independent loading. The deformation dependency of the loading was only taken into account by updating the right hand side load vector t plus delta t of r.
In our earlier discussions, we very largely assumed that t plus delta t of r is constant, and prescribed by the analyst. But I also pointed out in the earlier lectures that, if we have deformation-dependent loading, you would have a t plus delta t of r, superscript i minus one, where that i minus 1 then refers to the configuration corresponding to the i at the end of i minus first iteration. So, in this particular solution, when we dealt with the deformation-dependent loading, we kept this as the matrix difference [UNINTELLIGIBLE] on the left hand side, but we updated the load vector t plus delta t of r in the notation that we used in our earlier lectures for the configuration, and for the iteration, that we actually are dealing with.
And when we did so, we found that to obtain this total curve here, to obtain this total curve, we needed about 20% more solution time than for attaining this curve here. So, taking into account the deformation-dependency of the loading in this particular example just meant 20% more solution time with the computer program. Here on the next view graph now, we show pictorially how the cantilever has deformed. Here is the original mesh. And here is the deformed mesh when we use the deformation-independent loading assumption, and here is the deformed mesh when we use a deformation-dependent loading assumption. Notice, of course, that the deformations are larger when we have assumed that the loading is deformation dependent.
Let us now look at the next example. And in this example we consider a diamond-shaped frame. That frame is shown here. Notice we have a frictionless hinge up there and down here. We have a rigid weld here and over here. Notice that the frame is pushed down with a load p here, and is pushed up here. Of course, as deformations of the frame would be symmetric about this line here, notice that the beam cross section is one inch by one inch, and here are the material data for the beam. An elastic large displacement analysis is what we want to perform. We use twenty 3-node isobeam elements to model the complete frame. We will talk about the isoparametic, or isobeam elements later on in a later lecture.
Notice this is here 15 inches, and so is that. The deformations will be very large. In fact, this node here will go across all the way up to here, and that node we go across all the way down to here. The displacement of the top hinge of the frame is shown on this view graph. Notice here we are plotting the load p vertically up, and the displacement of the top hinge horizontally. Notice as the displacements are very large, you're going up to almost 25 inches here. Notice that for this solution, we used a load increment of 250 pounds. So we used 80 steps to come from zero to 20,000 pounds.
Notice this, of course, is a very large number of steps. You would have used another 80 steps here and so on. We wanted to use a small load incrementation because we wanted to obtain many solution points along this curve to be able to produce an animation of the frame response. And I'd like to now share with you this animation. We'd like to look at the animation. And I'd like to really look at the animation twice. First we will look at the animation of the frame response in very large deformations, very fast. And then we want to look at the same animation, but in a slower movement, so that I can also talk a little bit about it. Because the fast version is going so fast that I can't really say very much. So let's now look at this animation.
Here we see the frame is discretized by the isobeam elements. The two thick arrows show the load application. Here you see how the frame go through the last deformations. Let's now look at the same animation again with a somewhat longer time scale. We perform, of course, a static analysis. The time code above the picture of the frame gives the load step. You also see the load applied for each step. Here you see once again how the frame deforms when subjected to the loads. Certainly the frame undergoes very large displacements, and for the higher load levels the analysis represents only a numerical experiment. But surely an interesting one.
This completes our discussion of the frame analysis example, and I would like now to look with you at the last example in this lecture, namely the analysis of the failure and repair of a beam cable structure. For this analysis, we use one option in the ADINA program that is quite valuable, namely is the option of element birth and element death.
What this means is that we can assign certain elements that are born in the analysis as this step by step solution proceeds, and we can assign to certain element, so to say, their deaths. They are disappearing at a particular time. This kind of analysis option is very useful to simulate, for example, construction processes and repairs of structures. As well known, structures can, of course, collapse during the repair, or even during their construction sequence. And therefore it can be important to actually simulate this sequence of construction, or the repair of the office structure, also on the computer, to find out the particular construction sequence or repair of a structure that one wants to proceed with.
Here we have a simple cable beam structure. This is a cantilever beam subjected to gravity loading, and here the cable is hinged at this end of the beam and up there so as to support the beam. Notice the material data for the cable are given here, and there's no pretension in the cable. The beam itself has these material data. So we model the elasto-plastic response of the beam. Here is the mass density of to beam. The cross section is shown over here.
In this analysis, we simulate the failure and repair of the cable in the following way. In load step one, the beams sags under its weight, but is supported by the cable. From load step one to two the cable snaps. In other words, for example, if delta t is equal to 1. The time step delta t that we talked about in the earlier lectures is equal to 1, then at 1 this would be the load condition, and at time 1.5, the cable would snap, so that at time 2 at the end of the second load step, the cable is not anymore in the finite element system, and the beam now sags. It undergoes plastic flow at the built-in end.
Now, in the next steps, two to four, the new cable is installed and is tensioned until the tip of the beam returns to its original location, namely the location that it had taken at the end of load step one. This is quite easily simulated with this element birth and death option available in the computer program you're using. Notice one element dies, namely the cable element dies at time 1.5, say, and then at 2.5 the cable is again there, and at time 3 and at time 4 we see that the cable has been tensioned.
Here's the finite element model. We used two truss elements here to model the cable. And we used five 2-node Hermitian beam elements to model the beam. Notice for the beam element, we use five Newton-Cotes integration points in the r direction, three Newton-Cotes integration points in the s direction. In load step one, the active truss is number one. It's there. At the end of load step two, no truss element is there, because remember, between load step one and load step two, at time 1.5, if delta t is equal to 1, this one cable, this one truss element disappears. It dies, so to say. And then there is no more truss connecting this point to that point at the end of load step two. At time two.
Now, in the next load step a new truss element is born. Truss number two. It might be born, for example, at a specific time 2.5, if delta t is equal to 1. And now the truss is in position. It has been born. And we are tensioning it from load step three to load step four. In the solution we use the UL formulation for the truss elements and the beam elements. The convergence tolerances are listed here. Notice that because we have rotational degrees of freedom for the beam, we also use a tolerance RMNORM the way I describe it in the earlier lecture when we talked about convergence tolerances.
Let us now look at the solution algorithm performances. If we use a full Newton method with line searches all load steps are successfully calculated. The normalized solution time, say, is one. The full Newton method without line searches did not work. We could not use the full Newton method for this problem. The BFGS method in this particular case worked quite nicely, but it needed more time. Two and a half times the amount of time that the full Newton method required with line searches. Of course, the BFGS method always has line searches. And if you use the modified Newton method, with or without line searches, we did not converge in load step two. So, this shows that really the full Newton method with line searches is very powerful, and in this particular case it is even the cheapest. The BFGS method did also quite well, but is quite a bit more expensive.
The results in all of this analysis are listed in this table. Load step one, the displacement at the tip of the cantilever is shown here. The stress in the cable. And the moment at the built-in end. Load step two, this is the tip displacement. Please see the very large increment in the tip displacement, because the cable is gone. There is no more cable. And the moment at the built-in end has also increased a lot.
Now we have installed the repair cable, so to say, and in load step three we have reduced the tip displacement from 0.63 0.31 meters. The stress in the cable is given here. And the moment at the built-in end is given here. And in the final load step, we've tightened the cable enough to get back to the displacement that the cantilever had at its tip originally. Same numbers here. And the stress in the cable is given here. And the moment at the built-in end of the cantilever is given here.
The last view graph here shows the deformations of the structure pictorially. Here you see the deformations at load step one-- here the beam, here the cable. Notice that these displacements are magnified by a factor of 10. These are the deformations of the beam at the end of load step two. Notice there is no cable here, and also these deformations have not been magnified. Very large deformations. Load step three, at the end of load step three, we see the cable here, the new cable that has been installed. And we see also that the tip displacement of the cantilever has been reduced by tightening that new cable already up. Now, at the end of load step four, the displacement at the tip of the cantilever are the same displacement as we have measured at the end of load step one. Here again we have magnified the displacements by a factor of 10.
This then brings us to the end of this example. I wanted to show you this example really as a demonstrative example to indicate to you how this element birth and death option can be used quite effectively to simulate repairs of structures. In actual analysis you, of course, might want to use a finer finite element discretization and also a finer integration scheme to pick up the spread of plasticity more accurately. However, this example as a demonstrative example really shows to us how we can use this element birth and death option to simulate such processes as repairs of structures. And I think you can easily visualize how this element birth and death option can also be used to simulate construction sequences of structures.
This then brings me to the end of this lecture. Thank you very much for your attention.