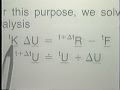Lecture 11: Solution of Nonlinear Static FE Equations II

Related Resources

Study Guide (PDF)

Readings

Sections 6.1, 6.8, 8.4

References

Bathe, K. J., and E. Dvorkin. “On the Automatic Solution of Nonlinear Finite Element Equations.” Computers & Structures 17 (1983): 871-879.

• Download English-US transcript (PDF)

The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high quality educational resources for free. To make a donation, or view additional materials from hundreds of MIT courses, visit MIT OpenCourseWare at ocw.mit.edu.

PROFESSOR: Ladies and gentlemen, welcome to this lecture on nonlinear finite element analysis of solids and structures. In this lecture, I would like to continue with our discussion of solution methods that we use to solve the finite element equations in nonlinear static analysis. We considered already in the previous lecture a number of solution techniques to solve this set of equations. t plus delta tr is equal to t plus delta tf, where t plus delta tr is the load vector of externally applied loads at time t plus delta t, and t plus tf is a nodal point force vector corresponding to the internal element stresses at time t plus delta t.

We talked about the full Newton-Raphson method, the modified Newton-Raphson method, the BFGS method, the initial stress method, and we discussed also convergence criteria. I've summarized here the equations corresponding to the modified Newton iteration. Now, a distinguishing feature of these solution techniques is that the analyst has to prescribe the externally applied load vector corresponding to all load steps.

This means schematically that if you have this kind of displacement load curve, or load displacement curve, shown here in red, the analyst has to prescribe prior to the analysis the load levels at which the response is sought. I've here indicated 1r as a load level corresponding to load step one, 2r as a load level corresponding to load step two, et cetera. Of course, the corresponding solutions that the analyst is looking for are the displacements.

Now, what might very well happen in practical analysis is that the analyst chooses certain load levels, and at the particular load level convergence difficulties are encountered. Too many iterations are required to converge, for example, in a reasonable cost. And typically, say, if this happens at this load step here, the analyst decides to restock. And this means that a solution corresponding to r4 here was not obtained.

I'm scratching that out. And the analyst restarts now with a smaller load step, namely indicated by these green lines here. The solution is obtained corresponding to that configuration, corresponding to that configuration, that configuration, which corresponds in this particular case now, to the level of r4, because we have three load steps to reach now r4. And say, at this point now, again, for example, we may encounter solution difficulties. The analyst is not able to obtain this solution here. Once again, the load step has to be smaller.

To continue the analysis, a restart is necessary at this particular configuration. And like this the analyst tries to get closer and closer to the collapse load. The conclusion is that we have difficulties in calculating the collapse loads when we use the techniques that I described in the last lecture. Of course, if you restart enough, if you use small enough to load steps, you will ultimately get very close to this collapse load, but this is tedious in a practical analysis, and we would like to have really an automatic scheme that directly can trace out the collapse load and you can also go into the post-collapse response, which is the response beyond this ultimate limit load here.

Well, I've prepared some view graphs to show you, discuss with you, a solution technique that actually can be employed to trace automatically load displacement response out, and go beyond the collapse load, as well. The idea is that we want to obtain more rapid convergence in each load step. We want to have the program automatically select load increments. And we want to also be able to solve for the post-buckling response. Now, this here means, of course, that a priori, prior to the analysis, you may not know, in fact you do not know, for which loads you will obtain the solution. We get the total load displacement response curve, but the discrete load levels at which the response was calculated is being decided by the program.

An effective solution would proceed as follows, schematically, of course. Here we have the load axis. Here we have the displacement axis. The solution scheme would start with large load increments in the region where the response is almost linear, then cut the load increments to a smaller size, and capture, of course, the ultimate limit load here, and then decrease the load, as shown here, to go into the post-buckling, post-collapse response. And the solution scheme, of course, could continue up this branch as well. And the solution scheme should automatically select the load step sizes, depending on the convergence that has been encountered in the previous load steps.

We compute now, t plus delta tr using this equation here. Notice that in this equation, t plus delta t lambda is an unknown scaler that is going to be determined by the program, and r is a vector that gives a particular load distribution. r is constant. It may contain the contributions of soft surface pressures, of concentrated loads, et cetera. The point is that r is constant and the program will automatically adjust lambda. Therefore, we assume in our collapse analysis that the loads are increasing and decreasing all in the same way as decided by one scale.

Of course, one could extend such an algorithm by introducing another vector, calling this r1, introducing a vector r2, with another scaler. And then have two scalers that have to be adjusted automatically by the program. And perhaps one can even think of three scalers, and so on, but then the algorithm would become quite complicated. So we look at a scheme that only has one scaler here, and one load vector that remains constant throughout the solution. As an example here, you see in blue the load intensity, t lambda r. Notice a concentrated load here, a pressure load here, and at the time t plus delta t we have the red intensity, t plus delta t lambda r, and of course this concentrated load has increased in the same way as the pressure has increased, as shown right here.

The basic approach of the solution scheme is shown on this view graph. Here we have the low displacement curve that we are looking for, shown in red again. Of course, loads plotted vertically, displacements plotted horizontally. Now, notice that if this is an equilibrium point, the red dot, and if you as the analyst were to chose an increment in load shown by this black line-- I'm putting my pointer now onto it-- then you can see that this black line defined by this load increment would mean that we have a large number of iterations necessary. If you need a large number of iterations, to converge to the new equilibrium configuration. In fact, you can see that this red curve is almost parallel to the black line, so we can anticipate large convergence difficulties trying to get to a solution with the load increment being equal from here to that black line.

The important feature of the algorithm that I want to present to you now, is that this load level is the first load level which we start in the iteration, but then the algorithm automatically cuts down this load level, as shown by this arc here, by the blue arc, until this equilibrium point is solved for. And this means that the convergence is much increased. In other words, the algorithm does not have great difficulties calculating this particular equilibrium point. And from here, of course, the same is repeated. And like this the algorithm goes along this red low-displacement curve, and traces this whole curve out.

Let us look a bit at the notation that I will be using, because it's important that we get familiar with it at this stage. Notice t lambda r, of course, is the load at time t. The corresponding displacement is tu. We used that notation earlier already. Notice that the increment in displacement from time t to time t plus delta t is u, shown here in green. Notice that the increment in the load from time t to time t plus delta t is, of course, given by the change in this load factor here. And that change in the load factor is lambda.

Now, this lambda value is also given in this equation here. It's buried in there. Notice this lambda of i here. We are writing it as a sum all of delta lambda k's We will solve for all these delta lambda k's And this lambda i, when i becomes very large, converges to the lambda that I have up here. Similarly, this ui which is written as the sum of the delta uk's this ui converges to the u that I'm showing here. So, u and lambda, shown in green here, are the exact values, the values that you want to converge to with lambda i and ui. Notice once again, delta lambda k, summing all these delta lambda k's up we get lambda i, and summing all the delta uk's up, we get ui. We should keep that in mind for the discussion that you want to go through just now.

The governing equations are now as follows. On the left hand side we have a tension stiffness matrix. In the modified Newton iteration we would have tau equal to t. Delta ui is our displacement increment vector. This is here, this scaler, t plus delta t lambda i, unknown. This one we know. And that one we want to calculate in the iteration i. In other words, this is an increment that is unknown at the beginning of the iteration. Here we have the nodal point force vector corresponding to the elements stresses at time t plus delta t, and at the end of iteration i minus 1.

Notice that this is a set of linear equations in the unknowns that are used. There are n such unknowns, and there's one more unknown here. So, we have n equations in n, plus 1 unknowns. We need, therefore, one more equation. And that equation is given by this constraint equation. The f here on delta lambda and delta u, some constraint equation here, gives us the additional equation that we need for the solution these n plus 1 coupled equations. The unknowns, of course, are these values here-- n plus 1 unknowns.

To solve these equilibrium equations, we can rewrite them as shown here. In other words, the equations on the finite element displacements can be split up, if you look at the previous view graph, directly into two sets of equations as shown here. The interesting point is that, this equation here does not involve a delta lambda. This equation here does not involve a delta lambda either. Now, having calculated from this equation this vector, and from that equation that vector, we can directly write delta u, as shown here, of course, now involving the delta lambda. And this is a form of equation for delta u that we will be using a little later.

And the first constraint equation I'd like to introduce you to, the one that I briefly mentioned earlier already, where we talked about an arc which is used to swing the load level around, so as to get to the low displacement curve very quickly, and that constraint equation is this spherical constant arc-length criterion, which is written here. Notice here lambda i, here ui. Of course both of these quantities create, in essence, beta factor and delta l squared.

Delta l is set at the beginning of the load step. Delta l, in other words, is constant throughout the load step. The value of delta l is chosen based on what has happened in the previous load steps. Having chosen delta l, you can calculate the right hand side, and on the left hand side, we have a constraint between the increment in lambda, and the increment in delta u. Remember, lambda I is the sum of all of the delta lambda k's and ui is the sum of all of the delta uk's I just showed that on the previous view graph. Therefore, if we substitute here, we get a constraint equation between the delta uk, and the delta lambda k. Well, here we have the definitions once more. Notice beta is a normalizing factor which is applied in order to make these terms here dimensionless.

The equation may be solved as follows. Using that lambda is equal to this equation here. ui is given as that. Of course, this here can be expanded using the information that we discussed earlier. And substituting for this value and that value into the constraint equation, we directly obtain a quadratic equation in delta lambda i Remember that these two vectors here are, of course, known. These two vectors are known, and that one is known also, because that was established in the previous iteration.

If we geometrically interpret this solution scheme, we find the following. Here we have our equilibrium point. Here is delta lambda, which is constant throughout the solution step. And let's assume the use of modified Newton-Raphson iteration. We start off with this tangent here at this solution point, the equilibrium point, and we iterate around this arc using the constant stiffness matrix at each of these points. In the first iteration, we get to this point. Second iteration, that point. Third iteration, that point.

And that signified also looking here to the displacements. Notice t plus delta t u1 is the displacement value calculated in the first iteration. This is the one calculated in the second iteration. That is the one calculated in the third iteration. We use a constant stiffness matrix here. Of course, we could also change the stiffness matrix, go in other words, to a stiffness matrix that has been updated in the iteration corresponding to the current stress and displacement conditions, and then convergence would be more rapid. But of course there would also be a higher cost involved, because whenever we calculate with a new stiffness matrix, and we triangularize that stiffness matrix, there's a considerable cost involved in doing so.

This is one scheme, and we find this scheme quite effective, except that when we want to calculate limit loads, we find that near the limit load the scheme can require quite a number of iterations. And so, we have been looking for other schemes that might do better in the range of the limit load. Well, here we have one other scheme, namely the "constant" increment of external work criterion. We have here quotes on the constant, because we are setting w on the right hand side in the first iteration, as shown here, and in the next iteration then, we have a zero here.

Notice w is a value that is calculated in each load step, and as soon as we find that the first scheme-- and obviously, constant arc lengths criterion scheme-- has difficulties converging, or marches too slow, then we switch to this "constant" increment of external work criterion, with a w from the previous step, the increment of external work from the previous step. We use that for the current step, and then this equation here gives us a constraint on delta lambda 1. Notice that this equation here means really that we are looking at is this area here, the shaded area, being w, and we want to have the delta lambda 1 in such a way that this shaded area w here is equal to what we have had as the increment of external work in the previous load step.

Well, this gives us delta lambda (1), and having obtained delta lambda (1), we can go into the next iterations, 2 to 3, and so on for i, and as I mentioned already earlier, we then have a zero on the right hand side. Otherwise the same left hand side. And this left hand side has now two solutions. This solution here is disregarded, because this solution would reverse the direction of the load, and we don't want to admit that. We want to basically have the load increase more and more until the total collapse of the structure is reached, and then of course it may decrease to go into the post-buckling response, but we don't want to have the load totally reversed, and so this is a solution that we now use for delta lambda (i).

Notice that for a single degree of freedom system, we would immediately find that delta u (2) must be zero. Why? Because we notice that the load vector is orthogonal to the displacement vector. Now, for a single degree of freedom system, of course, each of these are just numbers, and since the r is not zero, because that is of course a prescribed value prior to the analysis, this is not zero, delta u (2) must be zero. And that shows already the effectiveness, just show it a bit, of this algorithm.

All the algorithm altogether is now as follows. We specify r. In other words, the analyst has to specify the load distribution, concentrated loads, distributed loads, that shall be dealt with in this collapse analysis, and also the displacement at one degree of freedom corresponding to delta t lambda. This is done to just start the algorithm. Once the analyst has specified the displacement at one degree of freedom, the program can solve for delta tu-- in other words, all the other displacements-- and this delta tu corresponds to delta t lambda.

We feel that to start the algorithm it is easier for the analyst to prescribe the displacement at one node corresponding to delta t lambda-- Rather, to prescribe this displacement than to prescribe the first load level, because if you don't have much of an idea how the structure really behaves, it can be very difficult to give a load level that is reasonable, and is not too close to the ultimate limit load, or is already perhaps even beyond the ultimate limit load.

So we feel that this is a good way to proceed. For example, if you analyze the collapse of a shell, you may want to pick a node that you know will have non-zero displacement and assign at that node a displacement, say, one third of the thickness of the shell. That displacement then would give you delta t lambda, and surely would be less than the ultimate limit load of the shell.

This means, once you have solved for delta t lambda and delta tu, we can set delta l. The arc lengths for the next load steps. And now the program does everything automatically. It selects the increment in displacements and loads using this arc-lengths criterion that we just discussed. We use 1, which is the arc-lengths criterion, for the next load steps. We calculate w for each load step. When w does not change appreciably, or when there are difficulties with the arc-lengths criterion, with 1, in other words, then we switch to our constant increment and external work criterion. We call that the 2 criterion.

Once again, notice that delta l is calculated in each load step, and it is adjusted based on the number of iterations that we have been using in the previous load steps. In other words, if you go, say, up to load step three, and you have, say, obtained a solution up to load step three, the program has used a certain delta in load step three, and now the program looks at the number of iterations that were performed to get to the equilibrium position at the end of load steps three.

Based on these number of iterations, the program then cuts delta l down, or makes delta l larger, depending on whether the iterations were very many that you used, or were very few to get to the equilibrium configuration at load step three. So, the a program automatically adjusts delta l. Also notice that the stiffness matrix is recalculated when convergence is slow. In fact, a full Newton-Raphson iteration is performed automatically, the program switched automatically from the modified Newton-Raphson iteration to the full Newton-Raphson iteration when it is deemed to be more effective.

This is the automatic load incrementation scheme that I wanted to discuss with you. And I'd now like to go over to one other topic, a very important topic as well in the analysis of the nonlinear response of structures, and this is the linearized buckling analysis. In the linearized buckling analysis, we want to predict a collapse load, the buckling load of the structure via this criterion here. The determinant we know at the collapse point of the stiffness matrix is zero. The matrix is, another words, singular. The criterion that we use here determined of k is equal to zero, of course, means once again the k matrix is singular.

And that means that we really have a solution to this set of equations that is nontrivial. The trivial solution, of course, would always be u star is equal to zero, but that is not a real solution that we're interested in. A solution, a nontrivial solution exists to this set of equations only in the case when tau k is singular. And, of course, that is the same as saying that the determined of k, tau k is equal to zero. If tau k is singular the structure is unstable, and the collapse load situation has been reached.

Let's look at what this means physically. If we have here a beam. If we look at a beam, pinned at this end, pinned at that end, subjected to a certain load, then if the load takes on a certain value, the smallest imbalance of the load, a very small load this way, would immediately result in very large displacements. That's what the buckling criterion tells us. In other words, at tau r, the buckling load, the structure is unstable to any smallest load imbalance. Of course, the material data for the structure are given. And in this particular case, we use the data of an elastic beam.

In the linearized buckling analysis we want to predict the load level, and the buckling load shape corresponding to the buckling situation, by linearizing about a particular configuration that is not necessarily very close to the buckling load level. In fact, we assume that tau k is given via this relationship here, and tau r is given via this relationship. Notice here t minus delta tk and tk are known values, known stiffness matrices, and similarly, this load vector, and that load vector, and that one, are known values. Lambda is a scaler.

So basically, what we are trying to do in the linearized buckling analysis is to linearize about the configuration, not necessarily very close to the collapse load configuration, and establish with this linearized relationship an equation from which we can calculate an increment in load that gives us an approximation to the actual collapse load.

Pictorially, we are doing this here. We have here the load displacement curve in red. We have at displacement t minus delta tu, this load level. At displacement tu we have that load level. And if you linearize about these configurations here, using the stiffness matrices corresponding to these two load levels, we can predict a collapse load, which because of this linearization is, of course, not exactly the collapse load, but we hope that we are close to that actual collapse load.

Pictorially here, we do the following. Notice here we have the k plotted and the lambda value plotted. Along this axis. At a particular value, lambda equal to 1, we would have this point. Now let's look first along this axis here. Here we have tk. Here we have t minus delta tk. Notice tk is smaller than t minus delta tk. We are looking here, of course, at a single degree of freedom case again. This means that the structure becomes softer, we are getting closer to the collapse load.

In our linearized buckling analysis we put really through this point and that point a straight line. That projects us to a point, lambda 1, at which tau k is equal to zero. Corresponding to what we're doing here with the stiffness matrix, we have here also picture for the loads. Notice t minus delta tr here, tr there, and a straight line through it brings us up to tau r. Tau r is the collapse load. Tau r is the collapse load, linearized collapse load, corresponding to the value that we have here obtained for lambda 1.

The problem of solving for lambda such that the determinant of tau k is zero is really nothing else than an eigenproblem. And the eigenproblem that we have to consider there is written down here. Notice phi is an eigenvector, lambda is the eigenvalue-- unknown at this point-- and here we have a difference in matrices that we know, and once again the eigenvector. Notice one interesting point. That to establish this difference in matrix, all you need to do in the computer program is to store the previous difference matrix, and subtract from the previous difference matrix corresponding to load step t minus delta t, the current difference matrix.

This is interesting to note that because we don't need to separate out element difference matrices. We don't need to talk about nonlinear strain stiffness matrices coming from the elements, and linear strain stiffness matrices coming from the elements. We talked about, of course, these particular element stiffness matrices in previous lectures. We don't separate any out here. In fact, what we're doing, we simply take all of the contributions from the elements into account here, and all of the contribution towards element into account here, of course corresponding to time t minus delta t here, and corresponding to time t here. This therefore, is a very simple operation in the computer program.

And having established this eigenvalue problem, we can schematically look at the eigenvalues that would become calculated. Here we have some positive eigenvalues indicated, and here we have some negative eigenvalues indicated. Notice that there's a possibility of negative eigenvalues as well.

A physical problem that shows how you can get a negative eigenvalue is shown in this view graph. Here you have a structure, a frame structure, so to say, that is subjected to a compressive load and a tensile load. Now, notice that this compressive load would of course initiate buckling here, and there would be a corresponding to a positive eigenvalue. However, this tensile load has to reverse its sign in order for this member to buckle, and that would correspond then to a negative eigenvalue.

Now when we try to solve eigenvalue problems that have negative and positive eigenvalues, there can be difficulties with the eigenvalue solution method that you're using. It is easier for a solution method to simply deal with eigenvalues that are only positive. And for that reason we are reformulating the basic eigenvalue equation into this form. Here you have now the eigenvalue problem simply rewritten, really, with gamma being the eigenvalue, and phi still being the eigenvector, gamma of course, being a function of lambda.

With this eigenvalue problem then, we have only positive eigenvalues on gamma, of course, and we are interested in finding the smallest gamma value. Because the smallest gamma value corresponds to the smallest lambda 1 positive value. And of course, sometimes you also want to calculate gamma 2 corresponding to the second smallest positive lambda value, and so on. The negative lambda values lie over here.

The value of the linearized buckling analysis can be summarized as follows. The buckling analysis is not very expensive. It gives insight into possible modes of failure. For applicability, however, the pre-buckling displacements should be small. And very important it is that the buckling analysis yields modes, buckling mode shapes, that can be very effectively used to impose imperfections onto a structure and to study the sensitivity of the structure to imperfections.

Many structures are very sensitive, particularly shell structures, are very sensitive to initial imperfections in the geometry, and this linearized buckling analysis gives us the mechanisms and means to calculate mode shapes that we can impose onto the perfect structure as a geometric imperfection, onto the geometry of the perfect structure, to study then the behavior of the structure subject to these imperfections.

But it is very important that the procedure be only employed with great care, because the results can be quite misleading. The buckling loads that you might calculate in the linearized buckling analysis, these buckling loads may be way higher than the actual buckling loads that you should be using in your design. And we will actually show some examples in the next lecture pertaining to this particular problem here.

And one should always keep in mind that the procedure really predicts only physically realistic buckling loads when we have structures that behave close to the Euler column type. In other words, that buckle with very small initial displacements, or pre-buckling displacements, I should say.

Let's look at an example. Here we have the example of an arch subjected to uniform pressure. The geometric data of the arch are given here. The material data are given as well. Notice it's an elastic arch. And it's an arch with cross section b and h here, being both equal to 1. We also want to consider only the two-dimensional motion of the arch. In other words, two-dimensional action. We do not allow out-of-plane bucking for this arch.

Now the finite element model that we select for the arch is a model of 10 2-node isoparametric beam elements. We will talk about these isoparametric beam elements-- we call them also isobeam elements-- in a later lecture. And for the two-dimensional motion of the arch, we model the complete arch. The purpose of the analysis is to determine the collapse mechanism, the collapse load level of the structure. And not only this particular part, but we also want to calculate the post-collapse response of the structure.

Let us now go through the solution that was performed for this arch. As a first step we calculated the linearized buckling loads and corresponding mode shapes. And we calculated two. Interesting to note that the first mode corresponds to this pressure, and it's an anti-symmetric mode. The second buckling mode shape looks like this. It's a symmetric buckling mode shape. Notice that, in other words, the anti-symmetric buckling mode corresponds to a lower load than the symmetry buckling mode shape.

Having performed the linearized buckling analysis, we next use our automatic load stepping algorithm to calculate the displacement response of the arch as the load increases. Here on this view graph, we have plotted the pressure vertically up here, and the displacement of the center of the arch horizontally. Notice this black curve here shows a computed response using about 60 steps in the analysis. Notice it is a collapse load, of course, here, and this is a post-collapse response.

It's interesting to note that the collapse load predicted using the buckling analysis and linearized buckling analysis given by this blue line lies below this actual ultimate load predicted for using the automatic load stepping algorithm. And we have to ask ourselves why is that the case? Well, the computed response of the the perfect symmetry arch does not allow the anti-symmetric displacements to take place, and it is the anti-symmetric displacements that, of course, initialize, so to say, anti-symmetric buckling response.

We have computed the response of a perfect symmetric arch that is subjected to a perfectly symmetric load, and this does not allow the anti-symmetric buckling mode of the arch to come into effect. However, a real structure will contain imperfections, and hence it will go into the anti-symmetric behavior, and the actual collapse load will be below the one that we have predicted in our first analysis using the automatic load stepping algorithm, and the results of which I've just shown you.

Therefore, to really obtain a realistic collapse load, we have to now impose onto the perfect symmetry arch a geometric imperfection which allows the anti-symmetric behavior to take place. And we do so by adding to the geometry of the arch to the nodal point coordinates of the arch a multiple of the anti-symmetric mode shape. This collapse mode is scaled so that the magnitude of imperfection is less than 100.

This resulting imperfect arch is, of course, no longer symmetric, and we now solve for the response of that arch using our automatic load stepping algorithm again. This is the response that you'll see. Pressure and displacement of the arch. Notice this is well below the linearized buckling analysis solution, the blue solution, that I showed you on the earlier response graph. And this is here a much more realistic estimate for the collapse load of the arch. This is the realistic estimate that you would be using, for example, in the design of the actual structure.

It's also interesting to look at the deflective shape of the structure, and here we have the deflective shape of the perfect arch, of being symmetric at this displacement value. And here we have a deflective shape of the imperfect arch at this particular displacement value. Of course, this one is not a totally symmetric deflective shape.

Well, we have discussed now quite a number of solution schemes that we use to solve the finite element equations in static non-linear analysis. We have looked in the previous lecture at some schemes-- the full Newton-Raphson method, the modified Newton-Raphson method, the BFGS method, the initial stress method-- in which we have to prescribe the load levels. For each load step we have to prescribe the load level prior to the analysis, by the input of the computer program, and in this lecture I have shared with you some experiences regarding an automatic load stepping scheme regarding linearized buckling analysis. What we have not done yet, really, in my opinion is to look at enough examples, and that's what I would like to do in the next lecture. Thank you very much for your attention.

Free Downloads

Video

• iTunes U (MP4 - 98MB)
• Internet Archive (MP4 - 98MB)

Caption

• English-US (SRT)