D4M Session 6 Demo

• Download English-US transcript (PDF)

The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high quality educational resources for free. To make a donation or to view additional materials from hundreds of MIT courses, visit MIT OpenCourseWare at ocw.mit.edu.

PROFESSOR: All right, so we're back. We're going to do the examples we just described in the previous notes. And again, once again, these are in the-- if you have your d4m directory here, they're in Examples, Applications, BioBlast. This shows you the two programs we're going to run. We just have two examples.

And then we're going to be comparing two pieces of actual data. So if you look at this, this shows you what that data looks like. So sequence ID, and then very long sequences here. It'd be sure nice if they were all the same length, but they certainly are not the same time. They vary dramatically here you can see. Look at that guy. What's he doing? Super long.

So this is a reference bacteria dataset. This is known data. And this is a sequence here of some data taken from somebody's palm. This is open source data, so this is just an example of that.

And so you can imagine one would want to do a comparison of the data, of what the DNA sequences of bacteria on the person's hand are with some reference dataset. So obviously, we're not going to be using a dataset. This is a very small dataset here. We wouldn't expect to have any matches here and we're not going to have any, but this just shows you how that works.

So let me go over here, and so the first one here was this BB1. All right, so what we've done is we set our word size. We're going to use 10 base pairs, so that's where we're basically dealing with 10-mers. And wrote a little program here that what it does is given a CSV file, FASTA file, and a word size, it then creates the associative array as we described. So basically each sequence will be a row. So we'll get into that.

And likewise, each 10-mer will then be a column. And so we do this for the two datasets. Here is our matrix multiply, so A1 times A2 transpose gives us A1, A2. And here's is our pedigreed matrix multiply, the CatKeyMul A1, A2 transpose, and gives us A1, A2 key.

And so we can now look at that. So A1 has 198-- that's the bacteria-- 198 sequences with 8,001 unique 10-mers. A2 had 1,000 sequences with 2,365 unique 10-mers. And then when you matrix multiply them, you see that 85 of the 195 in the reference had a match with 415 of the 999 in the sample. So we're losing about half in each case because the associative rate does not store empty values. There's going to be no key which is a completely empty row or a completely column.

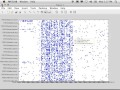
So we can now look at that data. So if we look at Figure 1 here. So this is A1, so this shows you-- again, here, why don't we zoom in? So that gives you better sense of the structure. You can actually click on that. So here's a 10-mer that appears in an awful lot of things. So basically this 10-mer appears in an awful lot of things. And these are examples of a row corresponding to a particular sequence ID.

So that's A1. That's the reference. A2, the sample, pretty much the same type of thing. Although a little bit different structure-- more these dense things, maybe. Why don't we zoom in on one of these blobs here? See those type of blobs there. We've got this guy. Who's he? This guy begins with GCCAC and GCCTT and other types of things there.

And this is the cross, so if we go now to Figure 3, this is the cross correlation of all those, and it holds the count. So you can see here 1, 1-- most of these are just 1. 1-- and unless I did some kind of thresholding, I probably couldn't even find the ones that were larger. And then figure 4 here is our pedigreed multiplication, so now it shows you what the actual. So this tells us that this reference sequence ID and this sample sequence ID had a match at this 10-mer.

So we back here. And as we see, as I clicked on that, it printed out the full sequence. So if you wanted to ever just do a cut and paste and then put this in something else-- so, like, if I wanted to look at this row, I could then do A1, and that gives me that row.

And I can do other things. I could do sum that-- I could sum the columns up. That tells me there's 138 unique sequences in that sequence ID. So those types of things there. All right. I think we pretty much covered that.

And so now we'll go on to the next example. And I apologize, this takes a little bit longer to run because now I'm doing two things when I read in the data. I'm doing the same thing I did before in terms of [INAUDIBLE] I want 10-mers, then I'm going to read the data again at a slightly different function, and it's going to return two associative arrays. This associative array was the same as before, which showed us the actual counts-- how many times.

The next one gives us a concatenated list of the positions, so if it appears five times, it'll actually show us-- it'll hold that information-- a list of the five locations in the greater sequence, which then allows us to do those things I talked about before. So this takes a minute to do that. Probably with some optimization, I have no doubt that this could be made faster. And also with the video recording going on, we have a lot of pressure on this personal computer.

Just some additional information here in terms of the whose command, so we basically did whose A to show me all the different associative arrays I have, as you can see. And this tallies up the bytes that are associated. So our first associative array, as you saw, was about 700 kilobytes. And that basically adds up all the data stored and all the data structures inside it. Usually does a pretty good job of that, likewise. And you can see, there's a significant reduction in the total size of that.

And in this case, we didn't really add that much by adding the keys, so this is a very nice dataset for us to do our CatKeyMul on. There was no dense diagonal or anything like that to get in our way there, so that was a very useful thing to have. At least we're now onto the second read, so almost there.

And being able to click on the thing it actually printed out is because when we actually do the spy plot, in this case, it works out pretty well because our keys are relatively short, but we do truncate that. So if you have a row key or a column key that's very long, when we do the plots we truncate that, and then you would never actually know what the true full string was. I think we're just about finished there.

All right, so again, we read in the data, and now I wanted to make a degree distribution of the data. So just like we did our degree distributions earlier, there's a great way to get a sense of the overall statistics. So I took one, A1N, and the way I do that is I have the associative array, A1. If I do the ADJ or adjacency matrix, this basically just pops out the internal sparse matrix that's stored. And now I can do regular math on that.

And we happen to have this little built-in function called out degree, which essentially does, on the out direction, the appropriate sums and returns a sparse matrix which we can then plot in this log log form. So is the reference data. You see as this distribution here, which is very power law-like, although, as we saw in the earlier classes, unless we properly fit and bin this, we wouldn't really know if this was a power law or something like it. But probably our first order linear fit of a power law would be at least a good place to start, as it usually is with this data.

There's the other one. Would appear to be even more power law-like, but again, until we bin it, we don't really know what happens. When we start binning this stuff up here, maybe it will bow up in some way, maybe it won't. Probably it would. Probably it would look more like this.

A question for you, or a good question is I showed you that other dataset, and it didn't look like this. You saw a very almost log normal Gaussian distribution. It's the same data. It's still 10-mer type of data, and so the only difference is the size. And so when you have 10-mers, since you have four choices of letter, you essentially have 2 million total possible 10-mers.

So this data set-- in fact, we can count here, right? That's A1. If we do N and Z-- we only have 274,000 entries, so we're not fully sampling the 2 million possibilities here. In the other dataset, that database was actually 500 million entries. And so we're really fully sampling, and so basically what's happening is these guys are rare, they don't show up, and you're hitting them once, and eventually you begin to create this sort of more Gaussian distribution look, or bell curve look when you start fully sampling.

I don't know if that's generally true or not, but one could hypothesize that a lot of the data-- and this just a guess-- a lot of the data we see is power law because we're not fully sampling the total space that emerges, or that total space is growing at a rate as we sample it. So domain names-- we haven't fully sampled the entire space of domain names, and the name, and the set of domain names, and the unit continues to grow at a fairly significant rate. Now, maybe one day there will stop being the new domain names, and then when we start doing our sampling, maybe our distributions and domain names won't look so power law anymore, but more like a log normal distribution with a kind of bell shape. Just a hypothesis, but certainly many data we have don't do that.

Now, of course, the easiest way for me to change this is instead of doing 10-mers would be to do 20-mers. Now I've dramatically increased the space of possibilities, and so the odds of having just statistical matches start piling up are very, very low. So that is certainly something that people do, too. And in the case for the calculation we were doing, we just got lucky. We actually did not think 10-mer would be the right sampling for that data. We thought it would be a higher number like a 15-mer or a 20-mer, and it turns out the 10-mer was just actually spot on in terms of giving us this nice balance between sampling, but statistical power that we could eliminate more common occurrences.

All right, so we plotted the out degree again, a very useful technique. One should always understand the overall statistics of one's data. We're doing the same cross correlation here that we did before, except since in that previous dataset the value didn't store to the count-- that was a very fast read, and all the values were 1-- here we actually have a count. And so in this particular correlation, we don't care if well, this 10-mer appeared 10 times in this one sequence and appeared 3 times in this other sequence, and when we multiply them together we get a 30.

We're really more interested in, like, how many unique 1's did they each have? How many distinct 1's did we each have? So we use the double logi function to basically convert all our numbers back to just 0's and 1's, and then do that correlation again. And since the values don't matter when we do the CatKeyMul, we don't need to do that, and then we do the same correlation. And so here we are. We're finding the sequences that have a greater than 8 match here. Actually doing some fairly inside tricks here to do that.

You might ask, what is this put? So it's fairly clear what I'm doing here. I'm taking this count and I'm saying, please return the sub-associative array of all things with greater than a value of 8, or more than eight matches. All right, that's good. Then I'm flooring that and saying, make that all just 1's.

And then I'm doing this trick here, which is called PutVal, and I'm giving it this random string. So right now this is just an associative array without a value. When I put that thing in there, since all my things have a value of 1 and I'll have one string, it's now saying, you know what, I've just made all those values tilde. I'm like, why on earth would we do that?

Well, it's because when I AND them together, we have to decide what mathematically-- when we AND two associative arrays together, if you recall the lecture where we talk about these collision functions, we have to pick a collision function for the two strings. And this key stores this pedigreed list, which I really want to keep. And this just shows me which ones are the high match, and I don't really care about that.

Well, the default collision function, when in doubt, throughout d4m is min. So tilde is lexicographically after every other printable character in the alphabet. So when I do a min here, I'm just going to always return these values here. So there was only one entry greater than 8, and I ANDed them together. It then did a min of tilde with this whole string here, and it said, aha, C is less than tilde. I'm just going to give you the C, and so there we go on. So this is just a cute trick, but it's a way of using the collision function in the group theory that we talked about in earlier lectures to get a very nice just selecting the one that I want here.

And so that's what that does. And then there you can see of this sequence ID and this sequence ID, they had greater than eight matches, and this was the exact 10-mers that actually matched. And then we can go back before and look up those two sequences, compare them side by side in the original data, and then we see these were the actual positions here. And you would probably look at these-- well, what do we think here? Well, 137 and 138, that's 139, 140, 141, and then jumping all the way to 149. So looks like those guys are all part of one long group. But then 60 and 172 and 130 are probably isolated 10-mers.

And then over here what do we have? We have 111-- no, but we do have 119, 120, 121, 122, 123, so that's probably also a bigger group match. In fact, those all line up with this, except for the 149 year. Well, actually, no. Some of them match, some of the time. So they're each part of a larger piece, but they aren't contiguous with each other. And that's the kind of thing that people who do this then really look at. And, of course, a real match would be more like something with many more sequences. This is all just random randomness and things like that.

All right, so that's the demo. I want to thank you. And again, next week tell your friends who weren't here today that that is the one lecture. If you had to come to one lecture in this entire class-- I didn't tell you that at the beginning, you notice, because then you would have skipped the other seven. But no, what we've done before will really make that a lot easier. That's the real one, and you will then be able to go, when you leave that lecture, run all those examples on those test databases that we have there from your LO grid accounts, and have all that kind of fun.

And we really want to do that because we've released d4m on the web, we need people to test it. It's much better if you guys find the issues, and then we'll just make it better. And likewise, it's a step towards you guys actually using the technology for your actual application. So thank you very much.

Free Downloads

Video

• iTunes U (MP4 - 52MB)
• Internet Archive (MP4 - 52MB)

Caption

• English-US (SRT)