D4M Session 2 Demo

• Download English-US transcript (PDF)

The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high quality educational resources for free. To make a donation or to view additional materials from hundreds of MIT courses, visit MIT OpenCourseWare at ocw.mit.edu.

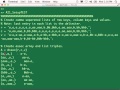
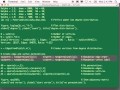
PROFESSOR: So again, we go here back up to the Examples, Intro, Group Theory, start it up. And then our first example is group theory 1, and it just goes through. And basically, I came up with a way in a spreadsheet to define the functions I was looking at, and then start creating combinations of them, and then do very simple tests on associativity and [? distribution ?] and all that stuff. If you actually look at the tests I do, you might blanch and be like, really? You said that? You declared that it was fully associative?

It's not like I went in and did formal proofs for everything. I just did some very quick numerical tests. The semi-ring test actually takes a while here, as you can see. And this will take a minute here. It appears to be hanging. Oh, no, it's not. Good. We'll let it go through that.

In fact, while it does that, we can look at-- basically, these are inputs. So basically, I have my different-- what I call the key function. I have union and intersection, and then I have the three possible conditions-- v1 less than v2, v1 equal to v2, v1 greater than v2, and then essentially, the different types of operators, the results that can occur from those.

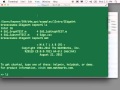
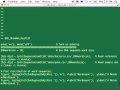
And so this is a CSV file, and we read it in as [? associative ?] [INAUDIBLE]. And so it looks like a spreadsheet, and I can actually have columns named v1 less than v1. Very powerful. And in fact, I'm even able to pass that column into the Matlab Eval function and have it actually execute it, which is nice. So I can actually have code in my column or row names, and then have operations performed based on that, which is, I think, a nice thing that you can do when you allow strings to be in your set. Likewise, Matlab will formally parse nan as nan and plus minus inf as minus inf, and so I can get all that functionality out of there, which is very nice.

And then it goes through-- let's see here. And these are just different tests that we do on those.

STUDENT: Is nan a special character?

PROFESSOR: Not a number. Yeah, I kind of-- I use that as-- it has a lot of the properties of null when you add it to different functions. So I'm using that for that, and it works out pretty well. So it's IEEE failure state modes or whatever it's-- it appears like that. I can't remember if there is a plus nan and negative nan as well. No. It's just nan, yeah.

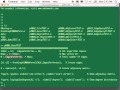
And then actually, it goes through here, and I think-- these are just various ways of inputting-- these are different values, different little spreadsheets that you can make for exploring these different types of things. And you can just write them as little CSV files. Very useful. On Instruct here. I do apologize for the length of time it's taking. I think having the QuickTime video recording going at the same time is causing the poor computer to sweat a little bit more than it does normally. It usually doesn't take this long.

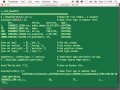
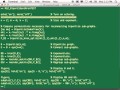
Outputs that it comes up with-- it basically writes all these out. Look here. This shows-- I ask it to basically generate all those 200 pairs. So for each key and whatever, it can go and generate those for me. So I create this little thing, and it goes through and creates this whole function, and then writes that out as a CSV itself, which is very convenient. Again, these are things you can do. I think this is the one where we came up with all the [? fields. ?] Oh, yeah. It doesn't really fit there. But you can see these are the pairs that it found, and it shows this is the zero operator. And again, this is all done with D4M kinds of values that it can store different types of things. This is how we made all the tables that are in there.

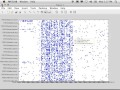
Oh, it's writing out results. That means it's done. There we go. And so the main one I want to show you is that we [? read in ?] that function, func range, and we permuted it. And if we do display full afunc, you can see there is the full combination of values as we saw there. So there's really nothing here for you. It's not I expect you to go using D4M to do group theory things. That's not really the point of these examples. I did. It's more just showing that you can-- when you go into this larger space, problems that you might not solve linear algebraically, all the sudden, it's like, oh yeah, if I have strings and other types of things, it really opens up the flexibility. I thought that was very neat that you could do this. It just handled the data very nicely and without any real difficulty.

So with that, that's the end of this lecture. I don't know if there's any final questions before we proceed. All right. Very good. And please, if you haven't signed up on the sheet, please do so. Thank you very much.

Free Downloads

Video

• iTunes U (MP4 - 19MB)
• Internet Archive (MP4 - 19MB)

Caption

• English-US (SRT)