D4M Session 1 Demo

• Download English-US transcript (PDF)

The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high quality educational resources for free. To make a donation or to view additional materials from hundreds of MIT courses, visit MIT OpenCourseWare at ocw.mit.edu.

PROFESSOR: All right. All right. So we're going to continue now and kind of get into the examples part of the course. And again, this is really the part that people should really-- I strongly encourage people doing examples. How many people got a chance to try the examples in the-- very good.

And we got a couple of questions for people. And most of the time we got another e-mail from them right away that said, no, got it to work. So we're very pleased about that. The great thing about working at Lincoln Labs is people are pretty good at figuring stuff out.

We have some experience this and before. Obviously, our parallel MATLAB technology, we've release that out. Many, many people use it. And for the most part, we're proud to say that whenever we get a question from the outside world, and it's not working, it's usually the person hasn't taken severely active steps to ignore the documentation. But if they follow it at all, they're generally pretty safe.

So I'm going to get into the example code here. So the example code this is-- oh, that's not, D4Muser_share, that's incorrect. It's tools lower case examples. I should correct these slides. Oh, nice. There we go. Great. That is an x, right? I hope so. Oh yes, thank you. Great. All right.

So this is where the example code is. We're going to go over here. Your assignment, should you choose to undertake it, is to pick a picture, hopefully something that's interesting to you. Doesn't have to be straight lines, it could be anything where you could create, draw edges, or something, you could take some photo and put it through one of those Photoshop effects and turn it into a line drawing or something and then start labeling vertices.

You do want to limit the number of lines though. I would recommend 20 would be the most number of lines you do. Because this can get fairly involved. You might start with something fairly small. So select a picture. Label the edges and vertices. Create an incidence matrix. And then just compute the adjacency matrix from the instance matrix using this formula.

You can certainly use d4m if you want to do that. But it's fine to do it by hand. It's fine to do it by hand, in which case you'd want to a very small one. Doing it once by hand is useful. Twice marginally. And then the third time, not useful. Just like in high school, right? They make you do matrix multiplied by hand like actually a lot. A lot.

So that's the example in the assignment. If you do this on a piece of paper and scan it and email it to me before the next lecture, I will give you some feedback on it before the following lecture. If you give it to me after that too bad. I just won't give you feedback. So there's no credit.

But this gives you some incentive to get it done. If you want feedback from me about what you did makes sense or if you encountered like I picked this picture and now I don't understand-- I did my best but I have questions about how I did this. Does it make sense? I'd be happy to do that. So just scan it, email it to me, or if it is electronic format you can do that as well.

So the lecture portion and now go back here. And let's see here, we go to examples. All right. So we're in the intro, EdgeArt directory, start my MATLAB shell. MATLAB. This takes about 15 seconds for it to do this.

This particular thing always CDs me to the location of the directory. You need to do that in order to see the examples. I think most MATLAB users are familiar with that. But just some that are not. Here is the actual adjacency matrix of that painting. So there it is. Same thing we just saw. So this is the data set that we're going to work with here.

So I'm going to do EA1. Again, all the examples are numbered in order, kind of that you're supposed to proceed through them. And if see a file in a directory that's like couple capital letters, which are the first two letters of the directory or the abbreviation of the directory in a test, that is the examples. The other files are just supporting files. You are not expected to run those. You can try running them but they'll probably cause you problems if you run them by themselves.

All right, here we go. So we just ran that example. Let's see what we got. I think that worked. So the first thing we did here is we read in our data. So we have this Read CSV, very useful function. Not necessarily the fastest.

In some of the later examples we have a sort of a super fast reader, which does almost no formatting for you. Just reads in the triples as raw triples. Because a lot of times if you're reading a very large CSV file, you may not want to construct the full associative array out of the way we would just do it by default. And you can just read in the triples very quickly then do some manipulations. Or a lot of times the first thing you'll do is recreate an associated array and then get the triples out of it, because you want to work on the triples directly. And so we do have ways for doing that.

So we now created the incidence matrix into an associative array. And let me just show you that. So if I go disp(E), so that shows you the incidence matrix. These are its internal structures here. These are the row keys. So those are the labels of the edges. They have been converted to Luxor graphically sorted order. We have the column keys. But there's so many that MATLAB chooses not to print out the full list here. But it's again, a Luxor graphically sorted list of the unique labels.

These are the different values that we have. So you remember we had an order column, which is one, two, three, blue, green, orange, pink, silver, etc. And here and then the overall adjacency matrix, which connects the row keys to their value keys is 19 by 21. 19 rows by 21 columns. This actually shows a mixed use.

Some of these are essentially exploded, right? The fact that we have each edge. But some of the values are actually storing real stuff here. Blue, green, orange, etc. So you don't have to go all the way with one. You can mix them too around. You can create dense matrices that look more like traditional tables. And there's sometimes that you want to do that. And other times you can completely explode it out and do things like that as well.

So we go back. We just want to work with the vertices. So we're going to ignore this color and order columns. So we're going to create our first projection is to just work with the vertices. So we have this little shorthand here called StartsWith, if you give it a character. And it will create a little query that will get just things that start with that. And very useful thing. It's very efficient too. It actually formally creates the two boundaries. It figures out what the maximum range is for that.

And then just needs to look up the beginning and the end. It [? can ?] [? assume ?] lexicographical order and then it can just grab the middle. We have a regular expression approach to it, which works fine on small associative arrays. But this is much more efficient because it's just basically two lookups and go. It also works if this E was actually a binding to a table in a database. You can use this same syntax, while the regular expression syntax doesn't really work. Yes?

[INAUDIBLE].

PROFESSOR: So that's the delimiter of the string. It's a string list with one entry in it. So this is a string list. All our strings are lists here. Well, because this also allows me-- could've been anything that was unique to that. And it didn't have to be the same delimiter that was the one inside. It could have been a new line, could have been a tab, could move whatever. I just picked comma because it was convenient but could have been a space. Because you could have multiple arguments to the StartsWith.

If you want to say I want starts with this and starts with this and starts with this, you just give it a whole list and it will go and do that all for you. And so that's why we do it that way. Wherever possible, we try and accept a list of strings. And then do the right thing.

So basically, this is saying, get me all columns that start with V. So that would be all the vertices. And this is the colon, which as you know and I want the full row of that. These had these values of-- which were the order group that they were in. And so we don't care about those. We want to convert them back to regular numeric numbers.

And so we have this shorthand here called double Logi, which basically just takes the logical and then does the double thing mathematically. Formally, you would use to call this the infinity norm on strings, if that even makes sense. But it basically just says, if there's a value there converted to a double precision one. If there's not a value there, it's just a sparse 0, not--

And we do this all the time because a lot of times we want to do math on these things. It's like regular math. We want to compute the vertex adjacency graph. So we do that with our square in function here, our inner square product. So that basically takes our matrix and uses the edge as the common key to join them together.

And we use or display full function to actually show what we got. And so now you see the vertex adjacency matrix here. And then the number is the number of times those vertices are on the same edge. So it's obviously symmetric. And you see here these vertices here, which are part of this common hyper edge, we have this sort of 6 9 6 structure here, various other types of symmetric structures going on here showing you the counts, how many times those vertices appeared on the same edge.

These are obviously cliques, because they are all vertices that are on the same hyper edge line. So if you have the same hyper edge line whenever you do the squaring operation, you see it as this clique in this operation here.

We can also do the square out function, which computes the edge adjacency matrix. So now we want to ask, which edges share common vertices? And so that's this structure here. It shows you these are the various edges. And again, it's symmetric. And you can see all kinds of structures in here about which vertices share-- which edges share common vertices.

And that is pretty much it for this example. Very simple example. Hopefully it gets you to the point where you can begin to try out the homework assignment. And if there's any questions that people have, let's try this. Here, one thing that's fun to do spy(E). See if that works.

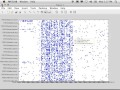
I think between PowerPoint, Quick Time and everything else it's just about-- there it is. Wow, that took a long time. So this shows that adjacency matrix. So spy works. And I don't know if we showed that in the first example, but the spy function, the standard MATLAB sparse plotting function, very useful way to just sort of look at the stuff, all those previous charts I showed you on the examples were done this thing.

And a little feature that sometimes causes MATLAB to crash because it doesn't really like doing things too aggressively. But if you click on it, it shows you the row and the column and the value associated with that, and also prints it out here. Likewise here. So you see row, column, that gives you the order. And this tells you the row is G2, its column, its color, its value is green.

So actually, I lied to you. That was just the first example. Senior moment there. We have two more to go. Lot more fun. See, you're all excited that class ended early.

Here's the other examples. So again, what we do is we're reading in the data set. We're displaying the full thing. So you can see there's the full beast I just showed you the spy plot. Now, I'm going to use some analytics on this. So one thing I want to do is just get the orange edges.

So I can say, get me the column color. And because orange is held in the value, I can actually compare it with the string. So I say, return me the matrix, the associative array of the row, color and everything equal to orange. So that returns me another associative array. The result of this whole logical expression is another associative array.

I can then get the rows for those associative arrays. And I've found all edges that are orange. And I can then pass that, get those rows and pass that back into the original one to get just the orange edges. So this just shows you this composable ability is very powerful, same ability that MATLAB has. One does similar statements in MATLAB all the time. And so it's very composable. This would be a very complex query to do in other approaches. And you can do it very quickly here. Yes? Question?

[INAUDIBLE] would that be called to route since it is in the row with the argument [INAUDIBLE]?

No. It doesn't. It doesn't. What we could do is overload it so if you passed an associative array with just a single argument and have it behave like when you pass in the MATLAB logical and do that kind of intersection, we could think about that. But MATLAB actually relies on then converting the matrix to a vector and then using that singular-- basically, it takes that logical, converts it to a single [? index, ?] which kind of gets us into an area where it's very fuzzy and gray.

So we definitely thought about that and there are places where we line up with MATLAB very nicely because the mathematics of associative arrays and linear algebra really line up very nicely. And there's places where they intersect. There's things you can do in with associative arrays that you can't do with linear algebra.

For example, we can matrix multiply any two associative arrays. There's no conformance requirements. That is, they don't have the same-- normally, when you multiply two matrices-- the inner dimensions have to match, basically. The columns of the left argument and the rows of the right argument must be the same length. In associative arrays that requirement doesn't exist. You can multiply or add any two associative arrays. We'll get into that much more in the next class. But that's a very powerful feature that people like.

But there's other places where it doesn't really make sense. So things like, what is the upper triangular section of an associative array gets to be a little bit-- huh, what's that mean? So excellent question though. Excellent question though.

So we can display this. So this just shows we found all the edges that had color orange. But we don't have to just-- that's a way of using the values to select. We could, of course, use StartsWith in the rows, just say StartsWith O and G. I just happened to label all my rows that orange rows began with O and green rows begin with G.

So we can do StartsWith O G. So that's example of those two range queries being done at the same time. And so that gives us EOG. And again, we can see now we get the orange and green rows. So that just shows you that.

And then we'll wrap up here with the last example, which is EA3. Now, we get to do some really fun stuff. Again, we're reading in our data set, converting, just getting the vertices. And then converting it to numeric 0's and 1's. I'm going to now just get the orange edges. And I'm going to get the green edges. All right. And now I'm going to essentially do the cross correlation of the orange and green edges.

So I'm going to transpose one of them and matrix multiply with the other ones. We don't do square in here because they' are different matrices. In fact, I would say that people often do the cross-correlation more often than just square the matrix with itself. You have one set with another set and you want to cross correlate them, a very common operation. And so that's just transpose EVG here. And that gets that.

And as you can see, the results of that inner product was empty. But the result of the outer product is full. So you guys can think about why that is. And so this just shows you the common-- how many edges these appeared with together. This shows you that there was no-- well, you guys can figure that out. I'll let you do your homework.

Now, another thing that we often want to do is basically, this showed us which edges had common shared vertices together. But it didn't tell us we lost the actual vertices. We just know that there's three. And a lot of times we want them. This is sometimes called the pedigree. You do a correlation. And then you would like-- you say these two things are correlated. I want to get to the connector back to the original record so I can go back to my e-matrix and really find that out and present that as the evidence that these things are connected together. We don't want to lose that.

So we have invented special new matrix multiplies in the land of associative arrays. One of them we call a CatKeyMul, which you view the matrix multiply as sort of there's a key, a common key, this row column key that's being joined together. Well, we can preserve that and store that in a value, instead of say the count or something like that.

So we do CatKeyMul EV0 transpose EVG. And then when we display that, we not only see which edges were connected, but we also have preserved the list of the vertices. It's essentially a concatenated list of those keys, very useful thing.

One has to be so very powerful technique. One definitely has to be careful about using this technique if it generates. It's going to generate extremely, extremely long lists here. That can really cause us to behave very slowly. In particular, when asked to be careful, if you do a CatKeyMul on a matrix with itself, why do you think you would have to be careful with that? Anyone?

Remember, that dense diagonal that happened whenever we squared matrices? So that means this thing will have an enormous number of entries along the diagonal. So you have to be very careful when you use this kind of function to correlate something with itself. It's better to correlate two distinct sets because they tend to not have that dense diagonal, which can be a little bit of a problem.

There's ways to get around that. There's hacks and tricks and stuff like that. But at a certain level, really dense diagonala-- I mean, essentially be listing every single vertex in your data set-- you could be listing every single vertex in your data set almost every single time, multiple times along the diagonal. That would get very, very bulky. So just a little word of caution there.

And so now, I've baited you once. But this really is the end. So are there any questions on the examples before we cut it off here? Is there a question back here somewhere? No? All right. Great. Thank you very much. I appreciate it. And we'll see you next week. And again, think of a picture, draw some lines, make an incidence matrix, have fun with it, compute the degree of your significant other. Bad idea? Good.

Free Downloads

Video

• iTunes U (MP4 - 54MB)
• Internet Archive (MP4 - 54MB)

Caption

• English-US (SRT)