D4M Session 3 Demo

• Download English-US transcript (PDF)

The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high quality educational resources for free. To make a donation, or to view additional materials from hundreds of MIT courses, visit MIT OpenCourseWare at ocw.mit.edu.

JEREMY KEPNER: Welcome back. We're now going get in the demo portion of lecture zero three. And so these demos are in the program directory, and the examples. We've now moved on from kind of the intro in to the applications, and we're going to do this when we're dealing with entities extracted from this data set.

So we go in to the entity analysis directory. Start my shell here, so. Start our MATLAB session here. I always run MATLAB from the shell. If you prefer to run it from the ID, that's fine. And again, our D4M code runs in a variety of environments, not just MATLAB. Right. That's started up here, so let's-- before we do that, let's look at our data set here.

So this is a nice little data set. It's about 2.4 megabytes of data. And some of the Reuters documents processed through our entity extractor here at Lincoln Laboratory. And so if I look at this, say with Microsoft Excel, try that.

All right, so you can see that pretty clearly, right? So we basically just have a row, key here to read this in. We have a document column, which is the actual-- so we widen that. That's the actual document that it appears in. We have the entity, happen to be alphabetical here, the way it comes out.

We have the word position in the document, so this tells you that this entity appeared in these positions in this document. And then various types-- location, person, organization, those types of things. So that's what we extracted from these documents. There's no verbs here.

We just tell you a person, a place, an organization, appeared in this document. It wouldn't say thing about what they're doing, or anything like that. So. But this just shows an example of the kind of data that we have here. So. There's that. To save. So, all right. So the first thing we're going to do, is the first script, is entity analysis one.

We're going to read the data in. All right, there we go. So-- and this first line just reads this in. We have-- it's a fair amount of data. We're turning it all in to an associative array. We have actually some faster parsers that will read it in. You know, but just the read CSV is kind of the most general purpose one that's fairly nice.

So it's going to go, and we'll go back. It's running about a whole bunch of stuff here. It tries to pull together its graphics. All right. So let's take a look at what we did here. So we read in the data into, essentially an edge list, associative array. Just display the first few rows here so you can see. So it's alphabetized.

The lexigraph we sorted the first columns, always something to be aware of. That 1 is then followed by 10, is then followed by 100 and then 1,000 in this sorting. Here's the documents, here's the entity. There's the positions. So it just looks like the normal table that we read in, but it is an associative array.

Now I'm going to want to sort of pull this into our exploded schema. And this table didn't necessarily come to us in the easiest format to do that in. So there's a few tricks that we have to do. So we're going to go and get each document, basically. So we have a row, a column and the doc, so that's the value.

So this is-- whenever you do a query in an associative array, one of the powerful things about MATLAB is you can change, you can have variable numbers of output arguments. And you can change the behavior. So if I just wanted this to return-- if I set this to, a equals e this, I would have just gotten an associative array vector.

But if I give it three output arguments, so say, I'll give you the triples that went into constructing that. Because sometimes that's what you want to do. Also it's faster, because to do this every time I do a sub associative array, I effectively have to pull out the triples, and then reconstitute the associative array.

And that could take some time. It just saves you a step. It goes directly to the triple switches, which is nice. So I basically say, give me the document column, give me the entity column, give me the position column. Now I have all these. And since I know they're dense, I know that these are all lined up.

The first doc string, and entity string, and position string, and type string are all-- so that's me exploiting a little bit. I know this is a dense table and I'm not going have any missing there. Now I'm going to interleave the type and entity strings. So I have this function called Cat String.

So basically Cat String takes one string list and another string list, and then it leaves them with a separator, a single character separator. And now I can construct a new sparse matrix, which has docks for the row key. This new thing called type entity, to be the columns, and I'll just throw the position in as the value.

And so that is our exploded schema that we just talked about. Done for us in a couple lines. There's other functions they do that as well. And since I don't want to repeat this, because it took a little while to read it in. I'm just going to save it as a MATLAB of binary, which will then read in very quickly from now on. Which is nice. So I can save it. There you go.

Just to show you, if I show you the first entry here, in the row. And then, this just shows you this is the different types of columns that were in that data set. So this the row key here. And the various columns. These are the different columns.

And then it shows you how many-- the locations of that word there. If I display it, I see that I ended up creating an associative array. And it consisted of almost 10,000 unique documents. And 3,657 unique entities in that data set. And then we're going to take a look at that. We can do spy and transpose.

If we look at here, zoom in on that. You can see different types of structures here. Click on one of them. And that tells us that the location Singapore appeared in this document in these two word positions. So. That's typically about how many lines it takes to take essentially a basic CSV file, and cast it into the associative array to start doing start doing real work.

That's typically what we see. If you find it's getting a lot longer than that, then that probably means there's a trick that you're not quite getting. And there again, we're always happy to help people do this very important step. This first-- taking your data and getting into this format so that you can do subsequent analysis on it.

All right. So there's that. Let's go on to the next sample here. So we're going to do some statistics on this. See, that took a lot less time loading it in from a binary much, much faster. Much, much faster. Very fast. I mean, faster than if you put in a database and read it out of a database. Much faster to read a file.

So we always encourage people to do that. This just gets displaced the size. So we have-- that's what we had in the original data. nnz shows the number of entries. So we do nnz, that's the number of entries. All right. I now want to undo what I did before.

I want to convert it back into a dense table. I want to take all those values, and convert-- I want to take all those things that [INAUDIBLE] because I just want to count how many, I want to know how many locations organization people have. So we have this function here called call-to-type.

And another function that I forget the precise name that does the reverse, which basically give me an associative array. Give me a delimiter for the columns, and I'm going to now rip that back apart. Stick that back into the value position, and then you're going to now sort of essentially make it dense again.

And so we do that. We then throw away the actual values. And so we do this double [INAUDIBLE], which converts it all to ones, and then we can sum the rows. So we collapsed along rows. Now we have count. It tells me in this data set I have 9,600 locations, organizations, people, time.

Those are the distinct ones there. All right. Let's see we can count each entity. So we have our thing here. We just do a count. We can find the triples-- so basically I've just done a sum. So this is the original, exploded scheme. I basically summed all the rows together. So now we're getting a count for each unique entity.

And I can find-- instead if one another way to get the triple is just to pass, use the find command. Works the same way as it does in MATLAB. It will now give you a set up of triples. A temp, which we don't really care about, because we've collapsed that dimensional to be all ones. The actual entity and the count.

And I'm going to create a new associative matrix out of that. So we now have the counts and the entity. And I'm going to plot a histogram of that. So I'm going to go with my count things. I'm just going to dip the locations out of that. So using that Starts With command, I say get me all locations.

I'm now going to just real map, and I say give me the adjacency matrix, which is return to regular sparse matrix. I can do sum, full, log, log. Now this is the classic degree distribution of all the locations in this data. And it shows us that certain locations are very common. A few of them are very common.

And a few locate, as they appear in most of the documents, and a lot of locations only appear in one document. So this is the classical-- we call power law-- degree distribution. Again, always a good thing to check. Sometimes you can't do this on the full data set, it's so large. But just even a sample, just to sort of-- you want to know this from the beginning.

Am I dealing with something that looks like a power law? So like everything else-- or oh, what do you know, I see a big spike here. Well what's that about? Or it looks like a bell curve. Or something like that. And so this is just really computing means, good. Computing basic histograms, very good.

Without this basic information, it's really hard to advance in detection theory. And so-- and this is probably where we take a slightly different philosophical approach than a lot of the data mining community, which tends to focus on just finding stuff that's interesting.

Where we tend to focus on understanding the data, modeling the data, coming up with models for what we're trying to find, and then doing that. Rather than just-- show me something interesting in the data. Show me a low probability covariance or something like that. Which tends to be more than the basis of the data mining community.

Although, no doubt, I probably offended them horribly by simplifying it that way. In which, case I apologize to people in the [INAUDIBLE] community. But here, we-- more traditional detection theory, and the first thing you want to do is get the distribution. So you can-- typically one thing you'll do immediately is like you know what, you put essentially what we call low pass, high pass filter on it.

Things that only appear once, or so unique that they give us no information, and things that appear everywhere again give us no information about the data. So you might just you have a high pass and a low pass filter that just sort of eliminates these high end and low end types of things. Very standard. Signal processing technique, that's just as relevant here as elsewhere.

All right. So statistics, histograms, all good things, easy to do in D4M on our data. Don't be afraid to take your data, bump it back into regular map of arrays, and just do the regular things that you would do it with

MATLAB data. With MATLAB matrices, we highly encourage that. Now we're going to do the facet algorithm that I talked about in the lecture. Let's do that. So once again, we've loaded our data in very quickly. We've decided to convert directly to numeric, which is-- we're getting rid of all those word positions, because we don't really care about them.

I'm going to pick-- so one thing I like about this data set, and for those of us who are a little older, we remember the news of the 1990's. You know? This is all a trip to remember [INAUDIBLE]. For those of you that are a little younger, who are in elementary school, this will not mean anything to you. But it's like-- oh yes.

A lot of stuff about the Clinton's in this data set. So that's always fun. So the first facet we're going to do is, we want to look at the location New York. And the person Michael Chang. Does anybody remember who Michael Chang was? Tennis player. Yes, he was kind of like this hip tennis player. Used to battle under Andre Agassi.

So, I don't know how long his career really lasted, but he was a very-- this is kind of right it his peak, I believe. So now there is-- to show you that equation that I showed you in the slides wasn't a lie. So we take our edge, or incidence matrix, we pick the column New York, then we then pick the column, Michael Chang.

We need to do this no call thing, because we now have a column vector with a column, Michael Chang. And a column New York. And if we enter them together, well they should have no intersections. So if we do know the no call, it just sort of pops those two column names away.

So now they're effectively both one, and we can add them together to find all the documents that contain both New York and Michael Chang. So we do that, so we've added them together. This is now a new column vector. OK. And we transpose it to make it a row vector. And then when we matrix multiply it back against the original data set.

We just computed the histogram of the other entities that are in the documents they contain both Michael Chang and New York. And as we can see, Michael Chang appears three times. That tells us there's three documents. And New York appears three times. But we also see Czech Republic, and Austria, and Spain, and the United States.

You want to guess why Czech Republic? Was Ivan Lendl still playing then? I'm just wandering if he had a lot of matches against him? Or would he already be into [INAUDIBLE] or something like that? I don't know. Probably had some Czech arch tribal or something like that. Or maybe there was just a tournament and these are the type of thing.

With the Reuters data sets, you do have the problem is that the person who types the article always puts the location where they filed it. So New York could always be in these just because the person happens to be based in New York, and typed it from New York or something like that. So that's always fun. We can normalize this.

So what I'm going to do is take the facets that we computed here, and normalize it by their sums. OK. So this just-- the facet is showing how many times something showed up, but it doesn't tell me if it's like-- well is that something that is really common or really rare.

So now we want to look at the places and things that were-- we want to see, of the other entities that appear in these documents, how many of them are really, really popular? And how many of them really just only appear in these documents with Michael Chang and New York.

So as you can see here-- so we have Belarus, Czech Republic, Virginia for some reason. And this just shows you-- look, these are in a lot of-- these have a very low, they're being divided by a fairly large number, which means they appear in a lot of places. So they happen to appear in the same set of documents.

But they happen to appear in a lot of documents. As opposed to Michael Joyce, or Virginia Wade. That's a tennis tournament, right? The Virginia Wade tennis tournament or something like that. These appear more common, or more likely, to be something that is like, oh that's a real sort of relation that exists between these entities.

So that just shows you how you do that. Again, very powerful. Very powerful technique. Basic covariance type of mat, so facets search is very powerful. All right, so I think we're now-- that was three, so we are moving on to four. So now we're going to do some stuff with graphs.

All kinds of graphs here, all kinds of graphs. So once again, we loaded in our data very quickly. We're just going to make a copy of it. And then I'm going to basically now convert the original thing to numbers. So get rid of those positions. And now we're going to do-- well so before, we did essentially the facets of the correlation between two things.

But the real power of D4M is it for about the same amount of work, we can correlate everything simultaneously. So we're going to do square in, which basically is the same as e transpose times e. It's a little bit faster when we're doing self correlations, but not too much. You could have typed e transpose times e.

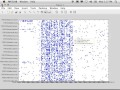
And then we're going to show the structure of that. So remember we had 3,657 unique entities. So now we've constructed a square matrix, it's 3,600 by 3,600 unique entities. And we're going to plot that. So let's see here. So that is-- hopefully this won't crash our computer.

So this is the location, by location-- this is the full entity-entity correlation matrix here. You can see all the structure. These are the locations. So this block here is location by location correlation. This block here is person-person correlation. It's obviously as a dense diagonal, it's symmetric.

And then down here are the time-time correlations. And so these in fact, the first thing you'll probably notice is these dense blocks of time have to deal with the fact that this is a finite set of Reuters documents. There's only 35 unique days, or times, associated with the documents themselves.

So those are showing you the times are associated with the-- reference. So that would be a very-- this type of structure shows, oh well if I want to just get the times that were associated with reporting, I can get that. Or if I want to do, the referring to some date.

And you can see there's times that are in the past, and future, and various types of things like that. And that shows you the structure. So this is a very nice structure. We can zoom in here. And then you see-- and more struct-- sub-structures emerge here. What's that one? Let me take a look. Here is this. United States, very popular-- dense.

You see that very dense thing, like the United States here. Who's this? This is probably America or something like that. United Nations Security Council, very popular. Oh-- the organizations here. Yeah, we don't have so many of them, it's the most popular. So you can just get this feel of the data, very powerful.

Because often, for the most part, when you work with your customer, and you do this, you can be just about 100% sure you're the first person to actually get a view. A high level view of the overall structure of the data, in a very powerful perspective. Because they simply just don't have a way to do this.

And using the sparse matrix is a way to just review the data. It's very, very powerful. All right. So let's get rid of that. So we did the entity-entity graph. Again, what we do is just whenever we take an incidence matrix, and we sort of square it, or correlate it.

Then the result is an adjacency matrix, or graph between those two things. So then adjacency matrices are a projection from the incidence matrix. We've lost some information, we've always thrown away some information in doing that.

But often, that's exactly what we want to do. You want to project it down into a subspace that we find more interesting. Something else that we can do, is let's just look at the people beginning with J.

All right. So I'm going to just get-- create a little starts with entity range here with our starts with command. I can pass that into it here, to grid just the records that have the entity p. And I'm going to do the correlation of them using this pedigree preserving matrix multiply that we have.

This very special one. So we'll go take a look at that. And that will explain what I mean by pedigree preserving. So we go here. So again, this shows you all the people that appear together, beginning with the name J. And it's of course again, symmetric matrix. Distance diagonal. You click on, it tells you.

So Jennifer Hurley and James Harvey appeared in this document together. So when we do that special matrix multiply, it doesn't preserve the values in the normal matrix multiply sense. Instead, it preserves the label of the common dimension that's eliminated. So when we do matrix multiply, you're limiting dimension.

We now take that common intersection and throw that in the value. So you can now say, Jennifer Hurley, James Harvey were connected by this document. And so very powerful tool for doing that. You notice, I restricted it to J. Why did I do-- why didn't just I do the whole thing? Well, you see this dense diagonal here.

If you had a very popular person, look at all the hits we're going to get when we correlated with itself. OK. This becomes a performance bottleneck when we start creating enormously long values. And so we always have to be careful when we do these pedigree preserving correlations.

If it's calculating one set with another, we're not have a dense diagonal. It's going to be fine. But if we're correlating something with itself, we always have to be on the lookout that we might be creating these dense diagonals. In which case, we could have an issue that we might create a very, very large value.

And the fact of the matter is, the way we sort the strains is we convert the list to a dense car matrix. And then call the MATLAB sort routine. It's the only way we can sort it. And so the width of that matrix is the length of the longest string in the list. So they're all about the same length, it's fine.

But if you have mostly things that are 20 characters, and then you have something that's 2,000 characters long. And you create 100,000 by 2,000 matrix, you've just consumed an awful lot of memory.

And sorting that and all that just-- so whenever people say it's slow or they run out of memory, it's almost always because they're creating, they have a string list and we're trying to manipulate it by sorting. And one of the values in that string is just extremely long. So that's just a little caveat.

A very powerful technique, you have to watch out for this diagonal. And there's ways to work around it, that are usually data specific. But again a very powerful-- this pedigree preserving correlation, something that usually people want. And especially since we almost usually store just like a one in the value, we're not really throwing away any information.

Sometimes we want it, because we want to count how many times those happen. If we didn't do the pedigree preserving, the catkey [INAUDIBLE], then we would have gotten a value of three here. And so we could have counted. It would have told us. Sometimes we do them both.

One that gives us the count, one that gives us the pedigree. And just store them both. There's different things that we want-- that we do with one versus the other. So again, having fun with the different types of matrix multiplies that we can do in the space of associative arrays. All right.

We're running out of time here, but I think we're almost done. So let me just see here. Then we did the document-document correlation, so this is the square out, which is e times e transpose. And we'll just take a quick look at that. So again, here we are for your four.

This just shows us which documents are closely related to each other. Which documents have a lot of common entities. So this just says here that these two documents share-- had one common entity with them. Other ones. Just clicking around here, not having a lot of luck finding one that's got a lot in it.

So maybe around here, nope. No. Well certainly if I click on the diagonal, nope. Wow. Basically pretty sparse, sparse correlations between these documents. So all right. And I think we'll go now to the last example. Is there a last example?

Yes. One-- one last one. Yay. [INAUDIBLE]. All right. So now we'll do-- the stuff I showed you so far is pretty easy stuff. Pretty sophisticated by a lot of the standards are out there, in terms being able to do sums, and histograms, and basic correlations.

That's often significantly beyond what is just sort of the run of the mill, which you'll just run in to if you just go into a place doing basic analysis. So again we load it. We convert everything to numeric. We've now squared it. So we created the graph. Now I want to get rid of that annoying diagonal, so I got the diagonal out.

So just so you know, all I did is I take-- I know it's a square, so I can do certain things without worrying. So I can basically take the adjacency matrix, that just going to be a regular MATLAB sparse matrix. I can now do-- take the diagonal back.

And since it's a square, I can just take those two, subtract them from each other, and just insert it back in without any harm done. Knowing it's like look, I took a square adjacency matrix out, did some manipulation. Stuff it back in. The dimensions are the same. You know, it should be OK.

I might have an issue that I may have introduced an empty row, or an empty column, you know. Which could cause me a little problems. I'm now going to get the triples of that, because I want to normalize the values here. So I'm going to get the-- the diagonals showed me how many counts are in each document.

So I want to normalize any entities in a document because sometimes you'll get a document that's like, and here's a list of every single country that participated in this UN meeting. And it'll have a hundred and something countries. So a country appearing in that document is not such a big deal, because all the countries appear in that document.

So this allows us to do that. If we want to do a correlation, we take the actual value and then divide it by the minimum. The least documented would be the maximum number of hits you could get in the correlation. You can do multi-facet queries. So we want do location against all people.

And so here's a more complicated query which says, find me all people that appeared more than four times, and with a probability greater than 0.3, and with respect to the New York. So here's New York, and all these different people who are basically-- these are people that appeared with New York, and almost exclusively appeared with New York.

So. So John Kennedy, so this is his son that was still alive at that time. Was very popular in the news. And so let's focus on him. So let's get John Kennedy, let's get his neighborhood. So we can go into his-- get all the people other people who appeared in documents with John Kennedy, and we can plot that neighborhood, and you go here.

This is his neighborhood. There's John Kennedy. His rows and columns. And then these are all the other people that appeared with him. You see this dense row and column. And then these are what are called the triangles. So these are other people who appeared in documents together, you know.

So George Bush and Jim Wright appeared in a document together, but not necessarily with John Kennedy. And we can actually find those people by just doing this basic arithmetic here. And this shows us all the triangles, all the other people also appeared in documents together, who appeared with John Kennedy.

And so that's what you asked. So with that, we will-- we're running a little bit late here, so we will wrap it up. And again, encourage you to go into your code, and run these examples and try out. And this should give you the first sense really kind of working with some real data, and playing with stuff. So. Thank you very much.

Free Downloads

Video

• iTunes U (MP4 - 76MB)
• Internet Archive (MP4 - 76MB)

Caption

• English-US (SRT)