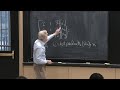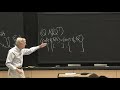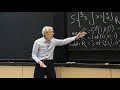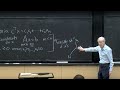Lecture 33: Neural Nets and the Learning Function

• Download English-US transcript (PDF)

The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high quality educational resources for free. To make a donation or to view additional materials from hundreds of MIT courses, visit MIT OpenCourseWare at ocw.mit.edu.

GILBERT STRANG: OK, so actually, I know where people are working on projects, and you're not responsible for any new material in the lectures. Thank you for coming. But I do have something, an important topic, which is a revised version about the construction of neural nets, the basic structure that we're working with. So that's on the open web at section 7.1, so Construction of Neural Nets. Really, it's a construction of the learning function, F.

So that's the function that you optimize by gradient descent or stochastic gradient descent, and you apply to the training data to minimize the loss. So I'm just thinking about it in a more organized way, because I wrote that section before I knew anything more than how to spell neural nets, but now I've thought about it more. So the key point maybe, compared to what I had in the past, is that I now think of this as a function of two sets of variables, x and v. So x are the weights, and v are the feature vectors, the sample feature vectors.

So those come from the training data, either one at a time, if we're doing stochastic gradient descent with mini-batch size 1. Or B at a time, if we're doing mini-batch of size B, or the whole thing, a whole epoch at once, if we're doing full-scale gradient descent. So those are the feature vectors, and these are the numbers in the linear steps, the weights. So they're the matrices AK that you multiply by, multiply v by. And also the bias vectors bK that you add on to shift the origin. OK.

It's these that you optimize, those are to optimize. And what's the structure of the whole of the learning function, and how do you use it? What does a neural net look like? So you take F of a first set of weights, so F of the first set of weights would be A1 and B1, so that's x part. And the actual sample vector, the sample vectors are v0 in the iteration.

And then you do the nonlinear step to each component, and that produces v1. So there is a typical-- I could write out what this is here, A1 v0 plus b1. The two steps are the linear step. The endpoint is v0. You take the linear step using the first weights, A1 and b1.

Then, you takes a nonlinear step, and that gives you v1. So that really better than my line above, so I'll erase that line above. Yeah. So that produces v1 from v0 and the first weights. And then the next level inputs v1, so I'll just call this vK or vK minus 1, and I'll call this one vK. OK, so K equal to 1 up to however many layers, you are l layers.

So the input was v0. So this v is really v0, you could say. And this is the neural net, and this is the input and output from each layer. And then vl is the final output from the final layer. So let's just do a picture here.

Here is v0, a sample vector, or if we're doing image processing, it's all the pixels in the data, in the training. From one sample, this is one training sample. And then you multiply by A1, and you add b1. And you take ReLU of that vector, and that gives you v1. That gives you v1, and then you iterate to finally vl, the last layer.

You don't do ReLU at the last layer, so it's just Al vl minus 1 plus bl. And you may not do a bias vector also at that layer, but you might, and this is the finally the output. So that picture is clearer for me than it was previously to distinguish between the weights.

So in the gradient descent algorithm, it's these x's that you're choosing. The v's are given by the training data. That's not part of the optimization part. It's x in chapter 6, where you're finding the optimal weights. So this x really stands for all the weights that you compute up to Al, bl, so that's a collection of all the weights.

And the important part for applications for practice is to realize that there are often more weights and more components in the weights than there are components in the feature vectors, in the samples, in the v's. So often, the size of x is greater than the size of v's which is an interesting and sort of unexpected situation. So often, I'll just write that.

Often, the x's are the weights. x's are underdetermined, because the number of x's exceeds, and often far exceeds, the number of v's, the number of the cardinality, the number of weights. This is in the A's and b's, and these are in the samples in the training set, the number of features of all the samples in the training set. So I'll get that new section 7.1 up hopefully this week on the open-- that's the open set-- and I'll email to you on Stellar.

Is there more I should say about this? You see here, I can draw the picture, but of course, a hand-drawn picture is far inferior to a machine-drawn picture an online picture, but let me just do it. So there is v, the training sample has some components, and then they're multiplied. Now, here is going to be v1, the first hidden layer, and that can have a different number of components in the first layer, a different number of neurons. And then each one comes from the v's-- so I will keep going here, but you see the picture.

So that describes a matrix A1 that tells you what the weights are on those, and then there's a b1 that's added. The bias vector is added to all those to get the v1. so v1 is A1 v0 plus b1, and then onwards. So this is the spot where drawing it by hand is clearly inferior to any other possible way to do it.

OK. So now, I haven't yet put into the picture the loss function. So that's the function that you want to minimize. So what is the loss function? So we're choosing x to-- that's all the A's and b's-- to minimize the loss, function L.

OK. So it's this part that Professor Sra's lecture was about. So he said, L is often a finite sum over all of F. So what would that be? F of x, vi, so this is the output from with weights in x from sample number i.

And if we're doing batch processing-- that is, we're doing the whole batch at once-- then we compute that for all i. And that's the computation that's ridiculously expensive, and you go instead to stochastic gradient. And you just choose one of those, or b of those, a small number b, like 32 or 128 of these F's. But full-scale gradient descent chooses the weights x to minimize the loss.

Now, so I haven't got the loss here yet. This function, the loss would be minus the true result from sample i. I haven't got a good notation for that. I'm open to suggestions.

So how do I want to write the error? So that would be-- if it was least squares, I would maybe be squaring that. So it would be a sum of squares of errors squared over all the samples. Or if I'm doing stochastic gradient descent, I would minimize. I guess I'm minimizing this.

But the question is, do I use the whole function L at each iteration, or do I just pick one, or only b, of the samples to look at iteration number K? So this is the L of x then. I've added up over all the v's. So just to keep the notation straight, I have this function of x and v's. I find it's output.

This is what the neural net produces. It's supposed to be close to the true. We don't want it to be exactly-- we don't expect this to be exactly 0, but it could be, because we have lots of weight to achieve that. So anyway, that would be the loss we minimize, and it'd be squared for square loss.

I guess I haven't really spoken about loss functions. Let me just put those here, and actually these are popular loss functions. One would be the one we know best, square loss, and number two, I've never seen it used quite this directly, would be the l1 loss, maybe the sum of L1 norms. This is sum of these errors squared in the L2 norm. The L1 loss could be the sum over i of the L1 losses.

Well, this comes into specific other problems like Lasso and other important problems you're minimizing an L1 norm but not in deep learning. Now, and three would be Hinge loss. Probably some of you know better than I the formula and the background behind hinge losses. This is for the minus 1, 1 classification problems. That would be appropriate for regression, so this would be for a regression.

And then finally, the most important for neural nets, is cross-entropy loss. This is for neural nets. So this is really the most used loss function in the setup that we are mostly thinking of, and I'll try to say more about that before the course ends. So is that-- I don't know. For me, I hadn't got this straight until rewriting that section, and it's now in better form, but comments are welcome. OK.

So that just completes what I wanted to say, and you'll see the new section. Any comment on that before I go to a different topic entirely? OK. Oh, any questions before I go to this topic? Which I'll tell you what it is. It's a short section in the book about distance matrices, and the question is.

We have a bunch of points in space, and what we know is we know the distances between the points, and it's convenient to talk about distances squared here. OK. And how would we know of these distances? Maybe by radar or any measurement. They might be sensors, which we've placed around, and we can measure the distances between them. And the question is, what's their position? So that's the question.

So let me talk a little bit about this question and then pause. Find positions in, well, in space, but I don't know. We don't know ahead of time maybe whether the space is ordinary 3D space, or whether these are sensors in a plane, or whether we have to go to higher dimensions. I'll just put d, and also, I'll just say then, we're also finding d.

And what are these positions? These are positions x, xi, so that the distance between xi minus xj squared is the given dij. So we're given distances between them, and we want to find their positions. So we know distances, and we want to find positions. That's the question.

It's just a neat math question that is solved, and you'll see a complete solution. And it has lots of applications, and it's just a nice question. So it occupies a section of the book, but that section is only two pages long. It's just a straightforward solution to that question. Given the distances, find the positions. Given the distances, find the excess.

OK. So I'm going to speak about that. I had a suggestion, a good suggestion, by email. Well, questions about the projects coming in? Projects are beginning to come in, and at least at the beginning-- well, in all cases, beginning and end, I'll read them carefully.

And as long as I can, I'll send back suggestions for a final rewrite, and as I said, a print out is great. You could leave it in the envelope outside my office, but of course, online is what everybody's doing. So those are just beginning to come in, and if we can get them in by a week from today, I'm really, really happy.

Yeah, and just feel free to email me. I would email me about projects, not Jonathan and not anonymous Stellar. I think you'd probably do better just to ask me the question. That's fine, and I'll try to answer in a useful way.

Yeah, and I'm always open to questions. So you could email me like how long should this project be? My tutor in Oxford said something like-- when you were writing essays. That's the Oxford system is to write an essay-- and he said, just start where it starts, and end when it finishes. So that's the idea, certainly not enormously long.

And then a question was raised-- and I can ask you if you are interested in that-- the question was, what courses after this one are natural to take to go forward? And I don't know how many of you are thinking to take, have time to take, other MIT courses in this area of deep learning, machine learning, optimization, all the topics we've had here. Anybody expecting to take more courses, just stick up a hand. Yeah, and you already know like what MIT offers? So that was the question that came to me, what does MIT offer in this direction?

And I haven't looked up to see the number of Professor Sra's course, S-R-A, in course 6. It's 6 point high number, and after his good lecture, I think that's got to be worthwhile. So I looked in course 6. I didn't find really an institute-wide list. Maybe course 6 feels that they are the Institute, but there are other courses around. But I found in the operations research site, ORC, the Operations Research Center, let me just put there. This is just in case you would like to think about any of these things.

As I write that, so I heard the lecture by Tim Berners-Lee. Did others hear that a week or so ago? He created the web. So that's pretty amazing-- it wasn't Al Gore, after all, and do you know his name?

Well, he's now Sir Tim Berners-Lee. So that double name makes you suspect that he's from England, and he is. So anyway, I was going to say, I hold him responsible for these excessive letters in the address, in the URL. I mean, he's made us all say W-W-W for years. Find some other way to say it, but it's not easy to say, I think.

OK, whatever. This is the OR Center at MIT, and then it's academics or something, and then it's something like course offerings. That's approximately right. And since they do applied optimization, under the heading of data analytics or statistics, there's optimization, there's OR, Operations Research, other lists but a good list of courses from many departments, especially course 6. Course 15 which is where the operation and research center is, course 18, and there are others in course 2 and elsewhere. Yeah.

Would somebody like to say what course you have in mind to take next, after this one? If you looked ahead to next year, any suggestions of what looks like a good course? I sat in once on 6.036, the really basic course, and you would want to go higher. OK.

Maybe this is just to say, I'd be interested to know what you do next, what your experience is, or I'd be happy to give advice. But maybe my general advice is that that's a useful list of courses. OK? Back to distance matrices. OK, so here's the problem. Yeah. OK, I'll probably have to erase that, but I'll leave it for a minute.

OK. So we know these distances, and we want to find the x's, so let's call this dij maybe. So we have a D matrix, and we want to find a position matrix, let me just see what notation. So this is section 3.9, no 4.9, previously 3.9, but chapters 3 and 4 got switched. Maybe actually, yeah, I think it's 8 or 9 or 10, other topics are trying to find their way in. OK. So that's the reference on the web, and I'll get these sections onto Stellar.

OK. So the question is, can we recover the positions from the distances? In fact, there's also a question, are there always positions from given distances? And I mentioned several applications. I've already spoken about wireless sensor networks, where you can measure travel times between them, between the sensors. And then that gives you the distances, and then you use this neat little bit of math to find the positions.

Well, of course, you can't find the positions uniquely. Clearly, you could any rigid motion of all the positions. If I have a set of positions, what am I going to call that, x? So I'll write here, and so I'm given the D matrix. That's distances, and the job is to find the X matrix which gives the positions.

And what I'm just going to say, and you already saw it your mind-- that if I have a set of positions, I could do a translation. The distances wouldn't change, or I could do a rigid motion, a rigid rotation. So positions are not unique, but I can come closer by saying, put the centroid at the origin, or something like that. That will take out the translations at least.

OK. So find the X matrix. That's the job. OK, and I was going to-- before I started on that-- the shapes of molecules is another application. Nuclear magnetic resonance gives distances, gives d, and then we find the positions x. And of course, there's a noise in there, and sometimes missing entries.

And machine learning could be just described also as you're given a whole lot of points in space, feature vectors in a high-dimensional space. Actually, this is a big deal. You're given a whole lot of points with in high-dimensional space, and those are related. They sort of come together naturally, so they tend to fit on a surface in high-dimensional space, a low-dimensional surface in high-dimensional space.

And really, a lot of mathematics is devoted to finding that low-dimensional, that subspace, but it could be curved. So subspace is not the correct word. Really, manifold, curved manifold is what a geometer would say. That is close to all the-- it's smooth and close to all the points, and you could linearize it. You could flatten it out, and then you have a much reduced problem.

The dimension is reduced from the original dimension of where the points lie with a lot of data to the true dimension of the problem which, of course, sets of points were all on a straight line. The true dimension of the problem would be 1. So we have to discover this. We also have to find that dimension d. OK, so how do we do it?

So it's a classical problem. It just has a neat answer. OK. All right, so let's recognize the connection between distances and positions. So dij is the square distance between them, so that is xi dot xi minus xi to xj minus xj, xi plus xj, xj. OK. Is that right? Yes.

OK. So those are the dij's in a matrix, and these are entries in the matrix D. OK. Well, these entries depend only on i. They're the same for every j. So this is going to be-- this will this part will produce-- I'll rank one matrix. Because things depend not only on the row but not on j, the column number, so columns repeated.

Yeah, and this produces similarly something that depends only on j, only on the column number. So the rows are all the same, so this is also a rank one matrix with all repeated, all the same rows. Because if I change i, nothing changes in a product. So really, these are the terms that produce most of the matrix, the significant part of the matrix.

OK. So what do we do with those? So let's see, did I give a name for the matrix that I'm looking for? I think in the notes I call it X. So I'm given D, find X.

And what I'll actually find-- you can see it coming here-- is actually find X transpose X. Because what I'm given is dot products of X's. So I would like to discover out of all this what xi dotted with xj is. That'll be the correct dot product. Let's call this matrix G for the dot product matrix, and then find X from G.

So this is a nice argument. So what this tells me is some information about dot products. So this is telling me something about the G matrix, the X transpose X matrix. And then once I know G, then it's a separate step to find X. And of course, this is the point at which X is not unique.

If I put it in a rotation into X, then that rotation q, I'll see a q transpose q, and it'll disappear. So I'm free to rotate the X's, because that doesn't change the dot product. So it's G that I want to know, and this tells me something about G, and this tells me something about G. And so does that, but that's what I have to see.

So what do those tell me? Let's see. Let me write down what I have here. So let's say a diagonal matrix with Dii as the inner product xi with xi that we're getting partial information from here.

So is that OK? I'm introducing that notation, because this is now going to tell me that my D matrix is-- so what is that? So this is the diagonal matrix. Maybe it's just a vector, I should say. Yeah. Yeah, so can I write down the equation that is fundamental here, and then we'll figure out what it means.

So it's an equation for G, for the dot product matrix. OK, let me make space for that equation. I believe that we can get the dot product matrix which I'm calling G as-- according to this, it's minus 1/2 of the D matrix plus 1/2 of the 1's times the d, the diagonal d. And it's plus 1/2 of the d times the 1's. That's a matrix with constant rows.

This here is coming from there. This is a matrix with always the same columns, or let me see. No, I haven't got those right yet. I mean, I want these to be rank 1 matrices, so it's this one. Let me fix that.

1, 1, 1, 1 times d transpose, so it's column times row, and this one is also column times row with the d here. OK, now let me look at that properly. So every row in this guy is a multiple of 1, 1, 1, 1. So what is that telling me? That all columns are the same, this part is reflecting these ones, where the columns are repeated.

This one is reflecting this, where the rows are repeated. The d is just the set of d numbers. Let's call that di, and this is dj, and here's the D matrix. So part of the D matrix is this bit and this bit, each giving a rank 1. Now, it's this part that I have to understand, so while you're checking on that, let me look again at this. Yeah.

Let's just see where we are if this is true. If this is true, I'm given the D matrix, and then these dot products I can find. So I can find these, so in other words, this is the key equation that tells me D. That's the key equation, and it's going to come just from that simple identity, just from checking each term. This term we identified, that last term we identified, and now this term is D. Well, of, course it's D.

So I have two of those, and I'm going to take half of that to get D, I think. Yeah, and we'll look. Yeah. So I guess I'm not seeing right away why this 1/2 is in here, but I think I had it right, and there's a reason. You see that this matrix this, X transpose X matrix, is coming from these rank 1 pieces and these pieces which are the cross product.

Oh, I see. I see. What that equation is really saying is that the D matrix is this-- if I just read that along and translate it and put it in matrix language-- is this 1, 1, 1, 1, d1 to d4, let's say, transpose is this rank 1 matrix. And the other one is the d's times the 1, 1 which is a transpose of that. And then the other one was a minus 2 of the cross product matrices. I see. Yeah.

So when I write that equation in matrix language, I just get that. And now, when I solve for X-- oh, minus 2 X transpose X. Yeah. Sorry, cross products, the X's. So I had one set of cross products, and then this is the same as this, so I have minus 2 of them. So now, I'm just rewriting that. When I rewrite that equation, I have that.

Do you see that? I put that on this side. I put the d over here as a minus d. I divide by 2, and then that's the formula. So ultimately, this simple identity just looked at-- because these pieces were so simple, just rank one pieces, and these pieces were exactly what we want, the X transpose X pieces, the G.

That equation told us the D. All this is known. Well, so what's known is D and this and this. So now, we have the equation for X transpose X is minus 1/2 of D minus these rank 1's.

Sorry to make it look messy. I remember Raj Rao talking about it last spring, also the algebra got flustered. So we get it. So we know X transpose X, that matrix.

Now, can we just do four minutes of linear algebra at the end today? Given X transpose X, find X. This is n by n. How would you do that? Could you do it?

Would there be just one X? No. So if you had one X, multiply that by a rotation, by an orthogonal matrix, you'd have another one. So this is finding X up to an orthogonal transformation, but how would you actually do that? What do we know about this matrix, X transpose X? It's symmetric, clearly, and what we especially know is that it is also?

AUDIENCE: Positive.

GILBERT STRANG: Positive or semidefinite, so this is semidefinite. So I'm given a semidefinite matrix, and I want to find a square root, you could say. That matrix is the X transpose X, and I want to find X. I think there are two leading candidates. There are many candidates, because if you find one, then any QX is OK. Because if I put a Q transpose Q in there, it's the identity.

OK. So one way is to use eigenvalues of X transpose X, and the other way would be to use elimination on X transpose X. So I'll put use. So if I use eigenvalues of X, if I find the eigenvalues of X transpose X, then I'm writing this a-- it's a symmetric, positive definition-- I'm writing it as Q lambda Q transpose. Right? That's the fundamental most important theorem in linear algebra, you could say. That a symmetric, positive, semidefinite matrix has greater eigenvalues, greater or equal to 0, and eigenvectors that are orthogonal.

So now, if I know that, what's a good X? Then, take X to be what? So I've got the eigenvalues and eigenvectors of X transpose X, and I'm looking for an X that will work. And one idea is just to take the same eigenvectors, and take the square roots of the eigenvalues.

That's symmetric now. This is equal to X transpose, and that's a square root symbol, or a lambda to the 1/2, I could say. So when I multiply that-- X transpose X is just X squared here. When I square it, the Q transpose Q multiplies itself to give the identity. The square root of lambda times the square root of lambda, those are diagonal matrices that give lambda, and I get the right answer.

So one way is, in a few words, take the square roots of the eigenvalues and keep the eigenvectors. So that's the eigenvalue construction. So that's producing an X that is symmetric, positive, semidefinite. That might be what you want. It's a little work, because your computing eigenvalues and eigenvectors to do it, but that's one choice.

Now, I believe that elimination would give us another choice. So elimination produces what factorization of this? This is still our symmetric, positive, definite matrix. If you do elimination on that, you usually expect L, a lower triangular, times D, the pivots, times U, the upper triangle. That's the usual result of elimination, LDU.

I'm factoring out the pivots, so they're 1's on the diagonals of L and U. But now, if it's a symmetric matrix, what's up? We zipped by elimination, regarding that as a 18.06 trivial bit of linear algebra, but of course, it's highly important.

So what's the situation here when the matrix is actually symmetric? So I want something to look symmetric. How do I make that look symmetric? The U gets replaced by L transpose. If I'm working on a positive definite-- say positive definite matrix-- then I get positive pivots, and L and lower triangular and upper triangular are transposes of each other.

So now, what is then the X? It's just like that. I'll use L square root of the D L transpose. Is that right? Oh, wait a minute. What's up?

No, that's not going to work, because I don't have L transpose L. Where I had Q transpose Q, it was good. No, sorry. Let's get that totally erased. The X part should just be the square root of DL transpose. The X is now a triangular matrix, the square root of the pivots, and the L transpose part.

And now, when I do X transpose X, then you see X transpose X coming correctly. X transpose will be L transpose. Transpose will give me the L. Square root of D will be square root of D. We'll give the D, and then the L transpose is right.

So this is called the-- do I try to write it here? This is my last word for today-- the Cholesky. This is the Cholesky Factorization, named after a French guy, a French soldier actually. So LDL transpose is Cholesky, and that's easy to compute, much faster to compute than the eigenvalue square root.

But this square root is triangular. This square root is symmetric. Those are the two pieces of linear algebra to find things, to reduce things to triangular form, or to reduce them to connect them with symmetric matrices.

OK, thank you for attention today. So today, we did the distance matrices, and this was the final step to get the X. And also, most important was to get the structure of a neural net straight, separating the v's, the sample vectors, from the x's, the weights.

OK, so Friday, I've got one volunteer to talk about a project, and I'm desperately looking for more. Please just send me an email. It'd would be appreciated, or I'll send you an email, if necessary. OK, thanks.

Problems for Lecture 33
From textbook Section VII.1

5. How many weights and biases are in a network with \(m=N_0=4\) inputs in each feature vector \(\boldsymbol{v}_0\) and \(N=6\) neurons on each of the 3 hidden layers? How many activation functions \((\hbox{ReLU})\) are in this network, before the final output?

From textbook Section IV.10

2. \(||\boldsymbol{x}_1-\boldsymbol{x}_2||^2=9\) and \(||\boldsymbol{x}_2-\boldsymbol{x}_3||^2=16\) and \(||\boldsymbol{x}_1-\boldsymbol{x}_3||^2=25\) do satisfy the triangle inequality \(3+4>5\). Construct \(G\) and find points \(\boldsymbol{x}_1,\boldsymbol{x}_2,\boldsymbol{x}_3\) that match these distances.

Free Downloads

Video

• Internet Archive (MP4 - 125MB)

Caption

• English-US (SRT)