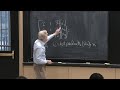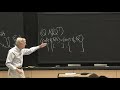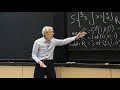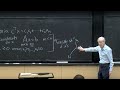Lecture 31: Eigenvectors of Circulant Matrices: Fourier Matrix

• Download English-US transcript (PDF)

NARRATOR: The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high-quality educational resources for free. To make a donation or to view additional materials from hundreds of MIT courses, visit MIT OpenCourseWare at ocw.mit.edu.

GILBERT STRANG: OK. So, I'd like to pick up again on this neat family of matrices, circulant matrices. But first, let me say here and then put it on the web, my thought about the projects. So, I think the last deadline I can give is the final class. So, I think that's not next week but Wednesday of the following week, I think, is our last class meeting.

So, be great to get them then or earlier. And if anybody or everybody would like to tell the class a little bit about their project, you know it's a friendly audience and I'd be happy to make space and time for that. So, send me an email and give me the project earlier if you would like to just say a few words in class. Or even if you are willing to say a few words in class, I'll say. Yeah. Because I realize-- yeah, OK. So, other questions about-- so, we're finished with all psets and so on. So, it's really just a project, and yeah.

STUDENT: How is the project graded? Like, on what basis?

GILBERT STRANG: How is it graded? Good question. But it's going to be me, I guess. So I'll read all the projects and come up with a grade somehow, you know.

I hope you guys have understood that my feeling is that the grades in this course are going to be on the high side because they should be. Yeah. I think it's that kind of a course and I've asked you to do a fair amount, and-- anyway, that's my starting basis.

And there's a lot of topics like circulant matrices that I'm not going to be able to give you a pset about. But of course, these are closely connected to the discrete Fourier transform. So, let me just write the name of the great man Fourier. So, the discrete Fourier transform is, as you know, a very, very important algorithm in engineering and in mathematics. Everywhere. Fourier is just a key idea and so I think it's just good to know about, though.

So, circulant matrices are connected with finite size matrices. Matrices of size n. So our circulant matrices will be N by N. And you remember this special form. So, this is a key point about these matrices, C. That they're defined by not n squared entries, only n.

If you tell me just the first row of the matrix, and that's all you would tell Matlab, say, c0, c1, c2 to c N minus 1. Then for a circulant, that's all I need to know because these diagonals are constant. This diagonal is constant-- c1-- and then gets completed here. c2 diagonal come to c2 and then gets completed cyclically here.

So, n numbers and not n squared. The reason I mention that, or a reason is, that's a big selling point when you go to applications, say machine learning, for images. So, you remember the big picture of machine learning, deep learning, was that you had samples. A lot of samples, let's say N samples, maybe.

And then each sample in this image part will be an image. So, the thing is that an image is described by its pixels and if I have 1,000 by 1,000 pixel-- so, that's a million pixels. The feature vector, the vector that's associated with 1 sample, is enormous. Is enormous. So I have N samples but maybe-- well, if they were in color that million suddenly becomes 3 million.

So say 3 million features. So, our vectors are a vector of-- the whole computation of deep learning works with our vectors with 3 million components. And that means that in the ordinary way, if we didn't do anything special we would be multiplying those by matrices of size like 3 million times 3 million.

We would be computing that many weights. That's like, impossible. And we would be computing that for each layer in the deep network so it would go up-- so 3 million by 3 million is just-- we can't compute. We can't use gradient descent to optimize that many weights.

So, the point is that the matrices in deep learning are special. And they don't depend-- they're like circulant matrices. They might not loop around. So, circulant matrices have this cyclic feature that makes the theory extremely nice. But of course, in general we have matrices, let's say t0-- constant diagonals and maybe a bunch of diagonals. And here not necessarily symmetric, or they might be symmetric. But they're not cyclic.

So, what are these matrices called? Well, they have a bunch of names because they're so important. They're linear shift invariant. Or linear time invariant, whatever is the right word in your context. So, they're convolutions. You could call it a convolution matrix.

When you multiply by one of these matrices, I guess I'm going to call it t, you're doing our convolution. And I'll better write down the formula for convolution. You're not doing a cyclic convolution unless the matrix cycles round. When you multiply by C, this would give you cyclic convolution.

Say if I multiply C by some vector v, the result is the cyclic convolution of the c vector with the v vector. So, big C is a matrix but it's completely defined by its first row or first column. So I just have a vector operation in there and it's a cyclic one. And over here, t times a vector v will be the convolution of a t vector with v, but not cyclic.

And probably these are the ones that would actually come into machine learning. So, linear shift invariant, linear time invariant. I would call it-- so, math people would call it a Toeplitz matrix. That's why I used the letter t. In engineering it would be a filter or a convolution or a constant diagonal matrix.

These come up in all sorts of places and they come up in machine learning and with image processing. But basically, because what you're doing at one point in an image is pretty much what you're going to do at the other points, you're not going to figure out special weights for each little pixel in the image.

You're going to take-- if you have an image, say you have an image with zillions of pixels. Well, you might want to cut down. I mean, it would be very sensible to do some max pooling, some pooling operation to make it smaller.

So, that's really like, OK, we don't want this large a system. Let's just reduce it. So, max pooling. That operation would be-- say, take them 3 at a time, some 9 pixels. And replace that 9 pixels by 1 pixel. So the max of those 9 numbers. That would be a very simple operation that just reduces the dimension, make it smaller. Reduce the dimension.

OK, so that's a cheap way to make an image 4 times or 9 times or 64 times smaller. But the convolution part now-- so, that's not involving convolution. That's a different operation here. Not even linear if I take the max in each box. That's not a linear operation but it's a fast one.

OK, so where do circulants or convolution or Toeplitz matrices or filters come into it? So, I'll forget about the max pooling. Suppose that's happened and I still have a very big system with n squared pixels, n squared features for each sample. So, I want to operate on that by matrices, as usual. I want to choose the weights to bring out the important points.

So, the whole idea is-- on a image like that I'll use a convolution. The same operation is happening at each point. So, forget the max part. Let me erase, if I can find an eraser here. OK, so I'm not going to-- we've done this. So, that's done.

Now, I want to multiply it by weights. So, that's already done. OK. So, what am I looking to do? What kind of a job would a filter do?

A low-pass filter would kill, or nearly kill, the high frequencies, the noise. So, if I wanted to get a simpler image there, I would use a low-pass filter, which might just-- it might be this filter here. Let me just put in some numbers that would-- say 1/2 and 1/2.

So, I'm averaging each pixel with its neighbor just to take out some of the high frequencies. The low frequencies are constant. An all-black image would come out not changed but a very highly speckled image would get largely removed by that averaging.

So, it's the same idea that comes up in all of signal processing, filtering. So, just to complete this thought of, why do neural nets-- so, I'm answering this question. How do they come in machine learning?

So, they come when the samples are images and then it's natural to use a constant diagonal matrix, a shift invariant matrix and not an arbitrary matrix. So, we only have to compute n weights and not n squared. Yeah, so that's the point. So, that's one reason for talking about convolution and circulant matrices in this course.

I guess I feel another reason is that everything to do with the DFT, with Fourier and Fourier transforms and Fourier matrices, that's just stuff you gotta know. Every time you're dealing with vectors where shifting the vectors comes into it, that's-- Fourier is going to come in.

So, it's just we should see Fourier. OK. So now I'll go back to this specially nice case where the matrix loops around. Where I have this cyclic convolution. So, this would be cyclic because of the looping around stuff.

So, what was the point of last time? I started with this permutation matrix. And the permutation matrix has c0 equals 0, c1 equal 1, and the rest of the c's are 0. So, it's just the effect of multiplying by this-- get a box around it here-- the effect of multiplying by this permutation matrix is to shift everything and then bring the last one up to the top. So, it's a cyclic shift.

And I guess at the very end of last time I was asking about its eigenvalues and its eigenvectors, so can we come to that question? So, that's the starting question for everything here. I guess we've understood that to get deeper into a matrix, its eigenvalues, eigenvectors, or singular value, singular vectors, are the way to go. Actually, what would be the singular values of that matrix?

Let's just think about singular values and then we'll see why it's eigenvalues we want. What are the singular values of a permutation matrix? They're all 1. All 1. That matrix is a orthogonal matrix, so the SVD of the matrix just has the permutation and then the identity is there for the sigma. So, sigma is I for this for this matrix.

So, the singular values don't-- that's because P transpose P is the identity matrix. Any time I have-- that's an orthogonal matrix, and anytime P transpose P is the identity, the singular values will be the eigenvalues of the identity. And they're all just 1's. The eigenvalues of P, that's what we want to find, so let's do that.

OK, eigenvalues of P. So, one way is to take P minus lambda I. That's just the way we teach in 18.06 and never use again. So, it puts minus lambda on the diagonal, and of course P is sitting up here. And then the rest is 0.

OK, so now following the 18.06 rule, I should take that determinant, right? And set it to 0. This is one of the very few occasions we can actually do it, so allow me to do it. So, what is the determinant of this? Well, there's that lambda to the fourth, and I guess I think it's lambda to the fourth minus 1. I think that's the right determinant.

That certainly has property-- so, I would set that to 0, then I would find that the eigenvalues for that will be 1 and minus 1, and I and minus I. And they're the fourth roots of 1. Lambda to the fourth equal 1. That's our eigenvalue equation. Lambda to the fourth equal 1 or lambda to the n-th equal 1.

So, what would be the eigenvalues for the P 8 by 8? This is the complex plane, of course. Real and imaginary. So, that's got 8 eigenvalues.

P to the eighth power would be the identity. And that means that lambda to the eighth power is 1 for the eigenvalues. And what are the 8 solutions? Every polynomial equation of degree 8 has got to have 8 solutions. That's Gauss's fundamental theorem of algebra.

8 solutions, so what are they? What are the 8 numbers whose eighth power gives 1? You all probably know them. So, they're 1, of course the eighth power of 1, the eighth power of minus 1, the eighth power of minus I, and the other guys are just here.

The roots of 1 are equally spaced around the circle. So, Fourier has come in. You know, Fourier wakes up when he sees that picture. Fourier is going to be here and it'll be in the eigenvectors. So, you're OK with the eigenvalues?

The eigenvalues of P will be-- we better give a name to this number. Let's see. I'm going to call that number w and it will be e to the 2 pi i over 8, right? Because the whole angle is 2 pi divided in 8 pieces. So that's 2 pi i over 8. 2 pi i over N for a matrix of-- for the n by n permutation.

Yeah, so that's number w. And of course, this guy is w squared. This one is w cubed, w fourth, w fifth, sixth, seventh, and w to the eighth is the same as 1. Right.

The reason I put those numbers up there is that they come into the eigenvectors as well as the eigenvalues. They are the eigenvalues, these 8 numbers. 1, 2, 3, 4, 5, 6, 7, 8 are the 8 eigenvalues of the matrix. Here's the 4 by 4 case. The matrix is an orthogonal matrix.

Oh, what does that tell us about the eigenvectors? The eigenvectors of an orthogonal matrix are orthogonal just like symmetric matrices. So, do you know that little list of matrices with orthogonal eigenvectors?

I'm going to call them q. So qi dotted qj, the inner product, is 1 or 0. 1 if i equal j, 0 if i is not j. Orthogonal eigenvectors. Now, what matrices have orthogonal eigenvectors?

We're going back to linear algebra because this is a fundamental fact to know, this family of wonderful matrices. Matrices with orthogonal eigenvectors. Or tell me one bunch of matrices that you know has orthogonal eigenvectors.

STUDENT: Symmetric.

GILBERT STRANG: Symmetric. And what is special about the eigenvalues? They're real. But there are other matrices that have orthogonal eigenvectors and we really should know the whole story about those guys. They're too important not to know. So, what's another bunch of matrices?

So, these symmetric matrices have orthogonal eigenvectors and-- real symmetrics and the eigenvalues will be real. Well, what other kind of matrices have orthogonal eigenvectors? But they might be complex and the eigenvalues might be complex.

And you can't know Fourier without saying, OK, I can deal with this complex number. OK, so what's another family of matrices that has orthogonal eigenvectors? Yes.

STUDENT: Diagonal matrices.

GILBERT STRANG: Diagonal for sure, right? And then we know that we have the eigenvectors go into the identity matrix, right. Yeah, so we know everything about diagonal ones. You could say those are included in symmetric. Now, let's get some new ones. What else?

STUDENT: [INAUDIBLE]

GILBERT STRANG: Orthogonal matrices count. Orthogonal matrices, like permutations or like rotations or like reflections. Orthogonal matrices. And what's special about their eigenvalues? The eigenvalues of an orthogonal matrix?

STUDENT: [INAUDIBLE]

GILBERT STRANG: The magnitude is 1, exactly. It has to be 1 because an orthogonal matrix doesn't change the length of the vector. Q times x has the same length as x for all vectors. And in particular, for eigenvectors.

So, if this was an eigenvector, Q x would equal lambda x. And now if that equals that, then lambda has to be 1. The magnitude of lambda has to be 1. Of course.

Complex numbers are expected here and that's exactly what we're seeing here. All the eigenvalues of permutations are very special orthogonal matrices. I won't add permutations separately to the list but they count.

The fact that this is on the list tells us that the eigenvectors that we're going to find are orthogonal. We don't have to do a separate check to see that they are once we compute them. They have to be. They're the eigenvectors of an orthogonal matrix.

Now, I could ask you-- let's keep going with this and get the whole list here. Along with symmetric there is another bunch of guys. Antisymmetric. Big deal, but those are important.

So, symmetric means A transpose equals A. Diagonal you know. A transpose equals A inverse for orthogonal matrices.

Now, I'm going to put in antisymmetric matrices where A transpose is minus A. What do you think you know about the eigenvalues for antisymmetric matrices? Shall we take a example? Anti symmetric matrix.

Say 0, 0, 1, and minus 1. What are the eigenvalues of that? Well, if I subtract lambda from the diagonal and take the determinant, I get lambda squared plus 1 equals 0. So lambda is i or minus i.

That's a rotation matrix. It's a rotation through 90 degrees. So there could not be a real eigenvalue. Have you thought about that? Or a real eigenvector. If I rotate every vector, how could a vector come out a multiple of itself? How could I have A transpose times the vector equal lambda times a vector?

I've rotated it and yet it's in the same direction. Well, somehow that's possible in imaginary space and not possible in real space. OK, so here the lambdas are imaginary. And now finally, tell me if you know the name of the whole family of matrices that includes all of those and more. Of matrices with orthogonal eigenvectors.

So, what are the special properties then? These would be matrices. Shall I call them M for matrix? So, it has orthogonal eigenvectors. So it's Q times the diagonal times Q transpose.

I've really written down somehow-- I haven't written a name down for them but that's the way to get them. I'm allowing any orthogonal eigenvectors. So, this is diagonalized. I've diagonalized the matrix.

And here are any eigenvalues. So, the final guy on this list allows any eigenvalues, any complex numbers. But the eigenvectors, I want to be orthogonal. So that's why I have the Q.

So, how would you recognize such a matrix and what is the name for them? We're going beyond 18.06, because probably I don't mention the name for these matrices in 18.06, but I could. Anybody know it? A matrix of that form is a normal matrix. Normal.

So, that's the total list, is a normal matrix. So, normal matrices look like that. I have to apologize for whoever thought up that name, normal. I mean that's like, OK. A little more thought, you could have come up with something more meaningful than just, say, normal.

[INAUDIBLE] that's the absolute opposite of normal. Almost all matrices are not normal. So anyway, but that's what they're called. Normal matrices.

And finally, how do you recognize a normal matrix? Everybody knows how to recognize a symmetric matrix or a diagonal matrix, and we even know how to recognize an orthogonal matrix or skew or antisymmetric. But what's the quick test for a normal matrix? Well, I'll just tell you that a normal matrix has M transpose M equal M M transpose.

I'm talking here about real matrices and I really should move to complex. But let me just think of them as real. Well, the trouble is that the matrices might be real but the eigenvectors are not going to be real and the eigenvalues are not going to be real. So, really I-- I'm sorry to say really again-- I should get out of the limitation to real. Yeah.

And how do I get out of the limitation to real? What do I change here if M is a complex matrix instead of a real matrix? Then whenever you transpose it you should take its complex conjugate. So now that that's the real thing. That's the normal thing, that's the right thing. Yeah, right thing. Better.

OK, so that's a normal matrix. And you can check that if you took that M and you figured out M transpose and did that, it would work. Because in the end the Q's cancel and you just have 2 diagonal matrices there and that's sort of automatic, that diagonal matrices commute. So, a normal matrix is one that commutes with its transpose. Commutes with its transpose or its conjugate transpose in the complex case.

OK, why did I say all that? Simply because-- oh, I guess that-- so the permutation P is orthogonal so its eigenvectors, which we're going to write down in a minute, are orthogonal. But actually, this matrix C will be a normal matrix. I didn't see that coming as I started talking about these guys.

Yeah, so that's a normal matrix. Because circulant matrices commute. Any 2 circulant matrices commute. C1 C2 equals C2 C1. And now if C2 is the transpose of-- so, here's a matrix. Yeah, so these are matrices here.

Circulants all commute. It's a little family of matrices. When you multiply them together you get more of them. You're just staying in that little circulant world with n parameters.

And once you know the first row, you know all the other rows. So in fact, they all have the same eigenvectors. So, now let me be sure we get the eigenvectors straight. OK.

OK, eigenvectors of P will also be eigenvectors of C because it's a combination of powers of P. So once I find the eigenvectors of P, I've found the eigenvectors of any circulant matrix. And these eigenvectors are very special, and that's the connection to Fourier.

That's why-- we expect a connection to Fourier because we have something periodic. And that's what Fourier is entirely about. OK, so what are these eigenvectors? Let's take P to be 4 by 4.

OK, so the eigenvectors are-- so we remember, the eigenvalues are lambda equal 1, lambda equal minus 1, lambda equal I, and lambda equal minus I. We've got 4 eigenvectors to find and when we find those, you'll have the picture. OK, what's the eigenvector for lambda equal 1?

STUDENT: 1, 1, 1, 1.

GILBERT STRANG: 1, 1, 1, 1. So, let me make it into a vector. And the eigenvector for lambda equal minus 1 is? So, I want this shift to change every sign. So I better alternate those signs so that if I shift it, the 1 goes to the minus 1. Minus 1 goes to the 1. So the eigenvalue is minus 1.

Now, what about the eigenvalues of i? Sorry, the eigenvector that goes with eigenvalue i? If I start it with 1 and I do the permutation, I think I just want i, i squared, i cubed there. And I think with this guy, with minus i, I think I want the vector 1, minus i, minus i squared, minus i cubed.

So without stopping to check, let's just see the nice point here. All the components of eigenvectors are in this picture. Here we've got 8 eigenvectors. 8 eigenvalues, 8 eigenvectors.

The eigenvectors have 8 components and every component is one of these 8 numbers. The whole thing is constructed from the same 8 numbers. The eigenvalues and the eigenvectors. And really the key point is, what is the matrix of eigenvectors?

So, let's just write that down. So, the eigenvector matrix for all circulants of size N. They all have the same eigenvectors, including P. All circulants C of size N including P of size N.

So, what's the eigenvector matrix? What are the eigenvectors? Well, the first vector is all 1's. Just as there.

So, that's an eigenvector of P, right? Because if I multiply by P, I do a shift, a cyclic shift, and I've got all 1's. The next eigenvector is powers of w.

And let me remind you, everything is going to be powers of w. e to the 2 pi i over N. It's that complex number that's 1/n of the way around. So, what happens if I multiply that by P? It shift it and it multiplies by w or 1/w, which is another eigenvector.

OK, and then the next one in this list will be going with w squared. So it will be w fourth, w to the sixth, w to the eighth. Wait a minute, did I get these lined up all right? w goes with w squared. Whoops.

w squared. Now it's w to the fourth, w the sixth, w to the eighth, w to the 10th, w to the 12th, and w to the 14th. And they keep going. So that's the eigenvector with eigenvalue 1. This will have the eigenvalue-- it's either w or the conjugate, might be the conjugate, w bar.

And you see this matrix. So, what would be the last eigenvector? It would be w-- so this is 8 by 8. I'm going to call that the Fourier matrix of size 8. And it's the eigenvector matrix. So Fourier matrix equals eigenvector matrix.

So, what I'm saying is that the linear algebra for these circulants is fantastic. They all have the same eigenvector matrix. It happens to be the most important complex matrix in the world and its properties are golden. And it allows the fast Fourier transform, which we could write in matrix language next time.

And all the entries are powers of w. All the entries are on the unit circle at one of those 8 points. And the last guy would be w to the seventh, w to the 14th, w to the 21st, 28th, 35th, 42nd, and 49th. So, w to the 49th would be the last. 7 squared.

It starts out with w to the 0 times 0. You see that picture. w to the 49th. What is actually w to the 49th? If w is the eighth root of 1, so we have w to the eighth, it's 1 because I'm doing 8 by 8. What is w to the 49th power?

STUDENT: [INAUDIBLE]

GILBERT STRANG: w? It's the same as w. OK, because w to the 48th is 1, right? I take the sixth power of this and I get that w to the 48th is 1. So w to the 49th is the same as w.

Every column, every entry, in the matrix is a power of w. And in fact, that power is just the column number times the row number. Yeah, so those are the good matrices.

So, that is an orthogonal matrix. Well, almost. It has orthogonal columns but it doesn't have orthonormal columns. What's the length of that column vector?

STUDENT: [INAUDIBLE]

GILBERT STRANG: The square root of 8, right. I add up 1 squared 8 times and I take the square root, I get to the square root of 8. So, this is really-- it's the square root of 8 times an orthogonal matrix.

Of course. The square root of 8 is just a number to divide out to make the columns orthonormal instead of just orthogonal. But how do I know that those are orthogonal?

Well, I know they have to be but I'd like to see it clearly. Why is that vector orthogonal to that vector? First of all, they have to be. Because the matrix is a normal matrix. Normal matrices have orthogonal-- oh yeah, how do I know it's a normal matrix?

So, I guess I can do the test. If I have the permutation P, I know that P transpose P equals P P transpose. The permutations commute.

So, it's a normal matrix. But I'd like to see directly why is the dot product of the first or the 0-th eigenvector and the eigenvector equals 0? Let me take that dot product. 1 times 1 is 1. 1 times w is w. 1 times w squared is w squared. Up to w to the seventh, I guess I'm going to finish at, equals 0.

Well, what's that saying? Those numbers are these points in my picture, those 8 points. So, those are the 8 numbers that go into that column of-- that eigenvector. Why do they add to 0? How do you see that the sum of those 8 numbers is 0?

STUDENT: There's symmetry.

GILBERT STRANG: Yeah, the symmetry would do it. When I add that guy to that guy, w to the 0, or w to the eighth, or w to the 0. Yeah, when I add 1 and minus 1, I get 0. When I add these guys I get 0. When I add these-- by pairs. But what about a 3 by 3?

So, 3 by 3. This would be e to the 2 pi i over 3. And then this would be w to the 4 pi-- this would be w squared, e to the 4 pi i over 3. And I believe that those 3 vectors add to 0.

And therefore they are orthogonal to the 1, 1, 1 eigenvector because the dot product will just want to add those 3 numbers. So why is that true? 1 plus e the 2 pi i over 3 plus e to the 4 pi over 3 equals 0.

Last minute of class today, we can figure out how to do that. Well, I could get a formula for-- that sum is 1 and I could get a closed form and check that I get the answer 0. The quick way to see it is maybe suppose I multiply by e to the 2 pi i over 3.

So, I multiply every term, so that's e to the 2 pi i over 3. e to the 4 pi i over 3. And e to the 6 pi i over 3. OK, what do I learn from this?

STUDENT: [INAUDIBLE]

GILBERT STRANG: It's the same because e to the 6 pi i over 3 is?

STUDENT: 1.

GILBERT STRANG: Is 1. That's 2 pi i, so that's 1. So I got the same sum, 1 plus this plus this. This plus this plus 1.

So I got the same sum when I multiplied by that number. And that sum has to be 0. I can't get the same sum-- I can't multiply by this and get the same answer unless I'm multiplying 0. So that shows me that when n is odd I also have those n numbers adding to 0.

OK, those are the basic-- the beautiful picture of the eigenvalues, the eigenvectors being orthogonal. And then the actual details here of what those eigenvectors are. OK, good. Hope you have a good weekend, and we've just got a week and a half left of class.

I may probably have one more thing to do about Fourier and then we'll come back to other topics. But ask any questions, topics that you'd like to see included here. We're closing out 18.065 while you guys do the projects. OK, thank you.

Problems for Lecture 31
From textbook Section IV.2

3. If \(\boldsymbol{c\ast d} = \boldsymbol{e}\), why is \((\sum c_i)(\sum d_i)=(\sum e_i)\)? Why was our check successful?
\((1+2+3)\,(5+0+4)=(\boldsymbol{6})\,(\boldsymbol{9})=\boldsymbol{54}=5+10+19+8+12\).

5. What are the eigenvalues of the 4 by 4 circulant \(C=I+P+P^2+P^3\)? Connect those eigenvalues to the discrete transform \(F\boldsymbol{c}\) for \(\boldsymbol{c}=(1,1,1,1)\). For which three real or complex numbers \(z\) is \(1+z+z^2+z^3=0\)?

Free Downloads

Video

• Internet Archive (MP4 - 117MB)

Caption

• English-US (SRT)