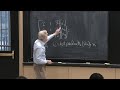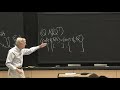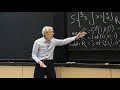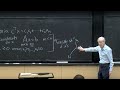Lecture 14: Low Rank Changes in A and Its Inverse

• Download English-US transcript (PDF)

The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high-quality educational resources for free. To make a donation or to view additional materials from hundreds of MIT courses, visit MIT OpenCourseWare at ocw.mit.edu.

GILBERT STRANG: So just to orient where we are, today starts a new chapter about low-rank matrices. So that's an important bunch of matrices. They can be truly low-rank, like uv transpose. That's a rank 1. And we have some questions about those. And then later in the chapter, we'll meet matrices that are approximately low-rank, where the singular values drop off like crazy. And those are quite remarkable matrices.

So this is my topic at the beginning-- and if it doesn't take the whole hour, I want to go back to a topic in chapter 2-- that should be 2.4-- where we were last time. Good. So that's for later in the hour. This is for now.

Let's focus on this. So what's the question there? I start with the identity matrix. I perturb it by a matrix of rank 1. And I ask what the inverse is. So I'm making a small change in the matrix.

When I say small change, I don't mean that the numbers are small. In fact, uv transpose could be the all 1's matrix, or the all millions matrix, even. But its rank is small. That's the idea of small that's important here.

And I would like to know what the inverse is. So that's the question here in 4.1. And there's a famous formula that has at least three names, and probably more, and it's also called the matrix inversion formula in signal processing. And let me write down the example.

So I start with the identity matrix. I do a rank 1 perturbation. And I want to know, what's the inverse? And I'll write down the answer and check that it's correct.

So I'm perturbing the identity matrix in this case, whose inverse is also the identity matrix. So I'm going to write the answer as a perturbation of I. And the question is, what is that perturbation? And it's a famous formula. There is a uv transpose that comes in, copied from there, divided by 1 minus v transpose u.

Now, let's first of all just see that this is a reasonable formula. So u a column-- u and v are column vectors, as always. So uv transpose is a matrix, column times row. And it's being subtracted from the identity.

And over here on this side, I have uv transpose-- again, a rank 1 matrix-- divided by a number. So that's the point. This is a number-- a 1 by 1 matrix, you could say.

So the point of this formula is to find the inverse of an n by n matrix in terms of the inverse of a 1 by 1 matrix, which is a lot simpler and easier to do. I mean, that right-hand side is clearly easy. And let's see what other things it tells us.

So this was a rank 1 perturbation in the identity. Then when I invert, I get-- look at this. This is also a rank 1. That's a number. In fact, it's the very same rank 1 that we had there in this nice case.

So conclusion-- if I change a matrix by rank 1, I change its inverse by rank 1. That doesn't seem completely obvious until you go to figure it out. When you figure it out, you get a formula that tells you.

Well, so far what I'm perturbing is the identity matrix. When I get here, I'm going to perturb any matrix. And I'm going to reach the same conclusion. If this is rank 1, then the change in the inverse is also rank 1. But let's see it first for a equal to the identity.

So I guess I have two or three questions. One would be, how do you check that this is correct? Again, remember what it's doing. It's pretty neat. It's computing an n by n inverse in terms of a 1 by 1 inverse. It's a number.

And that's certainly a favorable exchange. So it's a formula that you want and a formula that's quite useful. Let me just check the formula before I talk about how it's useful.

So how shall I check it? I guess, if this is claimed to be the inverse, then let's just che-- so this will be the check. I'll multiply by that, I plus uv transpose over 1 minus v transpose u, the claimed inverse. And what am I hoping to get from this multiplication?

AUDIENCE: I.

GILBERT STRANG: I. I'm hoping that, that result is the identity matrix. So I'm just going to do it out, and we'll see the identity appear.

So that times I-- so let me just write that part first, I minus uv transpose. And now I minus uv transpose times this-- so that's I minus uv transpose times uv transpose over 1 minus v transpose u. It's just multiplying it out and seeing that we get the identity.

I see the identity there. So I guess, I hope that all this part reduces to-- what does it reduce to? Let me do that numerator there. So that's uv transpose minus u-- ooh-- minus u times v transpose u-- do you see what's happening here-- v transpose.

The key is that when I multiplied that times that, I've got four things in a row. And I do the middle pair first. Because that's a number, v transpose u. So I had uv transpose from that and uv transpose times that number minus-- do you see-- what have I got here? I've got--

AUDIENCE: [INAUDIBLE]

GILBERT STRANG: Yeah. I've got uv transpose. Now I factor out a 1 minus v transpose u, which is just what I want. I factor the 1 minus v transpose u out of here. It's there. Cancel those. And then I'm left with a uv transpose, which cancels that and leaves the identity.

It's kind of magic. Of course, somebody had to figure out that formula in the first place. I could do the next one, if you like, since I'm on a roll. Suppose I take this second one, now what's the difference in-- it's uv transpose, but those are larger letters, the u and the v. So what am I meaning by those?

Those are matrices. This is a bigger rank. u has k columns. v transpose has k rows. That product uv transpose is k by k. So let me see what I think the formula would be.

So now, I minus uv transpose inverse-- so this is n by k times k by n. So it's n by n matrix. And this is the ide-- identity of this. But its rank is-- what is the rank of that now?

AUDIENCE: k.

GILBERT STRANG: k. Right. So I have here, the whole thing is the inverse of an n by n matrix. So I have an n by n matrix. Let me put that up here, n by n matrix to invert.

There it is. I'm going to write down the formula. And you're going to be able to write it down, because it's just copied from that one. And you'll see that it involves a k by k inverse.

So I have an n by n matrix to invert, but I don't have to do that. I can switch it to a k by k matrix. That's pretty nice. So let's do it.

So I'm basically gonna copy that I plus u-- now, I've matrices. So that's an inverse, but I can't leave it as a denominator. Because through here, we're talking about a k by k matrix.

So I have to put it like any matrix inverse, Ik minus v transpose u inverse. So I'm just copying this formula, wisely taking the u first, then this part, then finally, the v transpose. I put this one up. This one now has made that one obsolete. This was the case k equal to 1 over here.

But I think it helps to see it. It certainly helps me to see the formula first for a rank 1 perturbation, which is a very likely possibility, and then see that we have a totally analogous formula. It's sort of fun to check it. So I plan to do the same check. But I'll just notice here that I have a k by k inverse.

So I'm exchanging something that's a perturbation of n by n identity, an n by n matrix, to have to invert something that's a k by k matrix, perturbing the k by k identity, much smaller. In that case, k was 1. So are you good for checking it now? So I want to multiply that by this and hopefully get In, the identity. This is the n by n identity.

I haven't given credit to the two or three or four, or possibly 11 people, who found this formula. And I'm not see-- oh, yeah, here are their names. Is it OK to make them famous by putting their names up here?

Yes. Sherman-- and I couldn't tell you who did what. Morrison, Woodbury, and then no doubt others-- maybe one of them did this rank 1 case, and then another generalized it. And then you could see from the outline there that eventually we'll-- we can perturb a matrix A. Of course, that's not going to be much harder than the identity.

Let's do just one more check, and then show how it could be used. I multiply that by that. Can we do that-- this thing times this, and hope to get the identity? So first, I'll write down this thing. So I won't put equal, because I'm multiplying that by that.

So I get In minus uv transpose. On the left side, of course, I'm getting the identity, and hoping I'm getting the identity on the right. So I'm multiplying by this. I did it there.

Now I have to put I minus uv transposed. It takes faith here. u I minus v transpose u inverse v transpose-- gulp. Shall I just leave it there? Or you're-- had lunch, you're strong. Let's see what we can do.

This part-- fine. This part-- oh, boy. What do I do here?

That trick is going to be that this dopey-looking thing there can be written differently. Well, just tell me what it equals. It equals u minus uv transpose u. Everybody sees that. But now what am I going to do?

I'm going to put the parentheses differently. I'm bringing u, the u that was on the right up there-- I'm going to put it on the left. You see that?

So this is obviously u minus uv transpose u. And now I'm going to write it another time. It's u times I minus v transpose u. I'm going to factor the u out on the left side instead of where it originally came on the right side of this.

You see the great news there? This was actually well-organized by your professor-- by accident. So what do I do now? This thing-- look. I've got exactly here what I've got inverted there.

So altogether, I have I minus uv transpose plus this u, this cancelled, times v transpose. So I get I. So it was just this little sleight of hand, where u came in on the right and came out on the left side. And there'd be a similar formula with A in there.

So now, it's a fair question, how did anybody come up with these formulas? We're proving them correct just by checking that they give the identity matrix. We should really think how to find the formula in the first place. I could go back to this one. How could you find that formula in the first place?

Well, here is one way to do it. This is then about "to discover the formula." And then, over here, let me put over here "to use the formula," while I think of it.

And actually, I have two uses in mind. Use one would be to solve-- I'm just doing I. Suppose I want to-- so this is my new matrix uv transpose x equals some right-hand side b. Solve a linear system that has that coefficient matrix.

The use two would be, in least squares, a new measurement or observation or data point in these squares. So what do I mean by this? The old problem was Ax equal b.

And I'm thinking, when I'm talking about least squares here, I'm imagining that A is rectangular. Too many equations-- A is a tall, thin matrix, just the kind we've been talking about. So that equation becomes-- of course, we know we go to the normal equations-- A transpose Ax, the good x, is A transpose b.

Now we get a new measurement. So a new measurement, how does a new measurement change the problem? So this is the old problem before the measurement comes in. Now a new measurement arrives. So that's another b, a b M plus 1.

And we get another equation. We get another equation. That's the new measurement, new point to get this straight line it's trying to stay close to. So we'll call this equation-- I don't know what we should call it. Maybe it'll be one more row.

So now, old now is becoming new. I'm sort of more excited about this than proving the formula. So I'll just keep going.

So there is our M measurements, M being large, A being a tall, thin matrix. And now we're going to give it one more row. We're going to make it even taller, say maybe, v transpose times this same x is some b new, or something like that. So there's one more row, one more measurement. So what happens to the normal equation?

This makes it even more likely. There's another point, hoping that a straight line will go through. But if we give it one more point, there is even less chance of a straight line going exactly through. But still, so what do I-- this is my new matrix. So what's my new normal equation?

The new normal equation, the A, or transpose-- the A has got a new row. A has got a new row. So a transpose will have a new column. I'm just copying the normal equation, but I'm giving it its new thing. It's got a new column.

That is my A with a new row. This is my x hat, my least squares answer, new. And A transpose is this. A transpose with a new, now, column times b, so b and b new.

Pretty OK with this. Do you see that this is the new normal equation? I'm using the new matrix and the new right-hand side. And just one more data point has come into the system from the sensor. And what's the key point here?

The key point is I don't want to recompute. I don't want to multiply that matrix again. I don't want to start over. I don't want to compute this A transpose times that A. I want to use what I've already done.

If I multiply those two together, what do I actually get? So this is, I'm adding a new column here and a new row here. Tell me what you think the answer is, and then let's just see why. I'm asking you what that matrix is. What do you think?

Start me out, anyway. I'm just asking for ordinary matrix multiplication. Well, I guess I'm asking you to do it columns times rows since that's what 18 and 6.5 specializes in.

So I think I have that times that, A transpose A, plus one new column times one new row. vv transpose is multiplying this x hat new. And over on the right side, I get whatever I had, the A transpose b old and the v b new.

But let me come back to that, because that really shows you why you must understand matrix multiplication, both the usual row times column-- but that would not be so attractive here-- and also the new way as columns times rows. Because when I see it as columns times rows, I see that I have the same columns and same rows there. So that's just what I already knew.

And then I have one new column times one new row. Of course, that's column n plus 1, and that's a row n plus 1. And they give that rank 1. It's a rank 1 change in A transpose A. It's a rank 1 change in A transpose A.

So this is like part of least squares. I mean, you can see the relevance in a real problem. You maybe have a missile flying along. You've sent up a satellite, GPS satellite. You're tracking it. More data comes in. The data is just one more position.

The tracker isn't perfect. So we're going to fit-- well, here I'm fitting a straight line, maybe. But we're fitting to the data. And the only change in the left-hand, the big problem, the big part of the computation is the A transpose A part. And it's just changed by rank 1, or by rank k, if we had k new data points. If we had k new data points, then this would be a rank k matrix.

So you see, then I go back here-- well, OK. Now I'm perturbing A transpose A. And I haven't given a formula for that one yet. I've only perturbed up to, now, the identity. But you can believe, since all these formulas are working, that Sherman or Morrison or Woodbury came up with the correct perturbation for A transpose A.

So I'm sort of happy that, that application, so natural, came out so simply. While I'm on that sort of subject, have you ever heard of the Kalman filter? So that Kalman filter, what's that about?

It's about exactly this. It's about dynamic least squares. It's about least squares problems in which new data is coming in. That's what the Kalman filter-- or in other words, let me just write a couple of words up here.

This is really recursive least squares. Recursive least squares-- what I mean by recursive is new data comes in. It changes the answer, but it doesn't change our method.

And then the Kalman filter is a very, very big deal in guidance. If you're sending up a missile, a satellite, you track it. You do just what I've been discussing here.

But the Kalman filter is-- it's got more possibilities built in than this one. This is the simplest update possible. And it would go in this category. Kalman went beyond a standard update. How did he go beyond?

Let's see. If I've used the words Kalman filter, I should tell you what it is that Kalman does and what is that least squares problem. It's just part of general knowledge, it seems to me. So what is it, more gen-- what are the additional pieces?

You've seen the main idea here of getting a simple recursive step that doesn't require recomputing all that you did before. And of course, to this inverse, I'm going to apply the Sherman-Morrison-Woodbury formula. So I'll use the inverse that I had before. And this will be a rank 1-- this is a rank 1 perturbation of that.

I'm looking here at A transpose A. Over there, I was looking at, I just called it A. Or I even called it the identity matrix. But it's whatever matrix you have here with a rank 1 perturbation. And the whole thing has to be inverted.

And so I was going to say what is additional, just so you know about Kalman filters. So two things are additional. The point is Kalman filters are for dynamic least squares. I would say dynamic squares. And so there are two ingredients that you haven't seen here.

One ingredient is the idea of using the covariance matrix, which tells you how errors are correlated. So that would be weighted least squares, or correlated least squares. So these squares-- let me just remind you, if I can write it here.

So least squares-- standard. Standard meaning that data is not correlated. It all has the same variance. These are the statistics words that I'm using last time and this, but that I'll talk about properly.

So the standard one is the covari-- the standard means covariance equal the identity matrix. You're doing Gaussian normal probability but with just standard Gaussians, standard Gaussians. So that's one aspect, which in the work of the Draper lab, let's say, they have to think, OK, they're getting sensors, different kinds of sensors, with different accuracies, different reliability. So they have to take account of the covariance matrix.

Then the other point is-- and also-- so that was point one. Point two is the dynamic part. There is a state equation. So I'm really into the edge of control theory.

So let me just use some words here that you've seen, if you've-- so control theory has state equation. What's a state equation? What is the state? This is the position, in my example, is the position of the satellite.

So are we looking for a fixed satellite? Certainly not. The satellite is moving. So this state equation tells me how much the satellite-- it's Newton's law-- tells me where the satellite should be. Where am I looking?

And then the least squares tells me, it says, look around that sort of median position for the actual position that the data is giving. So just to say-- let me-- let me summarize this. The Kalman filter is a significantly improved version of recursive least squares. That's recursive least squares.

New measurement comes in, changes things but leaves a big part unchanged. And you find that new x hat. With a Kalman filter, there's an covariance matrix in the middle here. That's where covariance matrices go. That's matrix covariance, or inverse covariance, times that.

And oh, why don't we see the covariances at the right time? So maybe those minutes that I've occupied were just really to get you to hear that name for the simplest update. And Kalman's name for a more general update. Done.

Oh, this is also to be done. Where is-- yeah. No-- up at the top. I seem to be into the applications here. I promised how to discover the formula. Maybe I'll never know. Because I'm really more interested in, what's it good for?

Use number one, now, I'm backing up to the easy, easy question. Suppose I had-- and let me even change the matrix to A here. It makes it more realistic. I'm going to copy that here, fully on discovering the formula. For the moment, let's just use it.

So I suppose that Au is b is solved for u. Now, now solve A plus-- or minus a rank-- let me do the rank 1, A minus uv transpose b. What's-- x. This is the problem that I really would like to solve. Let me just be sure I'm doing this right.

It's similar to what we had in the Kalman situation. Suppose I've solved one problem. But now I perturb the matrix by rank 1. So I have a new problem with a new answer. And I want to get that answer quickly. Yeah?

AUDIENCE: Are the u's related in those two lines?

GILBERT STRANG: Oh, no. Thank you. Thank you very much. Let's call this guy z, or w, maybe w. So thank you. That's great.

So that's what I've solved for w. In other words, I have found A inverse b. And I want to find the answer to that new question. So I've perturbed the matrix. It's the coefficient matrix in a linear system. And I just want to solve that linear system.

Now, so if I didn't know anything about the formulas, I would have a new matrix here. It would take n cube steps to do elimination and get the new answer. But the point is to use the old answer. The point is to use the old answer. And now let me just say what this is. And it's problem three in this section.

So in other words, we know about A. We've solved that one. So what I'm going to do, instead of solving a whole new problem, I'm going to-- so quickly is the idea.

And here's the idea. I've solved that one. And I'm going to solve a second problem, also solve, A with the same matrix A-- oops-- A times what shall I call the unknown? There's z equal u.

So this is my problem. I know the u and v transpose. But I don't really want to find the inverse of this matrix from scratch. So the idea is that if I suitably combine the solutions to the original problem, the original solution w, and the solution to this problem with the new guy u there, that somehow, by combining the w and the z, I'm going to get this answer x. That's where I'm headed. That's where I'm headed, that by figuring out w and z-- so do you see what I've done?

With the matrix A, I've solved two problems. Does that take twice as long? If I have the same matrix A but different right-hand sides, b and u, if I factor A into Lu, all the hard work is done there on the left side. All the work is done in finding Lu. And then I just back substitute to find the second solution.

This is so fundamental that I'm emphasizing it, that if you have multiple right-hand sides, you don't every time go back and work on the left side. The left side with the same matrix A, just would do the same stuff. The same rows and pivots and all that stuff will happen because it's the same A. You just attach-- you really just stick a second column-- really, the fast way to do it is A wz.

The two solutions come from the b and the u. I've just put the two problems together to emphasize that the matrix A is the same. This is where most of the work goes. But it only goes there once. That's the point.

Then finally, I'm supposed to-- the notes are supposed to tell me how to combine the two answers w and z to get the answer x. So let me write that down. And that will be use number one of the Sherman-Morrison-Woodbury formula. So I'm planning to just write it down.

According to this, step two is the answer we want, here written x-- so I haven't used the same letters as in the notes-- is the original w-- good-- and then a change. Because I've changed the problem. So I'm going to change the answer.

But the thing is, to get this answer, I have to divide by that determinant wherever it was, the-- oh, yeah, the-- I'm sorry. I'm using an A here, and I haven't given you the formula for A. So that'll have to wait. So I'll put determinant here. And Sherman, Morrison, Woodbury figured that out.

And then-- oh, I'm sorry. We know what that is. We want 1 minus v transpose z. So it's the v from here, 1 minus v transpose. And it's the z there. Oh, yeah. This is good.

So I'm going to get a formula that changes the solution w by a term that we recognize is coming from Sherman, Morrison, Woodbury. And that term in the numerator is a multiple of zx. So I'm using w-- yes-- w times-- sorry-- times x, which was-- I'm sorry. w is xv. So the v here, I'm just using-- the v is the same v. So v transpose z, I think that's got it. I think that's got it.

So again, the point was to-- x doesn't appear here, because that's what I'm after-- is to use the w and the z, the w and the z. And I have to use, of course, the v. And I have to use the u. And that got used here. So everything that had to be used got used. And that was the answer.

So that's the basic use, is, if I perturb the problem, the left-hand side, what's the change in the solution? Over here with least squares, it was the same. I perturbed the left-hand side. But because it was least squares, there was an A transpose A to deal with.

So this was one level more difficult, because it involved A transpose A's. And here, it was just straightforward A. So, yes? Thanks.

AUDIENCE: Would it be also a good idea-- so you have A minus uv transpose x plus b-- to write A minus Az b transpose x equals b? I'm backtracking on the left.

GILBERT STRANG: I could probably do this other ways. Yeah. Yeah. Yeah. I hope you follow up on that and write it down. So maybe what I've done is what my goal was for today, first, to show you the formula for the inverse; second, to recognize that it has interesting importance that a rank k change in the matrix brings a rank k change in the inverse, and that we can-- the formula says to invert an n by n matrix, you can switch an inverted k by k matrix. And then I spoke about a couple of the applications.

So the only thing I have not done is to give you the full Sherman-Morrison-Woodbury formula, the one with an A, the one that's up on the right. Can I do that finally? You can probably guess what it's going to be. Where is-- there's got to be one more blackboard.

So here Sherman-Morrison-Woodbury. And what's the complete thing? It's A minus uv transpose inverse. So this is n by n. And it's an A now instead of an identity matrix. That's the difference.

And this is n by k, k by n. So it's rank k perturbation. And start me out on the formula. What's the first thing I have to write?

AUDIENCE: A inverse.

GILBERT STRANG: A inverse. So I start with A inverse. And then I subtract something. And it's going to be a copy of this, except-- well, maybe it's just a perfect copy. Maybe I just need the u. I'm going from that left board. Now, Ik, what do I put it in there?

I am going to have to look. So we're writing down now the formula, the full scale-- OK. Oh, all right. Here it is.

There is an A inverse u. Now comes that whole thing inverted that you'll expect, I minus v transpose A inverse u, all inverse. And then there's another two pieces, v transpose A inverse.

So I didn't look ahead to get it at all on one line. But do you see what-- this is the-- oh, that's probably-- is that-- yeah. That's the identity. Because we've got enough A inverses.

I believe that's the final, ultimate formula of life here, that we've changed it by rank k. Here's the original inverse. And presumably, this is a rank k change. That will be a rank k change. And it only requires us to compute that inverse, where that's a k by k matrix.

Thank you for allowing this, our 50 minutes of formulas. So that's really what that comes to. So that's section 4.1 of the notes with some applications. And we will move on to other circumstances of low rank. Good. Thank you.

Problems for Lecture 14
From textbook Section III.1

1. Another approach to \((I-uv^{\mathtt{T}})^{-1}\) starts with the formula for a geometric series:
\((1-x)^{-1}=1+x+x^2+x^3+\cdots\)   Apply that formula when \(x = uv^{\mathtt{T}} =\) matrix:

\begin{eqnarray} \nonumber (I-uv^{\mathtt{T}})^{-1} &=& I+uv^{\mathtt{T}}+uv^{\mathtt{T}} uv^{\mathtt{T}}+uv^{\mathtt{T}} uv^{\mathtt{T}} uv^{\mathtt{T}}+\cdots \\ \nonumber &=& I+u\,[1+v^{\mathtt{T}} u+v^{\mathtt{T}} uv^{\mathtt{T}} u+\cdots]\,v^{\mathtt{T}} \end{eqnarray}

Take \(x=v^{\mathtt{T}} u\)  to see \(I+\dfrac{uv^{\mathtt{T}}}{1-v^{\mathtt{T}} u}\). This is exactly equation (1) for \((I-uv^{\mathtt{T}})^{-1}\).

4. Problem 3 found the inverse matrix \(M^{-1}=(A-uv^{\mathtt{T}})^{-1}\). In solving the equation \(My=b\), we compute only the solution \(y\) and not the whole inverse matrix \(M^{-1}\). You can find \(y\) in two easy steps:

\(\quad\) Step 1:   Solve \(Ax=b\) and \(Az=u\). Compute \(D=1-v^{\mathtt{T}} z\).

\(\quad\) Step 2:   Then \(y=x+\dfrac{v^{\mathtt{T}} x}{D}z\,\) is the solution to \(My=(A-uv^{\mathtt{T}})y=b\).

Verify \((A-uv^{\mathtt{T}})y=b\). We solved two equations using \(A\), no equations using \(M\).

Free Downloads

Video

• Internet Archive (MP4 - 112MB)

Caption

• English-US (SRT)