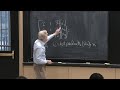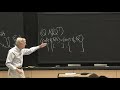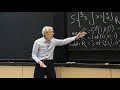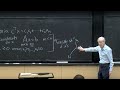Lecture 23: Accelerating Gradient Descent (Use Momentum)

• Download English-US transcript (PDF)

The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high quality educational resources for free. To make a donation, or to view additional materials from hundreds of MIT courses, visit MIT OpenCourseWare at ocw.mit.edu.

GILBERT STRANG: OK. So what I promised, and now I'm going to do it, to talk about gradient descent and its descendants. So from the basic gradient descent formula, which we all know-- let me just write that down-- the new point is the old point. We're going downwards, so with a minus sign that's the step size. And we compute the gradient at XK.

So we're descending in the direction of the negative gradient. And that's the basic formula, and is in every book studied. So my main reference for some of these lectures is the book by Stephen Boyd and Lieven Vandenberghe. And I mention again, Professor Boyd is talking, in this room, next week Wednesday, Thursday and he's speaking somewhere on Friday at 4:30-- and of course, about optimization.

And he's a good lecturer, yeah, very good. OK. So there's steepest descent, and I've redrawn my picture from last time. Now I'll go over there and look at that picture. But let me say what's coming. So that's pretty standard-- very standard, you could say. Then this is the improvement that is widely used. Adding in something called momentum to avoid the zigzag that we're going to see over there. And there's another way to do it. There's a Russian guy named Nesterov. His papers are not easy to read, but they've got serious content.

And one thing he did was find an alternative to momentum that also accelerated the descent. So this produces-- these both produce faster descent than the ordinary one. OK. And then you know, looking ahead, that for problems of machine learning, they're so large that the gradient-- we have so many variables-- all those weights are variables. And that could-- hundreds of thousands is not uncommon.

So then the gradient becomes a pretty big calculation, and we just don't have to do it all at once. We don't have to change-- so XK is a vector of all the weights, or-- and using-- and our equations are matching the training data. So we don't have to use all the training data at once, and we don't. We take a batch of training data, like one. But that's sort of inefficient in the opposite direction, to do them one at a time.

So we don't know want to do them one at a time, but we don't want to do all million at a time. So the compromise is a mini batch. So stochastic gradient descent does a mini batch at a time-- a mini batch of training, of samples training data each step. And it can choose them stochastically-- meaning randomly, or more systematically-- but we do a batch at a time. And that will come after the-- it'll come next week after a marathon, of course, on Monday. OK.

So let me just go back to that picture for a moment, but then the real content of today is this one with momentum added. OK. I just-- I probably haven't got the picture perfect yet. I'm just not an artist, but I think I'm closer. So this is-- those are the level sets. Those are the sets f of x equal constant. And in our model problem, f of x is x1 squared-- or let's say x squared plus b-y squared equal constant with small b-- b below 1 and maybe far below 1. So those are ellipses.

Those are the equations of an ellipse, and that's what I tried to draw. And if b is small, then the ellipses are long and thin like that. And now, what's the picture? You start with a point x nought, and you descend in the steepest direction. So the steepest direction is perpendicular to the level set, right? Perpendicular to the ellipse. So you're down, down, down. You're passing through more ellipses, more ellipses, more ellipses.

Eventually, your tangent to a-- it seems to me it has to be tangent. I didn't read this, but looks reasonable to me that the farthest in level set-- farthest in ellipse-- you're tangent to, and then you start going up again. So that's the optimal point to stop to end that step. And then where does the next step go? Well, you're here. You're on an ellipse. That's a level set.

You want to move in the gradient direction. That's perpendicular to the level set. So you're going down somewhere here, and you're passing again through more and more ellipses, until you're tangent to a smaller ellipse here. And you see the zigzag pattern. And that zigzag pattern is what we see, by formula, in Boyd's book, and many other places, too. The formula has those powers of the magic number. So we start at the-- start at the point b1, and follow this path.

Then the X's are the same b times this quantity to the kth power. And here is that quantity, b minus 1 over b plus 1. So you see, for a small b, that's a negative number. So it's flipping sine in the X's, as we saw in the picture. At least that part of the picture is correct. The y's don't flip sine. So this was XK, and when k is 0, we got b. YK is, I think, is not flipping sine. So that looks good.

And then FK-- the value of f-- also was the same quantity. FK is that same quantity to the kth times f0. So that quantity's all important. And so the purpose of today's lecture, is to tell you what the momentum term-- what improvement-- what change that brings in the basic steepest descent formula. I'm going to add on another term, which is going to have some-- give us some memory of the previous step. And so when I do that, I want to track that kind of descent for the new-- for the accelerated descent, and track it and see what improvement the momentum term brings.

And so the final result will be to tell you the improvement in the-- produced by the momentum term. Maybe while I have your attention, I'll tell you what it is now. And then will come the details, the algebra. And to me-- so this is as my own thought-- it's a miracle that the algebra, which is straightforward-- you really see the value of eigenvectors. We explained eigenvectors in class, but here you see why-- how to use them. That is really a good exercise.

But to me it's a miracle that the expression with momentum is very much like that expression, but different, of course. The decay-- the term that tells you how fast the decay is-- is smaller. So you're taking kth power. So let me-- I'll write that down, if that's all right. I didn't plan to do-- to reveal the final result at the beginning of the lecture. But I think you want to see where we're going. So with momentum-- and we have to see what that means-- this term of 1 minus b over 1 plus b becomes-- changes to-- 1 minus square root of b over 1 plus square root of b.

So I mentioned that before, but I don't think I wrote it down as clearly. So the miracle to me is to get such a nice expression for the-- because you'll see the algebra is-- it works, but it involves more terms because of momentum, involves doing a minimization of eigenvalues, and yet it comes out nicely. And then you have to see the importance of that. So let me-- I will just take the same example that I mentioned before. If b is 1 over 100, then this is 0.99 over 1.01. I think that these-- there's a square here, 2k.

So if we're-- so I'll just keep the square there, no big change, but I'm looking at-- now here-- at the square. Maybe squares are everywhere. OK. So that's close to 1. And now let's compare that with what we have. So if b is 1 over 100-- so I'm taking b to be 1 over 100-- and square root of b is 1 over 10. So this is 0.9 over 1.1 squared. And there's a tremendous-- that's a lot smaller than that is. Right. 9/10-- 9 over 11, compared to 99 over 101.

This one is definitely-- oh, sorry. Yeah, this reduction factor is well below that one. So it's a good thing. It's worth doing. And now what does it involve? So I'll write down the expression for the stochastic-- here we go. OK. So here's one way to see it. The new X is the old X minus the gradient. And now comes an extra term, which gives us a little memory. Well, sorry.

The algebra is slightly nicer if I write it a little bit differently. I'll create a new quantity, ZK, with a step size. OK. So if I took ZK to be just the gradient, that would be steepest descent. Nothing has changed. But instead, I'm going to take ZK-- well, it's leading term will be the gradient. But here comes the momentum term. I add on a multiple beta. One way to do it is of the previous Z. So the Z is the search direction. Z is the gradient you're traveling. It is the direction you're moving.

So it's different from that direction there. That direction was the gradient. This direction is the gradient corrected by a memory term, a momentum term. And one way to interpret that is to say that that ball-- is to think of a heavy ball, instead of just a point. I think of a heavy ball. It, instead of bouncing back and forth as uselessly as this one, it tends to-- it still bounces, of course, on the sides of the level set-- but it comes down the valley faster.

And that's the effect of this. So you could play with different adjustment terms, different corrections. So I'll follow through this one. Nesterov had another way to make a change in the formula, and there are certainly others beyond that. OK, so how do we analyze that one? Well, the real point is, we've sort of, by taking-- by involving the previous step, we now have a three level method instead of a two level method, you could say.

This involves only level K plus 1 and level K. The formulas now involve K plus 1K, and K minus 1. It's just like going from a first order differential equation to a second order differential equation. I'm not really thinking that K is a time variable. But in the analogy, K could be a time variable. So that here we had a first order equation. If I wanted to model that, it's sort of a DXDT coming in there, equal gradient. And these models are highly useful and developed for sort of a continuous model of steepest descent-- a continuous motion instead of the discrete motion. OK.

So that would-- that continuous model for that guy would be a first order in time. For this one, it'll be second order in time. And second order equations, of course, and there'd be constant coefficients in our model problem. And the thing about a second order equation that we all know is, there is a momentum term-- a damping term, you could say-- in multiplying the first derivative. So that's what a second order equation offers-- is the inclusion of a damping term which isn't present in the original first order. OK.

So how do we analyze this? I have to-- so how do you analyze second order differential equations? You write them as a system of two first order equations. So that's exactly what we're going to do here, in the discrete case. We're going to see-- because we have two equations. And they're first order, and we can-- let me play with them for a moment to make them good. OK. So I'm going to have-- so this will go to two first order equations, in which the first one-- I'm just going to copy, XK plus 1 is XK minus that step size ZK.

Yeah. OK. Yeah. OK. Time the previous times step here-- the next time step on the left. OK. So I just copied that. Now this one I'm going to increase K by 1. So in order to have that looking to match this, I'll write that as ZK plus 1, and I'll bring the K, saying, grad FK plus 1 equal beta ZK. That work with you? I just, in this thing, instead of looking at it at K, I went to K plus 1. And I put the K plus 1 terms on one side. OK.

So now I have a-- let's see. Let's remember, we're doing-- the model we're doing is F equal a half X transpose SX. So the gradient of F is SX. So what I've written there, for gradient, is really-- I know what that gradient is. So that's really SX K plus 1. OK. How to analyze that. What happens as K travels forward 1, 2, 3, 4, 5? We have a constant coefficient problem at every step. The XZ variable is getting multiplied by a matrix.

So here's XZ at K plus 1. And over here will be XZ at step K. And I just have to figure out what matrix is multiplying here and here. OK. And I guess here I see it. For the first equation has a 1 and a minus S, looks like, in the first row. And it has a beta in the second row. And here the first equation has a 1, 0 in that row. And then a minus S. So I'll put in minus S, multiplying XK plus 1, and then the 1 that multiplies ZK plus 1. Is that all right?

Sorry. I've got two S's, and I didn't draw that one-- didn't write that one in large enough, and I'd planned to erase it anyway. This is the step sizes. This is the matrix. But it's not quite fitting its place. This is the point where I'm going to use eigenvalues. I'm going to follow each eigenvalue. That's the whole point. When I follow each eigenvalue-- each eigenvector, I should say-- I'll follow each eigenvector of S. So let's do that.

So eigenvectors of S-- what are we going to call those? Lambda, probably. So SX equal lambda X. I think that's what's coming. Or Q. To do things right, I want to remember that S is a positive, definite symmetric matrix. That's why I call it S, instead of A. So I really should call the eigen-- it doesn't matter, but to be on the ball, let me call the eigenvector Q, and the eigenvalue lambda. OK.

So now I want to follow this eigenvector. So I'm supposing that XK is sum CK times Q. I'm assuming that X is in the-- tracking this eigenvector. And I'm going to assume that ZK is some other constant times Q. Everybody, do you see? That's a vector and that's a vector. And I want scalars. I want to attract just scalar CK and DK. So that's really what I have here. This was a little tricky, because X here is a vector, and two components are N components.

I didn't want that. I really wanted just to track an eigenvector. Once I've settled on the direction Q, everything is-- all vectors are in the direction of Q. So we just have numbers C and D to track. OK. So I'm going to rewrite this correctly, as, yeah. Well, let me keep going with this little formula. Then what will-- I needed an SX. What will SXK be? If XK is in the direction of the eigenvector Q, and it's CK-- what happens when I multiply by S?

Q was an eigenvector. So the multiplying by S gives me a--

AUDIENCE: Eigenvalue.

GILBERT STRANG: Eigenvalue, right? So it's CK lambda Q. Everything is a multiple of Q. And it's only those multiples I'm looking for, the C's and the D's. And then the lambda comes into the S term. Yeah. I think that's probably all I need to do this. And then the gradient-- yeah. So that's the gradient, of course. This is the gradient of F at K-- is that one. OK. So instead of this, let me just write what's happening if I'm tracking the coefficients CK plus 1 and DK plus 1.

Then what I really meant to have there is 1, 0. And minus S is a minus lambda. Is that right? Yeah. When I multiply the eigenvector by S, I'm just getting-- oh, it's a lambda times a CK. Yeah. Lambda times the CK-- that's good. I think that that's the left hand side of my equation. And on the right hand side, I have here. That's 1. And this was the scalar, the step size. And this was the other coefficient. It's the beta.

So I want to choose-- what's my purpose now? That gives me the-- what happens at every step to the C and D. So I want to choose the two things that I have-- I'm free to choose are S and beta. So that's my big job-- choose S and beta. OK. Now I-- to make-- oh, let me just shape this by multiplying the inverse of that, and get it over here. So that will really-- you'll see everything.

So CK plus 1, DK plus 1. What's the inverse of 1, 0? Oh, I don't think I want to-- that would have a tough time finding an inverse. It was a 1, wasn't it? Yeah. OK. So I'm going to multiply by the inverse of that matrix to get it over here. And what's the inverse of 1, 1 minus lambda? It's 1, 1 plus lambda. So that the inverse brought it over here, times this matrix, 1, 0 beta, and minus the step size. That's what multiply CK DK.

So we have these simple, beautiful steps which come from tracking one eigenvector-- makes the whole problem scalar. So I multiply those two matrices and I finally get the matrix that I really have to think about. 1, 0 times that'll be 1 minus S. Lambda 1 times that'll be a lambda there. And minus lambda S plus beta. Beta minus lambda S. That's the matrix that we see at every step. Let me call that matrix R.

So I've done some algebra-- more than I would always do in a lecture-- but it's really my-- I wouldn't do it if it wasn't nice algebra. What's the conclusion? That conclusion is that with the momentum term-- with this number beta available to choose, as well as S, the step-- the coefficient of the eigenvector is multiplied at every step by that matrix R. R is that matrix. And of course, that matrix involves the eigenvalue.

So we have to think about-- what do we want to do now? We want to choose beta and S to make R as small as possible, right? We want to make R as small as possible. And we are free to choose beta and S, but R depends on lambda. So I'm going to make it as small as possible over the whole range of possible lambdas. So let me-- so now here we really go.

So we have lambda between sum. These are the eigenvalue of S. And what we know-- what's reasonable to know-- is a lower bound. It's a positive. This is a symmetric positive definite matrix. A lower bound and an upper bound, for example, m was B, and M was 1, in that 2 by 2 problem. And this is what we know, that the eigenvalues are between m and M. And the ratio of m to M-- well, if I write-- this is the key quantity. And what's it called?

Lambda max divided by lambda min is the--

AUDIENCE: Condition number.

GILBERT STRANG: Condition number. Right. This is all sometimes written kappa-- Greek letter kappa-- the condition number of S. And when that's big, then the problem is going to be harder. When that's 1, then my matrix is just a multiple of the identity matrix. And the problem is trivial. When capital M and small m are the same, then that's saying that the largest and smallest eigenvalues are identical, that the matrix is a multiple of the identity. That's the condition number one.

But the bad one is when it's 1 over b, in our example, and that could be very large. OK. That's where we have our problem. Let me just insert about the ordinary gradient descent. Of course, the textbooks find a estimate for how fast that is. And of course, it depends on that number. Yeah. So it depends on that number, and you exactly saw how it depended on that number. Right.

But now we have a different problem. And we're going to finish it. OK. So what's my job? I'm going to choose S and beta to keep the eigenvalues of R. So let's give the eigenvalues of R a name. So R-- let's say R has eigenvalues e1, that depends on the lambda and the S and the beta and e2. So those are the eigenvalues of R-- just giving a letter to them. So what's our job? We want to choose S and beta to make those eigenvalues as small as possible. Right?

Small eigenvalues-- if R has small eigenvalues, its powers-- every step multiplies by R. So the convergence rate with momentum is-- depends on the powers of R getting small fast. It depends on the eigenvalues being small. We want to minimize the largest eigenvalue. So I'll say the maximum of e1 and e2-- that's our job. Minimize-- we want to choose S and beta to minimize the largest eigenvalue. Because if there's one small eigenvalue, but the other is big, then the other one is going to kill us.

So we have to get both eigenvalues down. And of course, those depend on lambda. E1 depends on lambda. So we have a little algebra problem. And this is what I described as a miracle-- the fact that this little algebra problem-- the eigenvalues of that matrix, e1 and e2, which depend on lambda in some way. And we want to make both e1 and e2 small-- the maximum of those-- of them. And we have to do it for all the eigenvalues lambda, because we have to-- we're now thinking-- we've been tracking each eigenvector.

So that gave us 1-- so this is for all possible lambda. So we have to decide, what do I mean by all possible lambda? And I mean all lambda that are between some m and M. There is a beautiful problem. You have a 2 by 2 matrix. You can find its eigenvalues. They depend on lambda. And what we-- all we know about lambda is it's between m and cap M. And also, they also depend on S and beta-- the two parameters we can choose.

And we want to choose those parameters, so that for all the possible eigenvalues, the larger of the two eigenvalues will be as small as possible. That's-- it's a little bit of algebra, but do you see that that's the tricky-- that-- I shouldn't say tricky, because it comes out-- this is the one that is a miracle in the simplicity of the solution. OK. And I'm going to-- in fact, maybe I'll move over here to write the answer. OK. And I just want to say that miracles don't happen so often in math.

There is-- all of mathematics-- the whole point of math is to explain miracles. So there is something to explain here, and I don't have my finger on it yet. Because-- anyway, it happens. So let me tell you what the right S, and the right beta, and the resulting minimum eigenvalue are. So again, they depend on little m and big M. That's a very nice feature, which we expect.

And they depend on the ratio. OK. So that ratio-- all right. Let's see it. OK. So the best S-- the S optimal has the formula 2 over square root of lambda max. That's the square root of M and the squared of m squared. Amazing OK. And beta optimal turns out to be the square root of M minus the square of little m, over the square root of M plus the square root of little m, all squared. And of course, we know what these numbers are-- 1 and beta, in our model problem.

That's where I'm going to get this square root of-- this is 1 minus the square root-- oh sorry, b. This is 1 minus the square root of b. In fact, for our example-- well, let me just write what they would be. 2 over 1 plus square root of b squared, and 1 minus square root of b over 1 plus square-- you see where this is-- 1 minus square root of b is beginning to appear in that.

It appears in this solution to this problem. And then I have to tell you what the-- how small do these optimal choices make the eigenvalues of R, right? This is what we're really paying attention to, because if the eigenvalues-- that matrix tells us what happens at every step. And its eigenvalues have to be small to get fast convergence. So how small are they? Well they involve this-- yeah. So it's the number that I've seen.

So in this case, the e's-- the eigenvalues of R-- that's the iterating matrix-- are below-- now you're going to see the 1 minus square root of b over 1 plus square root of b-- I think, maybe, squared. Let me just see. Yeah. It happens to come out that number again. So that's the conclusion. That with the right choice of S and beta, by adding this look back term-- look back one step-- you get this improvement. And it happens, and you see it in practice, of course. You'll see it exactly.

And so you do the job to use momentum. Now I'm going to mention what the Nesterov-- Nesterov had a slightly different way to do it, and I'll tell you what that is. But it's the same idea-- get a second thing. So let's see if I can find that. Yeah, Nesterov. OK. Here we go. So let me bring Nesterov's name down. So that's basically what I wanted to say about number 1.

And when you see Nesterov, you'll see that it's a similar idea of involving the previous time value. OK. There are very popular methods in use now for machine learning that involve-- by a simple formula-- all the previous values, by sort of a-- just by an addition of a bunch of terms. So it's really-- so it goes under the names adagrad, or others.

Those of you who already know about machine learning will know what I'm speaking about. And I'll say more about those. Yeah. But it doesn't involve a separate coefficient for each previous value, or that would be a momentous amount of work. So now I just want to tell you what Nesterov is, and then we're good. OK. Nesterov's idea. Let me bring that down. Shoot this up. Bring down Nesterov. Because he had an idea that you might not have thought of.

Somehow the momentum idea was pretty natural-- to use that previous value. And actually, I would like to know what happens if you use two previous values, or three previous values. Can you then get improvements on this convergence rate by going back two steps or three steps? If I'd use the analogy with ordinary differential equations, maybe you know. So there are backward difference formulas. Do you know about those for-- those would be in MATLAB software, and all other software.

Backward differences-- so maybe you go back two steps or four steps. If you're doing planetary calculations, if you're an astronomer, you go back maybe seven or eight steps to get super high accuracy. So that doesn't seem to have happened yet, but it's should happen here-- to go back more. But Nesterov has this different way to go back. So his formula is XK plus 1-- the new X-- is YK-- so he's introducing something a little different-- minus S gradient f at YK.

I'm a little surprised about that YK, but this is the point, here-- that the gradient is being evaluated at some different point. And then he has to give a formula for that to track those Y's. So the Y's are like the X's, but they are shifted a little bit by some term-- and beta would be fine. Oh no. Yeah-- beta-- have we got Nesterov here? Yes. Nesterov has a factor gamma in. Yeah. So all right. Let me try to get this right. OK. All right.

On a previous line, I've written the whole Nesterov thing. Here, let's see a Nesterov completely. And then it'll break-- then this is the step that breaks it into two first order. But you'll see the main formula here. XK plus 1 is XK. And then a beta times XK minus XK minus 1. So that's a momentum term. And then a typical gradient. But now here is Nesterov speaking up. Nesterov evaluates the gradient not at XK, not at XK minus 1.

But it his own, Nesterov point. So this is Nesterov's favorite point. Gamma XK minus XK minus 1. Some point, part way along that step. So this point-- because gamma is going to be some non-integer-- this evaluation point for the gradient of f is a little unexpected and weird, because it's not a mesh point. It's somewhere between. OK. Yeah. And then that-- so that involves XK plus 1, XK, and XK minus 1.

So it's a second order-- there's a second order method here. We're going to-- to analyze it, we're going to go through this same process of writing it as two first order steps-- two first-- two single step-- two one step from K to K plus 1 coupled with one step thing. Follow that same thing through, and then the result is, the same factor appears for him. The same factor-- this is also-- so the point is, this is for momentum and Nesterov, with some constant-- different by some constant.

But the key quantity is that one and that appears in both. So I don't propose, of course, to repeat these steps for Nesterov. But you see what you could do. You see that it involves K minus 1, KNK plus 1. You write it as-- you follow an eigenvector. You write it as a coupled system of-- that's a one step. That has a matrix. You find the matrix. You find the eigenvalues of the matrix.

You make those eigenvalues as small as possible. And you have optimized the coefficients in Nesterov. OK. That's sort of a lot of algebra that's at the heart of accelerated gradient descent. And of course, it's worth doing because it's a tremendous saving in the convergence rate. OK. Anybody running in the marathon or just watching? It's possible to run, you know. Anyway, I'll see you after the marathon, next Wednesday. And Professor Boyd will also see you.

Problem for Lecture 23
From textbook Section VI.4

5. Explain why projection onto a convex set \(K\) is a contraction in equation (24). Why is the distance \(||\boldsymbol{x}-\boldsymbol{y}||\) never increased when \(\boldsymbol{x}\) and \(\boldsymbol{y}\) are projected onto \(K\)?

Free Downloads

Video

• Internet Archive (MP4 - 109MB)

Caption

• English-US (SRT)