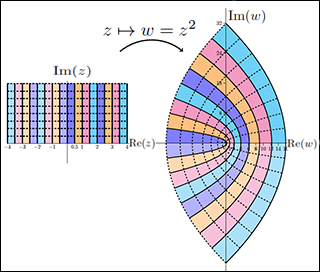
In the figure above, f(z) = z2 maps the first two quadrants to the entire plane. (Image courtesy of Jeremy Orloff.)
Instructor(s)
Jeremy Orloff
MIT Course Number
18.04
As Taught In
Spring 2018
Level
Undergraduate
Course Description
Course Features
Course Description
Complex analysis is a basic tool with a great many practical applications to the solution of physical problems. It revolves around complex analytic functions—functions that have a complex derivative. Unlike calculus using real variables, the mere existence of a complex derivative has strong implications for the properties of the function. Applications reviewed in this class include harmonic functions, two dimensional fluid flow, easy methods for computing (seemingly) hard integrals, Laplace transforms, and Fourier transforms with applications to engineering and physics.
Other Versions
Other OCW Versions
OCW has published multiple versions of this subject. ![]()
Archived versions: ![]()


