
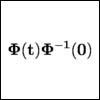 |
In this session we will learn the basic linear theory for systems. We will also see how we can write the solutions to both homogeneous and inhomogeneous systems efficiently by using a matrix form, called the fundamental matrix, and then matrix-vector algebra. |
Session Activities
Read the course notes:
Watch the lecture video clip:
- Theory of Systems (00:11:22)
Read the course notes:
- General Linear ODE Systems and Independent Solutions (PDF)
- The Existence and Uniqueness Theorem for Linear Systems (PDF)
- The Wronskian (PDF)
- Existence and Uniqueness and Superposition in the General Case (PDF)
Watch the lecture video clip:
- Fundamental Matrices (00:08:18)
Read the course notes:
Watch the lecture video clips:
- The Matrix Exponential I (00:26:26)
- The Matrix Exponential II (00:04:26)
Read the course notes:
Watch the lecture video clips:
-
Example: Solving a System with the Matrix Exponential (00:08:17)
Example: Solving a System with the Matrix Exponential
> Download from iTunes U (MP4 - 93MB)
> Download from Internet Archive (MP4 - 93MB)
- Calculating the Exponential Matrix (00:09:46)
- Variation of Parameters (00:13:19)
Read the course notes:
Watch the problem solving video:
- Matrix Exponentials (00:11:54)
Complete the practice problems:
Check Yourself
Complete the problem sets:
- Problem Set Part I Problems (PDF)
- Problem Set Part I Solutions (PDF)
- Problem Set Part II Problems (PDF)
- Problem Set Part II Solutions (PDF)
Session Activities
Watch the lecture video clip:
- Decoupling (00:47:06)
