Lecture 22: The z-Transform

Related Resources

The z-Transform (PDF)

• Download English-US transcript (PDF)

The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high-quality educational resources for free.

To make a donation, or view additional materials from hundreds of MIT courses, visit MIT OpenCourseWare at ocw.mit.edu.

[MUSIC PLAYING]

PROFESSOR: In the last several lectures, we've talked about a generalization of the continuous-time Fourier transform and a very similar strategy also applies to discrete-time, and that's what we want to begin to deal with in today's lecture. So what we want to talk about is generalizing the Fourier transform, and what this will lead to in discrete-time is a notion referred to as the z-transform.

Now, just as in continuous-time, in discrete-time the Fourier transform corresponded to a representation of a sequence as a linear combination of complex exponentials. So this was the synthesis equation. And, of course, there is the corresponding analysis equation. And as you recall, and as is the same for continuous-time, the reason that we picked complex exponentials was because of the fact that they are eigenfunctions of linear time-invariant systems.

In other words, if you have a complex exponential into a linear time-invariant system, the output is a complex exponential. And the change in complex amplitude, which corresponds to the frequency response, in fact is what led to the definition of the Fourier transform. In particular, it is the Fourier transform of the impulse response.

Well, that set of notions is, more or less, identical to the way we motivated the Laplace transform in the continuous-time case, in the Fourier transform in the continuous-time case. And just as in continuous-time, there are a set of signals more general than the complex exponentials, which are also eigenfunctions of linear time-invariant systems.

In particular, in discrete-time, if we had instead of an exponential e to the j omega n, we had a more general complex number z, that the signal z to the n is also an eigenfunction of a linear time-invariant system for any particular z. So we can see that by substituting that into the convolution sum and recognizing, again, very strongly paralleling the continuous-time argument, that we can rewrite this factor as z to the n z to the minus k.

And because of the fact that it's a sum on k and this term doesn't depend on k, we can take that term out. And the conclusion is that if we have z to the n as an input, that the output is of the same form times a factor which depends on z. But of course, doesn't depend on k because that is summed out as we form the summation.

So, in fact, this summation corresponds to a complex number, which we'll denote as H of z, where z will represent a more general complex number. Namely, z is r e to the j omega, r being the magnitude of this complex number and omega, of course, being the angle.

So for a linear time-invariant system, a more general complex exponential sequence of this form generates as an output a complex exponential sequence of the same form with a change in amplitude which we're representing as H of z, recognizing the fact that it's going to be a function of what that complex number is. And this amplitude factor is given by this summation. And it is this summation which is defined as the z-transform of the sequence H of n.

Now, let me stress that-- and I'll continue to stress this as the lecture goes on. That much of what we've said is directly parallel to what we said in the continuous-time case. And what we've simply done is to expand from complex exponentials with a purely imaginary exponent, complex exponential time functions or sequences of that form, to ones that have more general complex exponential factors.

Now, we have a mapping here from the impulse response to the amplitude or the eigenvalue associated with that input, and this mapping is what is referred to as the z-transform. So H of z is, in fact, the z-transform of the impulse response. And if we consider applying this mapping as we did in continuous-time in a similar argument, applying this mapping to a sequence whether or not it corresponds to the impulse response or a linear time-invariant system, that leads then to the z-transform of a general sequence x of n. The z-transform being defined by this relationship.

And again, notationally, we'll often represent a time function and a z-transform through a shorthand notation, just indicating that x of z is the z-transform of x of n.

So we've kind of motivated the development in a manner exactly identical to what we had done with the Laplace transform. Kind of the idea that if you look at the eigenvalue associated with a linear time-invariant system, that essentially generates a mapping between the sequence-- system impulse response and a function of z. And that corresponds to the z-transform here, it corresponded to the Laplace transform in the continuous-time case.

That same argument is also the kind of argument that we use to lead us into the Fourier transform originally. And once again, what you would expect is that the z-transform has a very close and important relationship to the Fourier transform. And indeed, that relationship turns out to be, more or less, identical to the relationship between the Laplace transform and the Fourier transform in continuous-time.

Well, let's look at the relationship. First of all, what we recognize is that if we compare the Fourier transform expression for a sequence and the z-transform expression for the same sequence that they involve, essentially, the same operations. And in fact, since z is of the form r e to the j omega, if we want this sum to look like this sum, then that would mean that we would choose z equal to e to the j omega.

Said another way, the z-transform, when z is e to the j omega, is going to reduce to the Fourier transform. So we have a relationship like the one, again, that we had between the Laplace transform and the Fourier transform in continuous-time. Namely that for a certain set of values of the complex variable, the transform, the z-transform, reduces to the Fourier transform.

So if we have x of z, the z-transform, and we look at that for z equal to e to the j omega, and z equal to e to the j omega is similar to saying that we're looking at that for the magnitude of z equal to 1. We're specifically choosing r equal to 1, which is the magnitude of z. Then this is equal to the Fourier transform of the sequence. So the z-transform for z equal to e to the j omega is the Fourier transform, and so this then corresponds to x of omega. Namely, the Fourier transform.

Well, we now have ourselves in a similar situation, again, to what we had when we talked about the Laplace transform. Namely, a notational awkwardness, or inconvenience, which we can resolve by simply redefining some of our notation. In particular, the awkwardness relates to the fact that whereas we've been writing our Fourier transforms this way, as x of omega, if we were to express x of z and look at it, it's equal to e to the j omega. We end up with the independent variable being e to the j omega rather than omega.

Well, in fact, the Fourier transform is a function of omega. It's also a function of e to the j omega. And now what we can see is that given the fact that we want to generalize the Fourier transform to the z-transform, it's convenient now to use as notation for the Fourier transform x of z with z equal to e to the j omega. Namely, our Fourier transforms will now be written as I've indicated here.

So just summarizing that, our new notation is that the independent variable on the Fourier transform is now going to be expressed as e to the j omega rather than as omega. It's a minor notational change, but I recognize the fact that it's somewhat confusing initially, and takes a few minutes to sit down and just get it straightened out. It's very similar to what we did with the Laplace transform.

But let me draw your attention to the fact that in the Laplace transform, the independent variable that we ended up with in talking about the Fourier transform is different than what we're ending up with here. In particular, before we had j omega, now we have e to the j omega. And the reason for that is simply that whereas in continuous time we were talking about functions of the form e to the st, now we're talking about sequences of the form z to the n.

So we have one relationship between the Fourier transform and the z-transform. Namely, the fact that for the magnitude of z equal to 1, the z-transform reduces to the Fourier transform.

Now, in the Laplace transform, we also had another important relationship and observation, which was the fact that the Laplace transform was the Fourier transform of x of t modified. And how was it modified? It was modified by multiplying by a decaying or growing exponential, depending on what the real part of s is.

Well, we have a very similar situation with the z-transform. In particular, in addition to the fact that the z-transform for z equal to e to the j omega reduces to the Fourier transform, we'll see that the z-transform for other values of z is the Fourier transform of the sequence with an exponential weighting. And let's see where that comes from.

Here we have the general expression for the z-transform. And recognizing that z is a complex number which we're expressing in polar form as r e to the j omega, substituting that in, this summation now becomes x of n, r e to the j omega to the minus n. We can factor out these two terms, r to the minus n and e to the minus j omega n. And combining the r to the minus n with x of n and the e to the minus j omega n being treated separately, what we end up with is the summation that I have here.

Well, what this says is that the z-transform, which is this, at z equal to r e to the j omega, is in fact the Fourier transform of what? It's the Fourier transform of x of n multiplied by r to the minus n. So that is the expression that we have here.

And in continuous-time, we had the Laplace transform as the Fourier transform of x of t e to the minus sigma t. Here we have the Fourier transform of x of n r to the minus n.

Now, something to just reflect on for a minute is-- because it tends to cause a little bit of problem with the algebra later on if you're attention isn't drawn to it, is that we're talking about multiplying x of n times r to the minus n. The question is, for r greater than 1, does r to the minus n increase exponentially as n increases or does it decrease?

We're talking about r to the minus n. If r is greater than 1, if the magnitude of r is greater than 1. For example, if it's equal to 2, r to the minus n is 1/2 to the n. And so, in fact, that decreases exponentially. Or more generally, the larger r is, the faster r to the minus n decays with increasing n.

Well, let's just look at some examples of the z-transform. And examples that I've picked, again, are examples directly out of the text. And so the details of the algebra you can look at more leisurely as you sit with the textbook.

Let's consider, first of all, an exponential sequence x of n equals a to the n times the unit step. So 0 for negative time and an exponential for positive time. And the Fourier transform, as we've seen in earlier lectures, is 1 over 1 minus a e to the minus j omega. But this doesn't always converge. In particular, for convergence of the Fourier transform, we would require absolute summability of the original sequence. And that, in turn, requires that the magnitude of a be less than 1.

So the Fourier transform is this, provided that the magnitude of a is less than 1. And what is the Fourier transform if the magnitude of a is not less than 1?

Well, the answer is that, in that case, it doesn't converge.

Now, let's look at the z-transform. The z-transform is the sum from minus infinity to plus infinity of a to the n z to the minus n times the unit step. The unit step will change the lower limit to 0. So it's the sum from 0 to infinity. And this is of the form a times z to the minus 1 to the n. So we're summing from 0 to infinity a times z to the minus 1 to the n. That sum is 1 over 1 minus a z to the minus 1. But in order for that sum to converge, we require that the magnitude of a times z to the minus 1 be less than 1.

Now, the z-transform is the Fourier transform of the sequence a to the n times r to the minus n. And this statement about the z-transform converging is exactly identical to the statement that what we're requiring is that the magnitude of a times r to the minus 1 be less than 1, where this represents the exponential factor that we have that in effect is applied to the sequence, so that the Fourier transform becomes the z-transform. And so, if we put this condition, we can interpret this condition in exactly the same way that we interpret the condition on convergence of the Fourier transform.

So from what we've worked out here then, what we have is the z-transform of a to the n times u of n is 1 over 1 minus a z to the minus 1. That works for any value of a provided that we pick the value of z correctly. In particular, we have to pick the set of values of z, so that what? So that the magnitude of a times z to the minus 1 is less than 1. Or equivalently, so that the magnitude of z is greater than the magnitude of a.

So associated with the z-transform of this sequence is this algebraic expression, and this set of values on z for which that algebraic expression is valid. And just as with the Laplace transform, this range of values is referred to as the region of convergence of the z-transform.

Now, again, as we saw with the Laplace transform, it's important to recognize that in specifying or having worked out the z-transform of a sequence, it's not just the algebraic expression, but also the region of convergence that's required to uniquely specify it.

To emphasize that further, here is Example 10.2 from the text. And if you work that one through, what you find is that, algebraically, the z-transform of this sequence is 1 over 1 minus a z to the minus 1. Identical algebraically to what we had up here. But now with a region of convergence, which is the magnitude of z less than the magnitude of a. In contrast to this example, where the region of convergence was the magnitude of z greater than the magnitude of a.

So again, it requires not just the algebraic expression, but also requires a specification of the region of convergence. And also, as with the Laplace transform, it's convenient in looking at the z-transform to represent it in the complex plane. In this case, the complex plane referred to as the z-plane, whereas in continuous-time when we talked about the Laplace transform, it was the s-plane. z, of course, because z is the complex variable in terms of which we're representing the z-transform.

So we will be representing the z-transform in terms of representations in the complex plane, real part and imaginary part. But I've also identified a circle here. And you could wonder, well, what's the significance of the circle?

Recall that in the discussion that we just came from, when we talked about the relationship between the z-transform and the Fourier transform, the z-transform reduces to the Fourier transform when the magnitude of z is equal to 1. The magnitude of z equal to 1 in the complex plane is a circle. And that circle, in fact, is a circle of radius 1. And so it's on this contour in the z-plane that the z-transform reduces to the Fourier transform. And we'll see some additional significance of that as we go along.

Just again to emphasize the relationships and differences with continuous-time, with the Laplace transform it's the behavior in the s-plane on the j omega axis that corresponds to the Fourier transform. Here it's the behavior on the unit circle where the z-transform corresponds to the Fourier transform.

Now, we'll be talking-- as we did with the Laplace transform, we'll be talking very often about transforms which are rational, and rational transforms as we'll see, represent systems which are characterized by linear constant coefficient difference equations. And so for the rational z-transforms, we'll again find it convenient to use a representation in terms of poles and zeroes in the z-plane.

So let's look at our example as we've worked it out previously, Example 10.1. And with this sequence, the z-transform is 1 divided by 1 minus a z to the minus 1. And we happen to have written it as a function of z to the minus 1. Clearly, we can rewrite this by multiplying numerator and denominator by z, and this would equivalently then be z divided by z minus a.

And so if we were to represent this through a pole-zero plot, we would have a 0 at the origin corresponding to this factor and a pole at z equals a corresponding to the denominator factor. And so the pole-zero pattern for this is then a pole at z equal to a and a 0 at the origin.

Now, let me just comment quickly about the fact that we had written this as 1 over 1 minus a z to the minus 1, and that seems kind of strange because perhaps we should have multiplied through by z. Let me just indicate that as you'll see as you work examples, it's very typical for the z-transform to come out as a function of z to the minus 1. And so very typically, you'll get to recognize that things will be expressed in terms of factors involving terms like 1 minus a z to the minus 1, rather than factors of the form z minus a.

Well, here is the one example that we had referred to. And if we consider another example, the other example, which was example 10.2 consists of an algebraic expression as I indicate here. But its region of validity is the magnitude of z less than the magnitude of a. And that corresponds to the same pole-zero plot, but a region of convergence which is inside this circle.

Whereas, in the previous case, with the pole-zero plot, we had a region of convergence which was for the magnitude of z greater than the magnitude of a. So these two examples, this one and the other one, have exactly the same pole-zero pattern and they're distinguished by their region of convergence.

Now, notice incidentally that in this particular case, the region of convergence includes the unit circle provided that the magnitude of a is less than 1. And so, in fact, that would say that the sequence has a Fourier transform that converges. Namely, with the magnitude of z equal to 1. Whereas, in this example, the region of convergence does not include the unit circle. And so, in fact, we cannot look at x of z for the magnitude of z equal to 1. And so this example, with the magnitude of a less than 1, does not have a Fourier transform that converges.

Well, assuming that the magnitude of a is less than 1 and the Fourier transform converges, we can, in fact, look at the Fourier transform by observing what happens as we go around the unit circle. We had seen this with the Laplace transform in terms of observing what happened as we move along the j omega axis. And here again, we can use the vectors as we trace out the unit circle. And in particular, what we would be looking at in this case is the ratio of the zero vector to the pole vector.

For example, if we were looking at the magnitude of the z-transform, the magnitude of the z-transform would be the ratio of the length of this vector to the length of this vector. And to observe the Fourier transform, we would observe how those vectors change in length as we move around the unit circle. And as we move around the unit circle, what we would trace out in terms of the ratio of the lengths of those vectors is the Fourier transform.

Well, let's focus on that also in the context of a slightly different z-transform. In the z-transform here as we'll see in a later lecture, is the z-transform associated with a second order difference equation. It has a denominator factor which has two poles associated with it.

And so here, if we assumed that the Fourier transform of the associated sequence converged, then again we would look at the behavior of this as we moved around the unit circle. And the ratio of the lengths of the appropriate vectors would describe for us the frequency response. I'm sorry, the Fourier transform.

So the Fourier transform magnitude would consist of the ratio of the lengths of the zero vectors divided by the lengths of the pole vectors. And one thing that we observe is that as we move in frequency omega in the vicinity of this pole, this pole vector, in fact, reaches a minimum length. That would mean that it's reciprocal would be maximum. And then, as we sweep past, the lengths of these two vectors would increase. The zero vectors, of course, would retain the same length no matter where we were on the unit circle.

So, in fact, if we looked at the Fourier transform associated with this pole-zero pattern, if this was, for example, represented the z-transform of the impulse response or a linear time-invariant system, the corresponding frequency response would be what I plotted out below. And so it would peak. And in fact, where it would peak is in the vicinity of the frequency location of the pole as I indicate up here. So as we sweep past this pole then, in fact, this Fourier transform . Peaks.

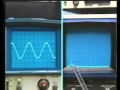
Well, this notion of looking at the frequency response as we move around the unit circle is a very important notion. And it's important to recognize it's the unit circle we're talking about here, whereas before we were talking about the j omega axis. And to emphasize this further, let me just show this example. And in fact, the previous example with the computer displays, so that we can see the frequency response as it sweeps out as we go around the unit circle.

So here we have the pole-zero pattern for the second order example. And to generate the Fourier transform, we want to look at the behavior of the pole and zero vectors as we move around the unit circle. So first, let's display the vectors. And here we have them displayed to the point corresponding to zero frequency. And the magnitude of the Fourier transform will be, as we discussed, the magnitude of the length of the zero vector is divided by the magnitude of the length of the pole vectors.

Shown below will be the Fourier transform. And we have the Fourier transform displayed here from 0 to 2 pi, rather than from minus pi to pi as it was displayed in the transparency. Because of the periodicity of the Fourier transform, both of those are equivalent.

Now we're sweeping away from omega equals 0 and the lengths of the pole vectors have changed. And that, of course, generates a change in the Fourier transform. And as we continued the process further, if we increase frequency, as we sweep closer to the location of the pole, the pole vector decreases in length dramatically. And that generates a residence in the Fourier transform, very similar to what we saw in continuous-time.

Now as we continue to sweep further, what will happen is that that pole vector will begin to increase in length again. And so, in fact, the magnitude of the Fourier transform will decrease. And we see that here as we sweep toward omega equal to pi.

Now, notice in this process that the length of the zero vectors has stayed the same because of the fact that the zeroes are at the origin, and no matter where we are in the unit circle, the length of those vectors is unity. So they don't influence in this example the magnitude, but they would, of course, influence the phase.

Now we want to continue sweeping from omega equal to pi around to 2 pi. And because of the symmetry in the Fourier transform, what we will see in the magnitude is identical to what we would see if we swept from omega equal to pi back clockwise to omega equals 0.

In particular now, as we're increasing frequency, notice that the length of the pole vector associated with the lower half plane pole is decreasing. And so, in fact, that corresponds to generating a resonance as we sweep past that pole location as we are here.

And then finally, that pole vector increases in length as we begin to approach omega equal to 2 pi. Or equivalently, as we approach omega equal to 0.

Now finally, let's also look at the Fourier transform associated with the first order example that we discussed earlier in the lecture. And so what we'll want to look at is the Fourier transform as the pole and zero vectors change. Once again, the Fourier transform will be displayed on a scale from 0 to 2 pi, a frequency scale from 0 to 2 pi, rather than minus pi to pi. And we want to observe the pole and zero vectors as we sweep around the unit circle.

We display first the pole and zero vectors at omega equal to 0. And as the frequency increases, the pole vector increases in length. The zero vector, since the zero is at the origin, will have constant length no matter where we are on the unit circle. Although it would affect the phase, which we are not displaying here. And so the principle effect, the only effect really on the magnitude, is due to the pole vector.

As the frequency continues to increase, the pole vector increases in length, monotonically in fact. And so that means that the magnitude of the Fourier transform will decrease monotonically until we get past omega equal to pi.

Here we are now at omega equal to pi. And when we continue sweeping past this frequency around to 2 pi, then we will see basically the same curve swept out in reverse. Since because of the symmetry, again, of the Fourier transform magnitude, sweeping from pi to 2 pi is going to be equivalent with regard to the magnitude to sweeping from pi back to 0.

And so now the pole vector begins to decrease in length and correspondingly, the magnitude of the Fourier transform will increase. And that will continue until we get around to omega equal to 2 pi, which is equivalent, of course, to omega equal to 0. And obviously, if we continue to sweep around again, we would simply trace out other periods associated with the Fourier transform.

Well, that hopefully gives you kind of some feel for the notion of sweeping around the unit circle. And of course, you can see that because the circle is periodic as we go around and around, of course, what we'll get is a periodic Fourier transform, which is the way Fourier transforms are supposed to be.

Now, just as with the Laplace transform, the region of convergence of the z-transform, as we've seen in this example, is a very important part of the specification of the z-transform. And we can, in talking about sequences and their transforms, either specify the region of convergence implicitly, or we can specify it explicitly.

We can, for example, say what it is, as let's say the magnitude of z being greater than the magnitude of a. Or we can recognize that the region of convergence has certain constraints associated with certain properties of the time function. And in particular, there are some important properties of the region of convergence which allow us, given that we know certain characteristics of the time function, to then identify the region of convergence by looking at the pole-zero pattern.

For example, we recognize that the region of convergence does not contain any poles because of the fact that at poles, the z-transform, in fact, blows up and, of course, can't converge at that point.

Furthermore, the region of convergence consists of a ring in the z-plane centered about the origin. Recall that with the Laplace transform, the region of convergence consisted of strips in the s-plane. With the z-transform, the region of convergence consists of a ring, basically because of the fact that the region of convergence is dependent on the magnitude of z. Whereas, with the Laplace transform, the region of convergence was dependent on the real part of s. The fact that it's the magnitude of z says, in effect, that all values of z that have the same magnitude lie on a circle. And so the region of convergence you would expect to be a concentric ring in the z-plane.

Furthermore, as we've already talked about and exploited actually, convergence of the Fourier transform is equivalent to the statement that the region of convergence includes the unit circle in the z-plane.

Now, we can also associate the region of convergence with issues about whether the sequence is of finite duration or right-sided or left-sided. And let me sort of quickly indicate again what the style of the argument is.

If we have a finite duration sequence, so that the sequence is absolutely summable, and therefore has a Fourier transform that converges, then because of the fact that it's 0 outside some interval, I can multiply it by an exponentially decaying sequence or by an exponentially growing sequence. And since I'm only doing this over a finite interval, no matter how I choose that exponential, we'll end up with an absolutely summable product.

So if x of n is a finite duration, then in fact the region of convergence is the entire z-plane, possibly with the exception of the origin or infinity.

On the other hand, if the sequence is a right-sided sequence, then we have to be careful that we don't multiply by an exponential that grows too fast for positive time. Or equivalently, we might have to choose the exponential so that it decays sufficiently fast for positive time.

As a consequence of that, for a right-sided sequence, if we have a value which is in the region of convergence, as long as I multiply by exponentials that decay faster than that for positive time, then I'll also have convergence. In other words, all finite values of z for which the magnitude of z is greater than this, so that the exponentials die off even faster will also be in the region of convergence.

If we combine that statement with the fact that there are no poles in the region of convergence, then we end up with a statement similar to what we had with the Laplace transform. Here, the statement is that if the sequence is right-sided, then the region of convergence has to be outside the outermost pole. Essentially, because it has to be outside someplace and can't include any poles.

Finally, if we have a left-sided sequence, then if we have a value which is in the region of convergence, all values for which the magnitude of z is less than that will also be in the region of convergence. Or if x of z is rational, then the region of convergence must be inside the innermost pole. And finally, if we have a two-sided sequence, then there's kind of a balance between the exponential factor that we use. And so in that case, then the region of convergence will be a ring in the z-plane, and essentially will extend outward to a pole and inward to a pole.

So if we had an algebraic expression, let's say as we have here, then we could associate with that a region of convergence outside this pole. And that would correspond to a right-sided sequence. Or we can associate with it a region of convergence, which is inside the innermost pole. And that would correspond to a left-sided sequence. And the third and only other possibility is a region of convergence which lies between these two poles. And that would then correspond to a two-sided sequence.

And notice incidentally because of where I've placed these poles, that this is the only one for which the region of convergence includes the unit circle. In other words, it's the only one for which the Fourier transform converges.

OK, now we've moved through that fairly quickly. And I've emphasized the fact that it parallels very closely what we did with the Laplace transform. What I'd like to do is just conclude with a discussion of how we get the time function back again when we have the z-transform including its region of convergence.

Well, we can, first of all, develop a more or less formal expression. And the algebra for this is gone through in the text, and you went through something similar to this with the Laplace transform in the video course manual. So I won't carry through the details. But basically, what we can use to develop a formal expression is the fact that the z-transform is the Fourier transform of the sequence exponentially weighted.

So we can apply the inverse transform to that, and that gives us not x of n, but x of n exponentially weighted. And if we track that through, then what we'll end up with is an expression. After we've taken care of a few of the epsilons and deltas, we'll end up with an expression that expresses formally the sequence x of n in terms of the z-transform, where this, in fact, is a contour integral in the complex plane.

And so there's a formal expression, just as there's a formal expression for the Laplace transform. But in fact, the more typical procedure is to use essentially transformed pairs that we know together with the idea of using a partial fraction expansion.

So if we had a z-transform as I indicate here, and if we expand it out in a partial fraction expansion, then we can recognize, as we did in a similar style with the Laplace transform-- we can recognize that each term, together with the identified region of convergence corresponds to an exponential factor. And so this term, together with the fact we know that the magnitude of z must be greater than 2, allows us to recognize this as similar to the Example 10.1. And in particular then, the sequence associated with that is what I indicate here. And for the second term, the sequence is what I indicate here.

So what we're simply doing is using the fact that we've worked out the example going one direction before, and now we use that together with the partial fraction expansion to get the individual sequences back again, and then add them together.

There's one other method which I'll just point to, which is also elaborated on a little more in the text. But it's kind of the idea of developing the inverse z-transform by recognizing that this z-transform formula, in fact, is a power series. So if we take x of z and expand it in a power series, then we can pick off the values of x of n by identifying the individual coefficients in this expansion.

And so by simply doing long division, for example, we can also get the inverse transform. And that, by the way, is very useful. Particularly if we want to get the inverse z-transform for a z-transform expression, which is not rational.

Now we've moved through this fairly quickly. On the other hand, I've stressed that it's very similar to what we went through for the Laplace transform, except for a very important difference. The principal difference really being that with the Laplace transform, it was the j omega axis in the s-plane that we focused attention on when we were thinking about the Fourier transform. Here, the unit circle in the z-plane plays an important role.

What we'll see when we continue this in the next lecture is that there are properties of the z-transform, just as there were properties of the Laplace transform. And those properties allow us to develop and exploit the z-transform in the context of systems describable by linear constant coefficient difference equations.

So in the next lecture, we'll focus on some properties of the z-transform, and then we'll see how to use those properties to help us in getting further insight and working with systems describable by difference equations. Thank you.

Free Downloads

Video

• iTunes U (MP4 - 112MB)
• Internet Archive (MP4 - 112MB)

Caption

• English-US (SRT)