Flash and JavaScript are required for this feature.
Download the video from iTunes U or the Internet Archive.
Topics covered: Course format and overview; Demonstration of a feedback system used to stabilize an inverted pendulum; Demonstration of digital signal processing used to remove distortions and background noise from a musical recording. Mathematical representation of signals and systems.
Instructor: Prof. Alan V. Oppenheim

Lecture 1: Introduction
Related Resources
Introduction (PDF)
[MUSIC PLAYING]
PROFESSOR: I'm Al Oppenheim, and I'd like to welcome you to this videotape course on signals and systems. Signals, at least as an informal definition, are functions of one or more independent variables that typically carry some type of information. Systems, in our setting, would typically be used to process signals.
One very common example of a signal might be, let's say, a speech signal. And you might think of the air pressure as a function of time, or perhaps the electrical signal after it goes through the microphone transducer as a function of time, as representing the speech signal. And we might see a typical speech signal looking something like I've indicated here.
It's a function of time, in this particular case. And the independent variable, being time, is, in fact, continuous. And so a signal like this, we will typically be referring to as a continuous time signal.
Now, it also, for this particular example, is a function of one independent variable. And that will be referred to as a one-dimensional signal corresponding to the fact that there's only one independent variable instead of several independent variables. So the speech signal is an example of a continuous time, one-dimensional signal.
Now, signals can, of course, be multi-dimensional. And they may not have, as their independent variables, time variables. One very common example are the examples represented by images.
Images, as signals, we might think of as representing brightness, as it varies in a horizontal and vertical direction. And so the brightness as a function of these two spatial variables is then a two-dimensional signal. And the independent variables would typically be continuous, but of course they're not time variables. And incidentally, it's worth just commenting that very often, simply for convenience, we'll have a tendency to refer to the independent variables when we talk about signals as time variables, whether or not they really do represent time.
Well, let me illustrate one example of an image. And this is a picture of J. B. J. Fourier, who, perhaps, more than anyone else, is responsible for the elegance and beauty of a lot of the concepts that we'll be talking about throughout this course. And when you look at this, in addition to seeing Fourier himself, you should recognize that what you're looking at is basically a signal which is brightness as a function of the horizontal and vertical spatial variables.
As another example of an image as a signal, let's look at an aerial photograph. This is an aerial photograph taken over a set of roads, which you can more or less recognize in the picture. And one of the difficulties with this signal is that the road system is somewhat obscured by cloud cover. And what I'll want to show later as an example of what a system might do to such a signal, in terms of processing it, is an attempt to at least compensate somewhat for the cloud cover that's represented in the photograph.
Although in terms of the detailed analysis that we go through during the course, our focus of attention is pretty much restricted to one-dimensional signals. In fact, we will be using two-dimensional signals, more specifically images, very often to illustrate a variety of concepts.
Now, speech and images are examples of what we've referred to as continuous-time signals in that they are functions of continuous variables. An equally important class of signals that we will be concentrating on in the course are signals that are discrete-time signals, where by discrete-time, what we mean is that the signal is a function of an integer variable, and so specifically only takes on values at integer values of the argument. So here is a graphical illustration of a discrete-time signal.
And discrete-time signals arise in a variety of ways. One very common example that is seen fairly often is discrete-time signals in the context of economic time series, for example, stock market analysis. So what I show here is one very commonly occurring example of a discrete-time signal. It represents the weekly stock market index.
The independent variable in this case is the week number. And we see what the stock market is doing over this particular period as a function of the number of the week. And, of course, along the vertical axis is the weekly index.
Incidentally, this particular period was not chosen at random. It In fact captures a very interesting aspect of stock market history, namely the stock market crash in 1929, which, in fact, is represented by the behavior of this discrete-time signal, or sequence, in this particular area. So this dramatic dip, in fact, is the stock market crash of 1929.
Well, the Dow Jones weekly average is an example of a one-dimensional discrete-time signal. And just as with continuous time, we had not just one-dimensional but multi-dimensional signals, likewise we have multi-dimensional signals in the discrete-time case where, in that case, then, the discrete-time signal that we're talking about, or sequence, is a function of two integer variables. And as one example, this might, let's say, represent a spatial antenna array where this is array number in, let's say, the horizontal direction, and this is array number in the vertical direction.
Both classes of signals, continuous-time and discrete-time, as I've indicated, are very important. And it should be emphasized that the importance of discrete-time signals and associated processing continues to grow in large part because of the current and emerging technologies that permit, basically, the processing of continuous-time signals by first converting them to discrete-time signals and processing them with discrete-time systems. And that, in fact, is a topic that we will discuss in a fair amount of detail later on in the course.
Let's now our attention to systems. And as I indicated, a system basically processes signals. And they have, of course, inputs and outputs. And depending on whether we're talking about continuous time or discrete time, the system may be a continuous-time system or a discrete-time system.
So in the continuous-time case, I indicate here an input x(t) and an output y(t) If we were talking about a discrete-time system, I would represent the input in terms of a discrete-time variable, and, of course, the output in terms of a discrete-time variable also. Now, in very general terms, systems are hard to deal with because they are defined very broadly and very generally. And in dealing with systems and analyzing them, what we will do is attempt to exploit some very specific, and as we'll see, very useful system properties.
To indicate what I mean and how things might be split up, we could talk about systems, and will talk about systems, that are linear. And we could divide systems, basically, into systems that are either linear or nonlinear, and we will, and also divide systems into systems that are what we'll refer to as time-invariant or time-varying systems. And these aren't terms that we've defined yet, of course, but we will be defining in the course very shortly.
And while, in some sense, this division represents all systems, and this does, too, the focus of the course is really going to be principally on linear, time-invariant systems. So it's basically these systems that we will be focusing on. And we'll be referring to those systems as linear, time-invariant systems.
Well, as a brief glimpse at some of the kinds of things that systems can do, let me illustrate, first in a one-dimensional continuous-time context, and then later with a discrete-time example, one example of some processing of signals with an appropriate system. The particular example that I want to illustrate relates to the restoration of old recordings. And this is some work that was done by Professor Thomas Stockham, who is at the University of Utah, and work that he had done a number of years ago relating to the fact that in old recordings, for example in Caruso recordings, the recording was done through a mechanical horn, and the characteristics of the horn tended to vary from day to day. And because of the characteristics of the horn, the recording tended to have a muffled quality, something like this, sort of the sense that you would get if you were speaking through a megaphone.
What Professor Stockham did was develop a system to process these old recordings in such a way that a lot of the characteristics and distortion due to that recording system was removed. So I'd like to illustrate that as one example of some signal processing with an appropriate continuous-time system. And what you'll hear is a two-track recording. On the first track is the original, unrestored Caruso recording, and on the second track is the result of the restoration. And so as I switch back and forth from channel one to channel two, we'll be switching from the original to the restored.
We'll begin the tape by playing the original. And then, as it proceeds, we'll switch. So we'll begin on channel one.
[MUSIC PLAYING, MUFFLED]
That's the original recording. And switch now to the processed.
[MUSIC PLAYING, CLEARER]
Now let's switch back, back to the original. Back to the restoration. And once again, back to the original.
And presumably and hopefully, what you heard was that in the restoration, in fact, a lot of the muffled characteristics of the original recording were compensated for or removed. Now one of the interesting things that happened, in fact, in the work that Professor Stockham did is that in the process of the restoration-- and perhaps you heard this-- in the process of the restoration, in fact, some of the background noise on the recording was emphasized. And so he processed the signal further in an attempt to remove that background noise.
And with that particular processing, the processing was very highly nonlinear. A very interesting thing happened, which was that not only in that processing was the background noise removed, but somewhat surprisingly, also the orchestra was removed. And let me just play that now as an example of some very sophisticated processing with a nonlinear system.
What you'll hear on channel one is the restoration as we had just played it. When I switch to channel two, it will be after the processing with an attempt to remove the orchestra and the background noise. Channel one now. And now the noise and orchestra removed. Back to channel one. And finally, once again, with the orchestra removed.
So that's an example of processing of a continuous-time signal with a corresponding continuous-time system. Now I'd like to illustrate an example of some processing on a discrete-time signal. And I'd like to do that in the context of the example that I showed before of a discrete-time signal, which was the Dow Jones Industrial weekly stock market index.
I had shown it before, as I've shown it here again, over a period of slightly more than a year, where this is the number of weeks and this is the weekly index. And to illustrate some of the processing, what I'd like to do is show the stock market index, the weekly index, over a much longer time period, in particular, the weekly index over a 10 year period. And that's what I show here.
So what this covers is roughly 1927 to 1937. And in this case, although this is still a discrete-time signal, just simply for the purposes of display, what we've done is to essentially connect the dots and draw a continuous curve through the points so that this picture isn't filled up with a lot of vertical lines. So this is the discrete-time sequence that represents the weekly Dow Jones Index over a 10 year period.
And here, by the way, again, is the crash of 1929. It's interesting to note, by the way, that actually the disaster in the stock market wasn't so much the 1929 crash but the long downward trend that followed that. And you can see that here by filtering through, by eye, the rapid variations in the index. And what you see is this smooth downward trend followed, eventually, by an upward trend.
Now, this issue of looking at something like this, looking at a sequence, and following the smoother parts of it, namely the long term trends, is, in fact, something that is done quite typically with economic time series like this. And in particular, what's done is to smooth it, or average over some time period, to emphasize the slow variations and de-emphasize the rapid variations. And that, in fact, is processing that is done with a discrete-time system.
So when you hear referred to, let's say, in stock market reports, a 51-day moving average, that, in fact, is processing the stock market index with a particular discrete-time system. The result of doing that on this particular example generates a smooth version of the curve, which I overlay here. And the overlay, then, is really attempting to track the smoother variations and de-emphasize the more rapid variations.
Let me just slightly offset that so that the difference stands out a little more. And so here you see what is the original weekly index. And this is the result of processing that sequence with an appropriate system to apply smoothing. And in fact, what it is is a moving average. And so here again, you can see, in the smoother curve, this general downward trend up until this time period, followed by, eventually, a recovery.
Well, we've seen an example with a continuous-time signal, the Caruso recording, an example of the discrete-time signal, this stock market index. And what I'd also like to show is a third example, which is the result of some processing on an image, in particular the image that we talked about before, which was the aerial photograph that had the problem of some cloud cover.
So once again, what we see here is the original aerial photograph with the cloud cover. And some processing was applied to this using a system which, in fact, was both nonlinear and quote "time-varying," or, in the case of these independent variables, we would refer to it as spatially-varying. And the result of applying that processing is shown in the adjoining picture. And what we see there is hopefully a reasonable attempt to compensate for the cloud cover.
And this, by the way, was some work that was done by Professor Lim at MIT, and has been very successful type of processing for aerial photographs. I should say, also, that this particular example is one where, although the original signal was a signal that is continuous-time, that is, the independent variables are continuous, as they are in a spatial, aerial photograph, in fact, for the processing, that picture was first converted to a sequence through a process called sampling, which we'll be talking about later. And then the processing, in fact, was done on a digital computer.
Well, these then are some examples of the use of some systems to process some signals, both in continuous time and discrete time, for one-dimensional signals and for multi-dimensional signals. And as I've referred to systems, we've thought of them as one big block with an appropriate, or associated, input and output. And as we'll be getting into in the first part of the course, very often, systems are interconnected together for a variety of reasons.
Some of the kinds of interconnections that we'll talk about are connecting systems in what are called series, or cascade interconnections, parallel interconnections, feedback interconnections. And feedback interconnections, in fact, are very interesting, very important, and very useful, and will be a major topic toward the end of the course.
Feedback, as you may or may not know, comes into play in a variety of situations, for example, in amplifier design, as we'll talk about, feedback plays an important role. In a situation where you have a basically unstable system, feedback is often used to stabilize the system. And feedback interconnections of systems in that sense are very often used in high performance aircraft, which are inherently unstable, and are stabilized through this kind of interconnection.
Just to give you a little sense of this without going into any of the details, what I'd like to show you is an excerpt from a lecture that we'll be seeing toward the end of the course relating to the analysis of feedback systems and the uses of feedback. And this is in the context of what's referred to as the inverted pendulum, which is a system that's basically unstable, and feedback interconnections are used to stabilize it. The idea, as you'll see in this brief clip, is that there is a cart that's moving on a track with a rod that's pivoted at the base.
And so that system, in the absence of anything, is unstable in that the rod would tend to fall. And as we go into in detail in the lecture later, we use feedback to position the cart under the pendulum to balance it. And in fact, that balancing can be done even when we modify the system in a variety of ways, as you'll see in this clip. So let's take a look at that, remembering that this is just a brief excerpt from a longer discussion.
[VIDEO PLAYBACK]
I can change the overall system even further by, let's say, for example, pouring a liquid in. And now, let me also comment that I've changed the physics of it a little bit because the liquid can slosh around a little bit. It becomes a little more complicated a system, but as you can see, it still remains balanced.
[END VIDEO PLAYBACK]
As you'll see when we get to it, by the way, that demonstration was a lot of fun to do. Now, in talking about signals and systems as we go through the course, there are several domains, two in particular, that we will find convenient for the analysis and representation of signals and systems. One is the time domain, which is what we tend to think of, and which we have kind of been focusing on in the discussion so far in this lecture. But equally important is what's referred to as the frequency domain as a representation for signals, and as a means for analysis for systems. And in the context of the frequency domain representation, some of the kinds of ideas and topics that we'll be exploring are the Fourier Transform, and the Laplace Transform, and a discrete-time counterpart of the Laplace Transform, which is the z-Transform.
The Fourier Transform discussion we'll get into fairly early in the course. And the Laplace Transform and z-Transform represent extensions of the Fourier transform, and we'll be getting into that later in the course.
Just initially to think about the time domain and frequency domain, you might think, for example, of a note being played. And the time-domain representation would be how the sound pressure, as a function of time, would change. And the frequency-domain representation would correspond to a representation of the frequency content of the note.
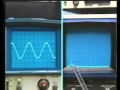
And, in fact, what I'd like to do is illustrate that and those two domains simultaneously by playing a glockenspiel note. What you'll hear is the note repeated several times over. And at the same time, you'll see two displays, one on the left representing the time domain display a representation of the signal, and the one on the right representing the frequency domain.
So let's look at that. And you'll hear the note and simultaneously see these two displays. So there's the note on the left, the time waveform. And on the right, what we see is the frequency content, in particular, indicating the fact that there are several harmonic lines in the tone.
Well, what I've gone through in this lecture represents a brief overview of signals and systems. And beginning with the next lecture, we will be much more specific and precise, first discussing some basic signals, and then talking about systems, and system properties, and how to exploit them. As one final comment that I'd like to make in this lecture, I'd like to emphasize at the outset that the taped lectures represent only one component of the course. And equally important will be both the textbook and the video course manual.
In particular, it's important not only to be viewing the tapes, but simultaneously, or in conjunction with that, doing the appropriate reading in the textbook and also working through the problems carefully in the video course manual. In a course like this, you basically only get out of it as much as you put into it. The hope is that if you put the right amount of time and effort into it, you'll find the course to be educational and interesting. And I certainly hope that that will be the case. Thank you.