Descriptions: Throw a rectangular object with sides of three different lengths (such as a cereal box), into the air. You can get the box to tumble stably about its longest axis, or about its shortest axis. But if you try to make it tumble about it middle axis, you will find the motion is unstable. The model of the angular momentum is a nonlinear system of three differential equations. There are six critical points: the four corresponding to the long and short axes are stable; the two corresponding to the middle axis are unstable.
Related MATLAB code files can be downloaded from MATLAB Central
Instructor: Cleve Moler
PROFESSOR: Here are the differential equations for the angular momentum of a tumbling box. Try throwing a book, or a box, or any rectilinear object whose three dimensions are all different, into the air with a twist, to make a tumble.
You could go to rotate about its longest axis, or about its shortest axis. But you can't get to rotate about its middle axis. Let's examine that phenomena numerically.
Here's the anonymous function defining those system of three first order differential equations. Now I'm going to start with an initial condition that's near the first critical point. 1, 0, 0 is a critical point. And I'm going to take 0.2 times a random number, to sort of be near the critical point, and then normalize it, so that it has length 1.
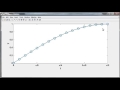
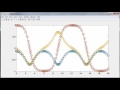
So the largest component is the first component. And the other two are small, but not too small. This is an easy problem numerically. There's no stiffness involved here. So I'm going to use ODE 23, integrate from 0 to 10, and here's the solution.
The blue component is the first one, and it stays near 1. And the other two are periodic, rotating around the 0. Let's go back and take another starting condition. Here it is again.
Now the other two components are really small. And when we integrate that, the blue component stays flat near 1. And the other two guys hardly move at all.
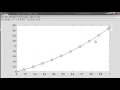
Now I'm going to go to the third critical point, 0, 0, 1. Do the same thing. Take a random number near there. Use ODE 23. Now the yellow component stays near one. And the other two move periodically around 0.
Run that again. The third component is near 1. The other two are not too big. And run the ODE 23. The other component stays near 1. And the other two rotate periodically around 0.
Now we're going to go to the middle critical point. We're going to try and get the box to rotate around its middle axis. The second component is the one near 1. And now we see completely different behavior.
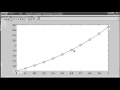
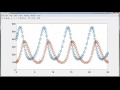
This sienna component doesn't stay near 1. It goes down near -1, and comes back up. Let's integrate over a longer period, so we can see that behavior.
So it's periodic. But it goes down to -1 and comes back to 1. And the other two move in large amplitudes around 0. So this is the instability of that middle critical value.
Let's doing again. Same thing. 1 down to -1, and back up. It's periodic. These solutions are all periodic. But that middle critical point is unstable. Now I want to view these in a different way, graphically.
The differential equations have these three critical points. Any solutions to start exactly in these initial conditions stay there. But what happens if you start near these initial conditions?
Well it turns out, that x and z are stable critical points. But y is an unstable critical point. If the angular momentum is near x or near z, it stays near there. But if it starts near y, it moves away quickly.
You can think of x as the short axis, and z is the long axis. Rotation near the short axis is stable. And rotation near the long axis a stable. But rotation near the middle axis is unstable.
We can see that in the following graphic. It turns out that if a solution starts with an initial condition that has norm 1, it stays with norm 1. So the solution lives on the unit sphere.
Here's our unit share with our three critical points, x, y, and z. If this were the Earth, z will be the North Pole. Axis where the 0-th meridian crosses the equator. That's in the east Atlantic, a little off of West Africa. y would be where the 90th meridian crosses the equator. That's in the Indian Ocean, west of Sumatra.
If we start with an initial condition near x, the solution orbits around x. That's stable rotation around the short axis. If we start with an initial condition near z, the solution orbits around z. That's stable rotation around the long axis.
But if we start near y, the solution takes off, goes over to near -y, turns around, and comes back to y. Periodic, but goes clear around the globe. That turns out, that's a circle actually, an orbit around x.
If we come up a little above y, we get an orbit around z. Go down a little below y, we get an orbit around -z. Go to the right of y, we get an orbit around -x.
Let's zoom in a little bit. And we can see that y is a classic unstable critical point. Let's conclude by drawing a few orbits.