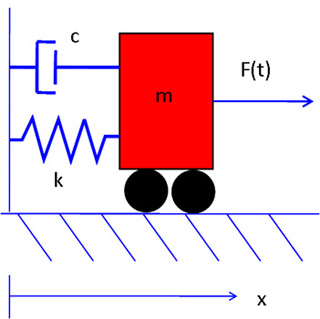
A moving cart attached to a wall by a spring and a dashpot. The equations of motion for every 1-degree-of-freedom system can be linearized around the equilibrium points to the second order differential equation that describes this system. Thus, understanding the free response and selected forced responses for this system can give deep insight into the stability of the equilibrium points and the behavior of a large number of systems. See Lectures 20 and 21 for more information. (Image by MIT OCW.)
Instructor(s)
Prof. Nicholas Hadjiconstantinou
Prof. Peter So
Prof. Sanjay Sarma
Prof. Thomas Peacock
MIT Course Number
2.003J / 1.053J
As Taught In
Spring 2007
Level
Undergraduate
Course Description
Course Features
Course Description
Introduction to the dynamics and vibrations of lumped-parameter models of mechanical systems. Kinematics. Force-momentum formulation for systems of particles and rigid bodies in planar motion. Work-energy concepts. Virtual displacements and virtual work. Lagrange's equations for systems of particles and rigid bodies in planar motion. Linearization of equations of motion. Linear stability analysis of mechanical systems. Free and forced vibration of linear multi-degree of freedom models of mechanical systems; matrix eigenvalue problems. Introduction to numerical methods and MATLAB® to solve dynamics and vibrations problems.
Other Versions
OCW Scholar Version 
Other OCW Versions
These different OCW versions provide complementary materials, including lecture videos, detailed lecture notes, and many sample problems.


