Flash and JavaScript are required for this feature.
Download the video from iTunes U or the Internet Archive.
Topics covered: Battery simulation
Instructor/speaker: James Geraci, Sudarshan Raghunathan, and John Chu
Project: Battery Simulation
The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high quality educational resources for free. To make a donation or view additional materials from hundreds of MIT courses, visit MIT OpenCourseWare at ocw.mit.edu.
JAMES GERACI: My name's James Geraci. I worked with Sudarshan and John Chu on this project. And what we did is we took a numerical simulation, electrochemical simulation, of a battery and ported it to the Playstation 3. So the objective of this project for this situation was to port an electrochemical simulation to the PlayStation 3 and try to take advantage of the unique features of the cell processor to help speed up the computation of the simulation.
So when we talk to everyone, we talk why we'd want to do that. We're going to discuss the model. We're going to discuss how we solved it numerically, look at some of our performance results, and then discuss what we wish we could have implemented.
So the justification is basically the world needs energy, and oil has been in the news a lot and hasn't been as a reliable source of energy as we'd like. So in the automotive industry, hybrids seem to be part of the solution to the energy needs.
Now, one the problems of hybrids is how much energy is in your battery. So the more sophisticated battery model that we can put in a hybrid, the better that we're going to be off. So a more sophisticated model requires more computation, so you're looking at having a large superscalar processor in your car, or you could see if you could get a lot of small processors to do the same amount of work. And the cell represents the first opportunity be able to test that out.
So the simulation that we ran basically consisted of a lead acid battery cell. So unfortunately, they used the word "cell," and we're also using the word "cell." So it's sort of like the modern day Smurf. So in a lead-acid battery cell, you have a lead dioxide electrode, which consists of a number of parts; a lead electrode, which also consists of a number of parts; and an electrolyte, which is 5 molar sulfuric acid, which consists of H2SO4.
When you discharge the battery, you're going to close the circuit. And basically, what ends up happening is you have electrons flying on the outer loop. And between the electrodes, you're going to have an ionic current. So you have a complete circuit around your loop. And this is the effect that the simulation is trying to simulate.
The simulation works on a very low physical level, and it stimulates the chemical reactions, which at the lead dioxide electrode, it converts lead dioxide into lead sulfate during discharge, reverses it during charge. During discharge, the lead electrode turns lead into lead sulfate. And during recharge, it converts that back.
To implement the model, we took basically and discretized the system and just kind of cross-sectioned it-- took small sections and cross-sectioned it. We're going to skip this slide. I don't know what that is. But basically, to simulate the physics, we have a bunch of nasty, nonlinear coupled partial differential equations. This is an example of two of them.
And there are a number of other ones that are included in the system but not really worth seeing. Just kind of a feel, you see a diffusion term. In the lower equation, you see a diffusion term. You see a reaction term. And the upper equation, you see changing of the porosity, changing the geometry of the system.
This is kind of the output that you could get from this type of battery simulation. And what you're looking at here is you're looking at-- if the left-hand side is the electrodes, is the top of the battery, and the height of the battery goes along that way, you see that as you discharge, the concentration at the top of the electrodes is much-- the acid is consumed where you're drawing current out most readily. So physically, the simulation kind of makes sense, even if my speech didn't.
The battery model that we used is a two-dimensional model. It has both a lead dioxide electrode and a lead electrode and an electrolyte area. This is an example of just the lead dioxide electrode. And if we discretize that in two dimensions, we would get a discretization that looks like that if we were to use a single-centered finite-volume method.
But it turns out that we have so many discontinuities in here that it's much better to use a staggered grid. And so we're using actually two different meshes to simulate this system. Well, on a single mesh, you would end up having four corners, four edges and a center. So you would get nine different types of objects and one electrode alone. And you're talking about a rather large and nasty simulation.
On a small scale, the simulation would produce a very sparse matrix that looks something like this. And Sudarshan will now come up and talk to you about the matrices and how we solved this system.
SUDARSHAN RAGHUNATHAN: [INAUDIBLE] slight context [INAUDIBLE] speakers. So basically, like John said, the problem, we are essentially trying to parallelize the most computationally expensive part of this whole simulation, this solving for the Newton iterations during each [? lower ?] step. And so basically, in an abstract-- I'm sorry. Any questions?
AUDIENCE: Speak louder.
SUDARSHAN RAGHUNATHAN: Sorry?
AUDIENCE: Louder.
AUDIENCE: [INAUDIBLE]. The microphone [INAUDIBLE].
SUDARSHAN RAGHUNATHAN: I'll try, but you've got to try and listen harder too.
PROFESSOR: That only works for the TV. You have to yell at them.
SUDARSHAN RAGHUNATHAN: I got it, yeah. Is it any better now?
PROFESSOR: No, you've got to yell at them.
SUDARSHAN RAGHUNATHAN: Is it any better now?
AUDIENCE: Yeah.
SUDARSHAN RAGHUNATHAN: OK, cool.
PROFESSOR: Yeah, I can hear.
SUDARSHAN RAGHUNATHAN: So--
[LAUGHTER]
Yeah, I always like to say I'll try to speak harder. You should try to listen harder, too. So we meet somewhere in between. So basically in an abstract sense, we are trying to solve a system of sparse linear equations. And for simplicity, for the first pass, we treated the matrix as being dense. So we did the whole Gauss elimination ignoring all the zeroes of the matrix.
And so the basic idea is that we do Gauss elimination with partial pivoting. And it's the forward elimination stage of the Gauss elimination that [? Rn cubed ?] that is most expensive. And that is the thing we've tried to parallelize between among the SPUs. And the partial pivoting and the back subs are done on the PPUs because that turned out to be much faster.
So this is the matrix that we are considering during each step for the random entries and for the random right-hand side. And then so the way Gauss elimination works is that we start off with one of the rows that you call the base row, which is where the pivots come from.
And then we eliminate the variable corresponding to base row from all the subsequent elimination rows. And all these eliminations can be done in parallel. And that's what we have tried to parallelize. So each SPU grabs hold of the next available elimination row, eliminates it, and writes a result back on to the main memory.
So if, for example, if we consider the situation with the two SPUs, what we do is that we stream the elimination rows across all the SPUs. Each SPU performs the elimination and writes the result back to main memory, as you can see.
And this happens for every row. So in this simulation, the first variable has been eliminated. As you can see, there are zeroes along the first column. And the process is recursive. After the first variable is completed, it moves on to the next variable.
And the way the elimination rows are returned, they're delivered in a cyclical fashion. So there is no serial bottleneck. It's all perfectly load balanced.
PROFESSOR: Have you--
SUDARSHAN RAGHUNATHAN: I'm sorry?
PROFESSOR: --change?
SUDARSHAN RAGHUNATHAN: I'm sorry?
PROFESSOR: If you eliminate something lower, doesn't the pivot value change? I'm completely not getting what you are saying. That's my first question.
SUDARSHAN RAGHUNATHAN: Yes.
PROFESSOR: Second question is, is this sparse or dense? What's your matrix representation?
SUDARSHAN RAGHUNATHAN: The matrix representation currently is dense.
PROFESSOR: OK.
SUDARSHAN RAGHUNATHAN: Yeah, so we've--
PROFESSOR: Doesn't the pivot value keep changing when you eliminate? So if it's completely parallel, and doesn't that [INAUDIBLE]?
SUDARSHAN RAGHUNATHAN: So all the subsequent variables that are eliminated for each variable, all can be done in parallel. But after one variable has been eliminated, there's a synchronization step where all the SPUs have to synchronize. There's a barrier after each row has been eliminated.
PROFESSOR: OK.
SUDARSHAN RAGHUNATHAN: Yeah, so you start it-- so there's a totally [INAUDIBLE], if you write the algorithm down. And then it's the inner two loops that are totally parallelized with. And the second loop is what we're trying to parallelize.
PROFESSOR: OK.
SUDARSHAN RAGHUNATHAN: Is that a little clearer? Yeah. So this is the basic algorithm. And I'll let John talk about some of the performance numbers we've got. But some of the optimizations that we haven't done are the use of the [? last three ?] operations, like extreme multiple rows at a time and use of [INAUDIBLE] operations. But I'll let John talk about the performance numbers.
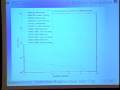
JOHN CHU: Computation of the current elimination row with the fetching of the next elimination row, we get roughly a 30% speedup. So here's a graph to see how both the unbuffered and buffered version perform scattered with a number of SPUs. So as you can see, both look roughly pretty linear. And that makes sense because the--
So here's another graph of how we scaled with the size of the matrix that we're working with. So the smaller the matrix, the higher the communication/computation ratio. So the communication latency should be more apparent. But as you can see, even as you get smaller, the computations is still pretty linear. So--
PROFESSOR: Yeah, it's linear. But it's not just [INAUDIBLE]. It's not running at 2x performance improvement. But [INAUDIBLE] now. So when you put 16 there, why is it only 30%? Why is it not leading to 2x performance improvement? So is it because of underclock? Because if it's underclocked, your graph shouldn't have this kind of a pattern. It should have a more exponential type pattern. [INAUDIBLE].
PROFESSOR: Did you understand the question?
JOHN CHU: Yep.
PROFESSOR: So why aren't you getting a 2x speedup? I mean, your line is straight, but it's not increasing proportional to the number of SPUs you're increasing. So your efficiency might not be at 100%. Any idea why?
JAMES GERACI: Yeah, that [? looks ?] horrible.
JOHN CHU: The 2x is only-- this is [INAUDIBLE] [? laptop ?], so two would only shift it up and down, right?
PROFESSOR: So it looks like you're not operating at 100% efficiency, right?
JAMES GERACI: Oh, definitely not.
JOHN CHU: Yeah.
PROFESSOR: So I think to--
PROFESSOR: [INAUDIBLE] conversation going on there. But this a strange type of a graph because if [INAUDIBLE] as you get a very nice linear [INAUDIBLE]. If you have [? undersize ?] coordinate, what you get is you have a good speed at very beginning, and then you slow down. You get a [INAUDIBLE] type of a graph. So it's very much-- I haven't seen things like a strange line, but not as [INAUDIBLE] on your graph. This is kind of a strange thing. [INAUDIBLE] to see where and why does it happen.
JOHN CHU: OK. Well, yeah, so I'll just move on. So I'll talk about some of the further work we're trying to do.
PROFESSOR: John?
JOHN CHU: Yeah?
PROFESSOR: Can you clip the mic to your-- yeah, that'll work.
JOHN CHU: So we've also tried to triple buffer by pipelining the fetching of the next row with the computation of the current row with the sending of the previous row. We did this, but it didn't actually give us the speedup that we thought we would get.
But what we're working on how is SIMDizing the computation stage. So right now, we treat all the doubles in the rows as scalars. But by SIMDizing, hopefully we can get a speedup by a factor of two.
And also right now, our LU algorithm isn't very smart in that when we fetch the elimination row, as we go on through the algorithm, part of the elimination row becomes zeroes as we move down. So we don't really need to fetch the entire elimination row. And so by taking that into account, our DMA transfers are smaller. And maybe that will help speed up things a bit.
PROFESSOR: So is the whole thing using double precision?
JOHN CHU: Yes. It's in double precision.
AUDIENCE: Do you have any megaflops you're getting?
JAMES GERACI: We have gigaflops. I think we're getting around 2 gigaflops.
JOHN CHU: So here's the gigaflops graph.
AUDIENCE: Do you know what the expected for [INAUDIBLE]?
JAMES GERACI: [INAUDIBLE] algorithm bias, just [INAUDIBLE].
AUDIENCE: This is a linear scalar on the y-axis?
JAMES GERACI: Yeah, it's [INAUDIBLE].
AUDIENCE: Any idea why you have this [INAUDIBLE] at 3 SGUs? Your double buffering result just drops.
JAMES GERACI: Actually, we have no idea. [INAUDIBLE]. I don't know if we consistently checked [INAUDIBLE].
AUDIENCE: You might want to run it a few more times. There is a recent series of papers by Jack Dongarra's group aimed at double-precision computations. They used single precision, did an approximate guess, and then did a few iterations of an iterative approach to get a double-precision result.
JAMES GERACI: Yeah, those don't work very well for [INAUDIBLE]. And this is conditioned around 10 to the 8. So that's kind of out of the ballpark of the [INAUDIBLE].
SUDARSHAN RAGHUNATHAN: And the particle [INAUDIBLE] that they do, they tried to do [INAUDIBLE] computation. And the main reason they do [INAUDIBLE] because they say [INAUDIBLE]. And then in doing this, the hope is to generalize this to sparse matrices later on. And I think they are trying to do some work with sparse matrices, but they haven't gotten there.
AUDIENCE: One additional question. Just at a high level, is this the right way to tackle this particular problem? It strikes me that there must be a closed-form high-level microscopic model for battery self-discharge.
And I don't know anything about the chemistry lead acid batteries, but the little write-up on the website mentions Black-Scholes, which I do know something about. And of course, there are efficient ways of doing that.
JAMES GERACI: Sure, there are efficient ways of doing Black-Scholes. There are different ways of doing this. This is only one of the equations that's similar to Black-Scholes. There are multiple equations that go into this. They're all coupled. They're all nonlinear.
So solving this system of equations is, in the literature, if you were going to choose this as your model, is--
AUDIENCE: But if you were actually in the business of building and operating batteries--
JAMES GERACI: The problem with--
AUDIENCE: --wouldn't you try and come up with an efficient microscopic model rather than--
JAMES GERACI: Well, it depends on what your compute costs are. I mean, if you're going to run a model on a superscalar processor, that' very expensive processor. If, however, now you have the ability to use a collection of small, cheap little processors like this, you can maybe have the luxury of using a much more sophisticated model.
AUDIENCE: Is it necessarily more sophisticated? I mean, is there some fundamental reason why you'd get more information out of this approach than out of a higher level model?
JAMES GERACI: You get a lot more detail as to what's going on within your battery. A higher level model will give you I/O information. But if you're trying to find failure mechanisms, you may want to know how much pressure's going on at certain points in your battery.
Especially with lithium ion batteries, when you-- this differs from a lithium ion battery in that we're actually changing the state, the type of matter that we're using. And in lithium ion battery, we're intercalating and deintercalating. And so what we're doing is we're creating a lot of stress on a matrix, a crystal. And that will be a failure mechanism.
A simple input/output relationship will not give you that failure mechanism. So you may want to know that kind of information. You may want to know heat information also. You could include thermodynamical information to this kind of model.
AUDIENCE: OK, that's a good answer. I take that to mean that the reason for doing this is if your researching the physics of battery discharge as opposed to trying to estimate how much power's left in your battery.
JAMES GERACI: Well, if you have the computation power, you could use the same model that does the research as the car. And so if you-- yeah, if you can use small processors. So our demonstration-- if you guys want to see print def statements. Otherwise--
PROFESSOR: No, I think we're over time.
JAMES GERACI: Yeah.
PROFESSOR: Any last questions?
AUDIENCE: Wait, just so I understand the sparse versus dense issue, if you just do a sparse elimination on a uniprocessor, do you get a bigger speedup?
JAMES GERACI: Oh, you get a much bigger speedup.
AUDIENCE: OK.
JAMES GERACI: The LU is about the slowest thing you could possibly choose, but if it works.
AUDIENCE: OK, but what you have would still usable for dense matrices?
JAMES GERACI: It'd still be useful for dense matrices, yeah.
AUDIENCE: And do you compare it all to just PPU performance on a dense matrix?
JAMES GERACI: No, we didn't compare it to the PPU. We had it compared-- the same model I'm running on a PC.
AUDIENCE: Yeah.
PROFESSOR: OK, thank you, speakers.
[APPLAUSE]