Flash and JavaScript are required for this feature.
Download the video from iTunes U or the Internet Archive.
Topics covered: Backgammon tutor
Instructor/speaker: Eddie Scholtz and Mike Fitzgerald

Project: Backgammon Tutor
Related Resources
(PDF)
The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high quality educational resources for free. To make a donation or view additional materials from hundreds of MIT courses, visit MIT OpenCourseWare at ocw.mit.edu.
EDDIE SCHOLTZ: So, I'm Eddie Scholtz and this is Mike Fitzgerald and we worked on a backgammon tutor. And to start off, let's see a show of hands. Who here knows how to play backgammon? OK, a few. So to give you an idea of how it works, it involves both skill and luck. And it's a two player game. And the object is to move all your pieces past your opponent's pieces and off the board.
So white's trying to move his pieces this way, down and across. And brown's trying to move his pieces the other way. And you move by rolling the dice. Some important rules are that you can not land on a point on which your opponent has two or more pieces. And if your opponent only has a single piece there, you can land on it and send it back to the beginning.
So the goals of this project when we started off were, first of all to implement the rules of backgammon and get the game going, and that took a good amount of work. Next we wanted to create or find the function that evaluates or says how good a given board is. And then we wanted to be able to look into the future, in order to better determine what move to choose now. And this is the part of the program that we parallelized. And finally our last goal was to try to teach the player how to improve by suggesting why one move might be better than another in English.
So to start with, the two basic kinds of board evaluation are just a static evaluator and a neural net. And the static evaluator works by looking at features of the board and creating a score based on that feature, and then multiplying it by weight based on how important that feature is, and summing them up.
So a program like this was created by Hans Berliner at CMU in 1979, and it was actually the first program to beat a ruling world champion. And they said the program got a little lucky but it did win. And one of the important features was it adjusted the weights as the game went on, because certain features became less important as the game progressed and other features became more important.
So the next approach that people have used is framing neural nets to determine how good a board is. And these have been really successful. They work by basically playing hundreds of thousands, if not millions of games against itself. And so it improves this way. And after about a million and half games it reaches its maximum performance.
And one such board evaluator is Pubeval which was released by Gerry Tesauro in 1993. And this is the evaluation function that we used for our program. Looks like we lost network connection. This is the evaluation function that we used for our program. And he sort of released this as a benchmark evaluator so that other people in the development community could have something to compare their evaluators against. And it plays an intermediate level if not a pretty strong level.
So our next goal was to implement the search the looks into the future in order to help choose the best move now. One of the challenges of this is that the branching factor is so large because you don't know what the dice rolls are going to be in the future. And like in checkers, the branching factor is 10. In chess it's 35 to 40. But in backgammon, for a turn it's around 400.
Another challenge that we faced in the search was that the Pubeval function that we used is not zero sum. So that produced some challenges that you'll see. And also there's the question of whether searching deeper actually does produce better play. And most papers say that the board evaluator is more important than searching deeper. But they do say that searching into the future does improve play, and especially when you're already at a pretty high level of play where everyone's near the same and playing really well. A slight increase in performance could make a big difference.
So here's an illustration of the search tree to give you a better idea of how it works. So say it's X's turn. There might be 20 or so moves that he can commit. Now these are a series of moves. So you roll the two dice, and if they're doubles you get four moves. Certain turns you may not be able to move at all so you might not have any moves. So that really varies. So after those 20 moves the other player, O is going to roll. And there's 21 different dice combinations he can have. And then for each of those there's about 20 moves. And then it's X's roll. And once again he has 21 dice combinations. And then X's move. So this is looking two moves into the future.
So the idea is to build this search tree, and then at this point we're already up to 3.5 million boards. So you have all these leaf nodes that represent your boards, and you're going to evaluate them with your evaluation function to determine how good they are. Since it's not zero sum, you have to evaluate it for both player and both of these values need to get passed up as you're going to move back up the tree to determine the best move.
So you start at the bottom and you say that since it's X's move he's going to choose the best possible move given that roll. And then in order to move up further and calculate the value for the parent node, you say it's equal to the probability of the dice roll for the child node times the value that's stored in that child node. And then you keep doing this and repeating this. O picks his best move and sort of sums the expected value. And then get back up the top and X picks his best move.
So now I'm going to hand it over to Mike who's going to talk about the part of the code that we parallelized.
MIKE FITZGERALD: There's a question.
AUDIENCE: Quick question. Can you use alpha beta pruning? You know about alpha beta pruning?
EDDIE SCHOLTZ: Yeah. People have used that and just like a [INAUDIBLE] search of narrowing it down.
AUDIENCE: Typically by down to the square root of n. So you would have a 20 branch effect rather than a 400. It seems like a real payoff if you could make it work here. I don't know if there's some reason on the back end why it's hard.
EDDIE SCHOLTZ: Well, we actually didn't get to that point. We just spent a lot of time just implementing rules of the game.
MIKE FITZGERALD: All right, so the first thing we looked at and said this would be perfect for parallelizing is just the brute force evaluation of those million boards that you get down to at the end. Which if you run through on one processor just takes a while. Generally an evaluation of a board, regardless of its state takes the same amount of time. So we just had to split the number evenly between SPUs. We had to keep it around a multiple of four just to get the DMA calls to line up nicely with the floats that we were returning and things like that.
So if you're evaluating a million boards which was our number for our benchmarks that we did, each SPU has about 170,000 to handle, and it clearly can't take all those over at once. So each SPU knows where it's supposed to start and how many it's supposed to do. And it knows how much it can pull over. So it does a DMA call to pull in as much as it can process. It processes those, evaluates them, returns them, and gets to the next bunch. So that is what we were able to implement.
There's also a good opportunity for double buffering there for pulling them in as it's actually evaluating the previous ones. So that would be actually a pretty easy step to do next. But each of those six are roughly finished at the same time and then get back to the PPU to evaluate, to run up that tree. And another opportunity to make it a bit quicker, which we didn't quite get to would be SIMDizing the evaluation function so we could do four boards at once with vector engines instead of just one.
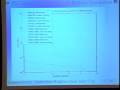
So the performance that we got when looking at the number of SPUs we were using was actually roughly in proportional to the number of SPUs we were using. It's actually 18.18 at the top there. So when using two instead of one we got just about half. When using three instead of one we got just about a third. If you just look at this speedup graph it's pretty much one to one from the number of SPUs we were using to the amount of time it took. So it was a pretty efficient algorithm for splitting those up and evaluating them and pulling them back together.
I'll give you a brief demo. I'll show you quickly how it looks. We might have to fudge our network connection a little bit here. So we used just an [INAUDIBLE] Windows setup to display our [INAUDIBLE] we were using. So I'm just going play a couple rounds of the display, let's say against the computer.
So you can see the computer just took a couple of moves there. But basically what we get here is a print out of a text representation of the board. And then it's my turn. I rolled a six and a two. It does its own evaluation and says this is what the best move combo would be for me at this point.
In the ideal tutoring situation we don't let the user pick what they thought was the best and then tell them why not, but right now, with the time we had this is how we did it. And then it lists all the legal possible moves you can make. Let's say I want to move from 0.6 to 0.4. It moves my piece up there, and from 8 to 2 for example. And the computer makes its couple of moves. That's the general idea.
You can run the computer against itself as many times, just to test different evaluation functions against each other. You can also do it without the animation on the GUI so that it runs a lot quicker. But that's the general idea.
Just to wrap up, four more slides. The way we went about this basically was, we just got sequential code working on just the PPU, got the rules of the game worked out, all the weird conditionals and things that can happen in backgammon and we fixed out our bugs and our memory leaks and things like that. We just shelled out the parallel code and got that working on the PPU, then on one SPU, and then on six.
So it was a pretty clean process of doing it. And we ran into a few walls. We aren't really backgammon experts or even intermediate players, so it was kind of a new thing for us to make sure we had the rules right, and we weren't doing stupid things here and there. But also managing the search tree was a big deal. And looking at what the program has to do in running the game, that's the next thing we want to tackle as far as paralyzing goes. It takes a while, and it's pretty tough. We ran into some memory management issues with how we were representing our boards. We were able to pack them down into, I think 24 byte structure, 20 byte structure to be able to pass more to the SPUs at one time.
PROFESSOR: [INAUDIBLE] What's the general idea for [INAUDIBLE]?
MIKE FITZGERALD: I'm sorry, I missed the beginning of your question because it wasn't on speakerphone.
PROFESSOR: [INAUDIBLE].
EDDIE SCHOLTZ: Are you talking about moving into the future? Are you talking about looking into the future? Yeah. So we built the code for creating that tree and evaluating the leaf nodes. We didn't quite have time to finish up--
PROFESSOR: [INAUDIBLE] I can't hear you through this [INAUDIBLE].
EDDIE SCHOLTZ: OK. We created the code for constructing the tree and evaluating the leaf nodes. We haven't quite has time to finish up moving back up the tree. So at this point we're now looking ahead more than just the moves for now, for like one move.
PROFESSOR: OK. OK.
EDDIE SCHOLTZ: But we got the parallel code working for actually evaluating the boards. It shouldn't be too hard to--
MIKE FITZGERALD: Just extend that tree.
EDDIE SCHOLTZ: To move back up the tree and see what the best move is now.
EDDIE SCHOLTZ: Yeah, so that's basically as far as the road blocks we hit were.
EDDIE SCHOLTZ: Any other questions? Yeah, just some future ideas. One of the big ones is for training, the evaluation functions using neural nets. That takes a lot of time to play hundreds of thousands, millions of games. So one of the ideas is to parallelize that to help speed that up. And I think we're about out of time, so that concludes it. Are there any questions?
AUDIENCE: I'm just curious, you said looking far into the future doesn't necessarily help as much as the evaluation function. Does that mean that AI backgammon is-- I mean how computationally intensive is a good player? I mean, is it a computationally problem? Would you benefit from the parallelism in a practical setting?
MIKE FITZGERALD: Well, just looking at how long it takes to go through those million boards, if you're playing a computer you don't want to wait 18 seconds for them to make their move as opposed to--
AUDIENCE: Oh, so that's time scale of the absolute? If you just ran on a uni-processor for 20 seconds kind of a thing?
MIKE FITZGERALD: Yeah, once you're doing a million boards. And also, if you're on the level of competing against really good competitors, just having a deep search tree to get that much more of an edge would make a difference in that situation. Anyone else? No?
EDDIE SCHOLTZ: Great. Thanks.
[APPLAUSE]