1. Overview and Ionic Currents

• Download English-US transcript (PDF)

MICHALE FEE: OK. So let's go ahead and get started. So what is neural computation? So neuroscience used to be a very descriptive field where you would describe the different kinds of neurons.

Who here has seen the famous pictures-- the old pictures of the golgi-stained neurons, all those different types of neurons, describing what things look like in the brain and what parts of the brain are important for what kinds of behavior based on lesion studies. It used to be extremely descriptive. But things are changing in neuroscience, and have changed dramatically over the past few decades.

Really, neuroscience now is about understanding the brain, how the brain works, how the brain produces behavior. And really trying to develop engineering-level descriptions of brain systems and brain circuits and neurons and ion channels and all the components of neurons that make the brain work.

And so, for example, the level of description that my lab works at and that I'm most excited about is understanding how neural circuits-- how neurons are put together to make neural circuits that implement behaviors, or to produce let's say object recognition. So this is a figure from Jim DiCarlo, who is our department head. Basically a circuit-level description of how the brain goes from a visual stimulus to a recognition of what that object is in the stimulus.

Now at the same time that there's been a big push toward understanding or generating an engineering level descriptions of brains and circuits and components, neurons, there's also been tremendous advances in the technologies that we can use to record neurons. So there are now imaging systems and microscopes that can image thousands of neurons simultaneously.

This is an example of a movie recorded in an awake baby mouse that's basically dreaming. And let me just show you what this looks like. So this is a mouse that has a fluorescent protein that's sensitive to neural activity.

And so when neurons in a part of the brain become active they become fluorescent and light up. And so here's a top surface of the mouse's brain. And you can see this spontaneous activity flickering around as this mouse is just dreaming and thinking about whatever it's thinking about. So one of the key challenges is to take images like this that represent the activity of thousands of neurons or millions of neurons and figure out how to relate that to the circuit models that are being developed.

So here's another example. So there are these new probes where these are basically silicon probes that have thousands of little sensors on them and a computer here that basically reads out the pattern of activity. These are called neuropixels. So those are basically electrodes that can, again, record from thousands of neurons simultaneously. And they're quite long and can record throughout the whole brain, essentially, all at once.

So the key now is you have these very high dimensional data set. How do you relate that to the circuit models that you're developing? And so one of the key challenges in neuroscience is to take very large data sets that look like this that just look like a mess and figure out what's going on underneath of there.

It turns out that people are discovering that while you might be recording from tens of thousands of neurons and it looks really messy that there's some underlying very simple structure underneath of there. But you can't see it when you just look at big collections of neurons like this.

So the challenge here is really to figure out how to not only just make those models, but test them by taking data and relating the patterns of activity that you see in these very high dimensional data sets, do dimensionality reduction-- compress that data down into a simple representation-- and then relate it to those models that you developed.

One of the things we're going to try to do in this class is to apply these techniques of making models of neurons and circuits together with mathematical tools for analyzing data in the context of looking at animal behaviors. So for example, in my lab we study how songbirds sing, how they learn to produce their vocalizations. Songbirds learn by imitating their parents. They listen to their parents.

[BIRDS SINGING]

 

Here, hold on. I'm going to skip ahead. How do I do that?

[BIRDS SINGING]

 

[INAUDIBLE] bring up the-- I was hoping I'd be able to skip ahead.

So this is just a setup showing how we can record from neurons in birds while they're singing and figure out how those circuits work to produce the song. This is a little micro-drive that we built. It's motorized so that we can move these electrodes around independently in the brain and record from neurons without the animal knowing that we're moving the electrodes around and looking for neurons.

So songbirds are really cool. They listen to their parents. They store a memory of what their parents sing. And then they begin babbling. And they practice over and over again until they can learn a good copy of their song.

So here's a bird that's singing with the micro-drive on its head. And you can hear the neuron in the background.

[STATIC SOUNDS]

Sorry, it's not over the loudspeaker here. But can everyone hear that? So we can record from neurons while the bird is singing.

[BIRDS SINGING]

Look at the activity in this network and try to figure out how that network actually works to produce the song. And also we can record in very young birds and figure out how the song is actually learned.

And there's an example of a neuron generating action potentials, which is the basic unit of communication in the brain.

[BIRDS SINGING]

And we try to build circuit models and figure out how that thing actually works to produce and learn this song.

So these computational approaches that I'm talking about are not just important for dissecting brain circuits related to behavior. The same kinds of approaches, the same kind of dimensionality reduction techniques we're going to learn are also useful in molecular genetic studies, like taking transcriptional profiling and doing clustering and looking at the different patterns that are there. It's also useful for molecular studies.

Also, these ideas are very powerful in studying cognition. So if you look at the work that Josh Tenenbaum does and Josh McDermott, who developed mathematical models of how our minds work, how we learn to think about things, those are also very model-based and very quantitative. So the kinds of tools we're going to learn in this class are very broadly applicable.

They're also increasingly important in medicine. So at some point we're going to take a little bit of a detour to look at a particular disease that's caused by a defect in an ion channel. And it turns out you can understand exactly how that defect in that ion channel relates to the phenotype of the disease. And you can do that by creating a mathematical model of how a neuron behaves when it has an ion channel that has this defect in it. So it's very cool. And once you model it, you can really understand why that happens.

So here are some of the course goals. So we're going to start by working on basic biophysics of neurons and networks and other principles underlying brain and cognitive functions. We're going to develop mathematical techniques to analyze those models and to analyze the behavioral data and neural data that you would take to study those brain circuits.

And along the way, we're going to become proficient at using MATLAB to do these things. So how many of you have experience with MATLAB? OK, great.

And not? So anybody who doesn't have experience with MATLAB, we're going to really make an effort to bring you up to speed very quickly. Daniel has actually just created a very nice MATLAB cheat sheet that's just amazing. So there will be lots of help with programming.

So let me just mention some of the topics that we'll be covering. So we'll be talking about equivalent circuit model of neurons. So let me just explain how this is broken down. So these are topics that we'll be covering.

And these are the mathematical tools that go along with those topics that we'll be learning about in parallel. So we'll be studying neuronal biophysics. And we'll be doing some differential equations along the way for that, just first-order linear differential equations, nothing to be scared of.

We'll talk about neuronal responses to stimuli and tuning curves. And along the way, we'll be learning about spike sorting and peristimulus, time histograms, and ways of analyzing firing patterns. We talked about neural coding and receptive fields. And we'll learn about correlation and convolution for that topic.

We'll talk about feed forward networks and perceptrons. And then we're going to start bringing a lot of linear algebra, which is really fun. It's really powerful. And that linear algebra sets the stage for then doing dimensionality, reduction on data, and principal component analysis, and singular value decomposition, and other things.

We'll then take an additional extension of neural networks from feed forward networks. We'll figure out how to make them talk back to themselves so they can start doing things like remember things and make decisions. And that involves more linear algebra, eigenvalues. And then I'm not sure we're going to get time to sensory integration and Bayes' rule.

So by the end of the class, there are some important skills that you'll have. You'll be able to think about a neuron very clearly and how its components work together to give that neuron its properties. And how neurons themselves can connect together to give a neural circuit its properties.

You'll be able to write MATLAB programs that simulate those models. You'll be able to analyze data using MATLAB. You'll be able to visualize high dimensional data sets.

And one of my goals in this class is that you guys should be able to go into any lab in the department and do cool things that even the graduate students may not know how to do. And so you can do really great stuff as a UROP.

So one of the most important things about this class is problem sets because that's where you're going to get the hands-on experience to do that data analysis and write programs and analyze the data. Please install that. It's really important, if you don't already have that.

We use live scripts for problems set submissions. And Daniel made some nice examples on Stellar. And of course the guidelines for Pset submissions are also on Stellar.

OK, that's it. Any questions about that? No? All right, good.

So let's go ahead and get started then with the first topic. OK. So the first thing we're going to do is we're going to build a model of a neuron. This model is very particular. It uses electrical components to describe the neuron.

Now that may not be surprising since a neuron is basically an electrical device. It has components that are sensitive to voltages, that generate currents, that control currents. And so we're going to build our model using electrical circuit components.

And one of the nice things about doing that is that every electrical circuit component, like a resistor or a capacitor, has a very well-defined mathematical relation between the current and the voltage, the current that flows through that device and the voltage across the terminals of that device. So you can write down very precisely, mathematically, what each of those components does.

So then you can then take all those components and construct a set of equations or in general a set of differential equations that allows you to basically evolve that circuit over time and plot, let's say, the voltage on the inside of the cell as a function of time. And you can see that that model neuron can actually very precisely replicate many of the properties of neurons.

Now neurons are actually really complicated. And this is the real reason why we need to write down a model. So there are many different kinds of neurons. Each type of neuron has a different pattern of genes that are expressed. So this is a cluster diagram of neuron type based on a transcriptional profiling of the RNA that I think it was about 13,000 neurons that were extracted from a part of the brain.

You do a transcriptional profiling. It gives you a map of all the different genes are expressed in each neuron. And then you can cluster them and you can see that this particular part of the brain, which is in the hypothalamus, expresses all of these different cell types.

Now what are those different genes? Many of those different genes are actually different ion channels. And there are hundreds of different kinds of ion channels that control the flow of current across the membrane of the neuron. So this is just a diagram showing different potassium ion channels, different calcium ion channels. You can see they have families and different subtypes.

And all of those different ion channels have different timescales on which the current varies as a function of voltage change. They have different voltage ranges that they're sensitive to. They have different inactivation. So many ion channels, when you turn them on, they stay on.

But other ion channels, they turn on and then they slowly decay away. The current slowly decays away. And that's called inactivation.

And all these different ion channels have different combinations of those properties. And it's really hard to predict when you think about how this neuron will behave with a different kind of ion channel here. It's super hard to just look at the properties of an ion channel and just see how that's going to work in a neuron because you have all these different parts that are working together.

And so it's really important to be able to write down a mathematical model. If you have a neuron that has a different kind of ion channel, you can actually predict how the neuron's going to behave. Now that's just the ion channel components. Neurons also have complex morphologies.

This is a Purkinje cell in the cerebellum. They have these very densely elaborated dendrites. Other neurons have very long dendrites with just a few branches. Other neurons have very short stubby dendrites.

And each of those different morphological patterns also affects how a neuron responds to its inputs, because now a neuron can have inputs out here at the end of the dendrite or up close to the soma. And all of those, the spatial structure, also affects how a neuron responds. And those produce very different firing patterns. So some neurons, if you put in a constant current, they just fire regularly up.

So it turns out we can really understand why all these different things happen if we build a model like this. So let me just point out a couple of other interesting things about this model. Different parts of this circuit actually do cool different things. So neurons have not just one power supply. They've got multiple power supplies to power up different parts of the circuit that do different things.

Neurons have capacitances that allow a neuron to accumulate over time, act as an integrator. If you combine a capacitor with a resistor, that circuit now looks like a filter. It smooths its past inputs over time. And these two components here, this sodium current and this potassium current, make a spike generator that generates an action potential that then talks to other neurons.

And you put that whole thing together, and that thing can act like an oscillator. It can act like a coincidence detector. It can do all kinds of different cool things. And all that stuff is understandable if you just write down a simple model like this. Any questions?

So what we're going to do is we're going to just start describing this network. We're going to build it up one piece at a time. And we're going to start with a capacitance.

But before we get to the capacitor, we need to do one more thing. We need to do one thing first, which is figure out what the wires are in the brain. For an electrical circuit, you need to have wires.

So what are the wires in the brain? What do wires do in a circuit? They carry current. So what are the wires in a neuron?

AUDIENCE: Axons?

MICHALE FEE: What's that?

AUDIENCE: Axons?

MICHALE FEE: Axons. So axons carry information. They carry a spike that travels down the axon and goes to other neurons. But there is even a simpler answer than that. Yes?

AUDIENCE: Ion channels?

MICHALE FEE: Ion channels are these resistors here. But what is it that connects all those components to each other?

AUDIENCE: Intracellular and extracellular.

MICHALE FEE: Excellent. It's the intracellular and extracellular solution. And so what we're going to do today is to understand how the intracellular and extracellular solution acts as a wire in our neuron.

And it's not quite as simple as a piece of metal. It's a bit more complicated. There are different ways you can get current flow in intracellular and extracellular solution. So we're going to go through that and we're going to analyze that in some detail.

So in the brain, the wires are the intracellular and extracellular salt solutions. And you get current flow that results from the movement of ions in that aqueous solution. So the solution consists of ions. Like in the extracellular, it's mostly sodium ions and chloride ions that are dissolved in water.

Water is a polar solvent. That means that the negative parts, the oxygen that's slightly negatively charged. Oxygen is attracted toward positive ions.

And the intracellular and extracellular space are filled with salt solution at a concentration of about 100 millimolar. And that corresponds to having one of these ions about every 25 angstroms apart.

So at those concentrations, there are a lot of ions floating around. And those ions can move under different conditions to produce currents.

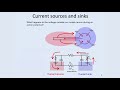
So currents flow in the brain through two primary different mechanisms. Diffusion, which is caused by variations in the concentration. And drifts of particles in an electric field.

So when you put an electric field, so if you take a beaker filled with salt solution, you put two metal electrodes in it, you produce an electric field that causes these ions to drift in-- and that's another source of current that we're going to look at today. So here are our learning objectives for today. We're going to understand how the timescales of diffusion relate to the length scales.

That's a really interesting story. That's very important. We're going to understand how concentration gradients lead to currents. That's known as Fick's First Law.

And we're going to understand how charges drift in an electric field in a way that leads to current, and the mathematical relation that describes voltage differences. And this is called Ohm's Law in the brain. And we're going to learn about the concept of resistivity.

So the first thing we need to talk about, if we're going to talk about diffusion, is thermal energy. So every particle in the world is being jostled by other particles that are crashing into it. And at thermal equilibrium, every degree of freedom, every way that a particle can move, either forward and backward, left and right, up and down, or rotations, this way or this way, or whichever way, I didn't show yet, come to equilibrium at a particular energy that's proportional to temperature.

In other words, if a particle is moving in this direction in equilibrium, it will have a kinetic energy in that direction that's proportional to the temperature. And that temperature is in units of kelvin relative to absolute zero. And the proportionality constant is the Boltzmann constant, which has units of joules per kelvin.

So when you multiply the Boltzmann constant k times temperature, what you find is that every degree of freedom will come to equilibrium at 4 times 10 to the minus 21 joules, which is an amount of energy, at room temperature. At zero temperature, you can see that every degree of freedom has zero energy.

And so nothing is moving. Nothing's rotating, nothing's moving any direction. Everything's perfectly still.

So let's calculate how fast particles move at thermal equilibrium in room temperature. So you may remember from your first physics class that the kinetic energy of a particle is proportional to the velocity squared, 1/2 mv squared. So the average velocity squared of a particle at thermal equilibrium is just 1/2 times that much energy. That makes sense?

Now we [AUDIO OUT] how fast a particle is moving-- for example, a sodium ion. So you can see that the average velocity squared is just kT over m. We just divide both sides by m. So the average velocity squared is kT over m. The mass of a sodium ion is this.

So the average velocity squared is 10 to the 5 meter squared per second squared. Just take the square root that, and you get the average velocity is 320 meters per second. So that means that the air molecules, which have a similar mass to sodium ion, are whizzing around at 300 meters per second. So that would cross this room in a few hundredths of a second.

But of course, that's not what happens. Particles don't just go whizzing along at 300 meters per second. What happens to them?

AUDIENCE: Bump into each other.

MICHALE FEE: Into each other. They're all crashing into each other constantly. So in solution, a particle collides with a water molecule every about 10 to the 13 times per second. 10 to the minus 13 seconds between collisions. So that means the particle is moving a little bit crashing, moving in a different direction, crashing, moving in a different direction and crashing.

So if you follow one particle, it's just jumping around, it's diffusing. So what does that look like? Daniel made a little video that shows to scale. This is position in micron. And time is in real-time.

So this video shows in real-time what the motion of a particle might look like. In each point, it's moving, colliding, and moving off in some random direction. You can actually see this. If you look at a very small particle-- who was it, Daniel, who did that experiment looking at pollen? It's Brownian, at Brown.

AUDIENCE: Yup.

MICHALE FEE: What was his first name? Brown. Brownian motion. Have you heard of Brownian motion? So somebody named Brown was looking at pollen particles in water and noticing that they jump around, just like this. And he hypothesized that they were being jostled around by the water. Any questions?

So what can we say about this? There's something really interesting about diffusion that's very non-intuitive at first. Diffusion has some really strange aspect to it. That a distance that a particle can diffuse depends very much on the time that you allow. And it's not just a simple relation.

So let's just look at this. So let's ask how much time does it take for an ion to diffuse a short distance, like across the soma of a neuron. So an ion can diffuse across the soma of a neuron in about a 20th of a second.

How about down it at dendrites. So let's start our ion in the cell body. And ask, how long does it take an iron to reach the end of a dendrite that can be about a millimeter away. Can take about 10 minutes on average. That's how long it will take an iron to get that far away from its starting point.

So you can see, 20th of a second here. And here it's like 500 seconds. About 10 minutes.

How long does it take an ion, starting at the cell body, to diffuse all the way down-- so you know there are neurons in your body that start in your spinal cord and go all the way down to your feet. So motor neurons in your spinal cord can have very long axons.

So how long does it take an ion to get from the soma all the way down to the end of an axon, a long axon? Somebody just take a guess. It's 20th of a second here, 10 minutes here. Anybody want to guess?

An hour, yup. 10 years. OK. Why is that? That's crazy, right? How is that possible? And that's an ion.

So a cell body is making proteins and all kinds of stuff that have to get down to build synapses at the other end of that axon. And proteins diffuse a heck of a lot slower than ions do. So basically a cell body could make stuff for the axon, and it would never get there in your entire lifetime.

And that's why cells have to actually make little trains. They literally make little trains. They package up stuff and put it on the train and it just marches down the axon until it gets to the end. And this is the reason why.

So what we're going to do is I'm going to just walk you through a very simple derivation of why this is true and how to think about this. So here's what we're going to do. So normally things diffuse in three dimensions, right? But it's just much harder to analyze things in three dimensions..

So you can get basically the right answer just by analyzing how things diffuse in one dimension. So Daniel made this little video to show you what this looks like. This is I think 100 particles all lined up near zero.

And we're going to turn on the video. We're going to let them all start diffusing at one moment. So you can just watch what happens to all these different particles.

So you can see that some particles end up over here on the left. Other particles end up over here on the right. You can see that the distribution of particles spreads out.

And so we're going to figure out why that is, why that happens. So the first thing I just want to tell you is that the distribution of particles, if they all start at zero, and they diffuse in 1D away from zero, the distribution that you get is Gaussian.

And the basic reason is that, let's start at the center, and on every time step they have a probability of 1/2 of going to the right and 1/2 of going to the left. And so basically there are many more combinations of ways a particle can do some lefts and do some rights and end up back where it started.

It's very unlikely that the particle will do a whole bunch of going right all in a row. And so that's why the density and the distribution is very low down here. And so you end up with something that's just a Gaussian distribution.

So let's analyze this in a little more detail. So we're going to just make a very simple model of particles stepping to the right or to the left. We're going to consider a particle that is moving left or right at a fixed velocity vx for some time tau before a collision. And we're going to imagine that each time the particle collides it resets its velocity randomly, either to the left or to the right.

So on every time step, half the particles will step right by a distance delta, which is the velocity times the time tau. And the other half of the particles will step left by that same distance. So they're going either to the left or to the right by a distance delta.

So if we start with n particles and all of them start at position 0 at time 0, then we can write down the position of every particle at time step n, the i-th particle at time step n. And we're going to assume that each particle is independent, each doing their own thing, ignoring each other.

So now you can see that you can write down the position of the particle at time step n is just the position of the particle at the previous time step, plus or minus this little delta. Any questions about that?

So please, if you ever just haven't followed one step that I do, just let me know. I'm happy to explain it again. I often am watching somebody explaining something really simple, and my brain is just in some funny state and I just don't get it. So it's totally fine if you want me to explain something again. You don't have to be embarrassed because happens to me all the time.

So now what we can do is use this expression, compute how that distribution evolves over time, how that distribution of particles, this i-th particle over time, time step n. All right, so let's calculate what the average position of the ensemble is. So these brackets mean average. So the bracket with an i, that I'm averaging this quantity over i particles.

And so it's just the sum of positions for every particle, divided by the number of particles. That's the average position. So again, the position of the i-th particle at time step n is just the position of that particle at the previous time step, plus or minus delta. We just plug that into there, into there.

And now we calculate the sum. But we have two terms. We have this term and that term. Let's break them up into two separate sums.

So this is equal to the sum over the previous positions, plus the sum over how much the change was from one time step to the next. Does that makes sense?

But what is this sum? We're summing over all the particles, how much they changed from the previous time step to this time step. Well, half of them moved to the right and half of them the left. So that sum is just zero.

So you can see that the average position of the particles at this time step is just equal to the average position of the particles at the previous time step. And what that means is that the center of the distribution hasn't changed. If you start all the particles at zero, they diffuse around. The average position is still zero. Yes?

AUDIENCE: [INAUDIBLE] bracket [INAUDIBLE].

MICHALE FEE: Yes. So this here is just this. So this bracket means I'm averaging over this quantity i. So you can see that's what I'm doing here. I'm summing over i and dividing by the number of particles.

AUDIENCE: And what is i?

MICHALE FEE: I is the particle number. So if we have 10 particles, i goes from 1 to 10. Thank you.

So that's a little boring. But we used a trick here that we're going to use now to actually calculate the interesting thing, which is on average how far do the particles get from where they started. So what we're going to do is not calculate the average position of all the particles. We're going to calculate the average absolute value from where they started. Does that makes sense?

We're going to ask, on average, how far did they get from where they started, which was zero. So absolute values, nobody likes. They're hard to deal with. But this is exactly the same as calculating the square root of the average square. It's the same as calculating the variance. Does that makes sense?

So what we're going to do is we're going to calculate the variance of that distribution. And the square root of that variance is just the standard deviation, which is just how wide it is, which is just how far on average the particles got from where they started. Does that makes sense? So let's push on.

We're going to calculate the average square distance. Now we're just going to take the square of that at the end. So the average of the position squared, we're going to plug this into here. So we're going to square it. So the position of the particle squared is just this quantity squared.

Let's factor it out. So we have this term squared plus twice that times that here, plus that term squared. And we're going to now plug that average. So the average position squared is just the average. The average position squared at this time step n is the average position squared at the previous time step plus some other stuff.

And let's take a look at what that other stuff is. What is this? This is plus or minus 2 times delta, which is the step it takes, the size of the step times x.

So what is that average? Half of these are positive and half of these are negative. So the average is zero.

And quantity is the average of delta squared. Well, delta squared is always positive, right? So what does this say? What this says is that the variance at this time step is just the variance at a previous time step is a constant.

So let's analyze that. What this says is that at each time step, the variance grows by some constant. Delta is a distance. Delta squared is just the units of variance of a distribution that's a function of distance.

So if the variance at time step 0 is 0, that means they're all lined up at the origin. One time step later, the variance will be delta squared. The next time step, it will be two delta squared. The next time step, dot, dot, dot. Up at some time step n, it will be n times delta squared.

So you see what's happening? The variance of this distribution is growing linearly. We can change from time steps to continuous time. So the step number is just time divided by tau, which is some interval in time like the interval between collisions.

And so you can see that the variance is just growing linearly in time where the variance is just 2 times d times T, where d is what we call the diffusion coefficient. It's just length squared divided by time. Why is that? Because as time grows, the variance grows linearly.

So if we want to take time, multiply it by something that gives us variance, it has to be variance per unit time. And variance, for something that's a distribution of position, has to have position squared. Yes?

AUDIENCE: But do we like [INAUDIBLE], like that?

MICHALE FEE: It's built into the definition of the diffusion constant, OK? Any questions about that?

And now here here's the answer. So the variance is growing linearly in time. What that means is that the standard deviation, the average distance from the starting point, is growing as the square root of time. And that's key. That I want you to remember. The distance that a particle diffuses from its starting point on average grows is the square root of time.

So for a small molecule, a typical small molecule, the diffusion constant is 10 to the minus 5 centimeters squared per second. And so now we can just plug in some distances in times and see how long it takes this particle to diffuse some distance.

So let's do that. Let's plug in a length of 10 microns. That was our soma, our cell body. It's 10 to the minus 3 centimeters.

Time is that squared, length squared. So it's 10 to the minus 6 centimeters squared divided by the diffusion constant. 2 times the diffusion constant, 2 times 10 to the minus 5 centimeters squared per second. You can see centimeter squareds cancel. That leaves us time. 50 milliseconds.

Now let's put in one millimeter. That was the length of our dendrite. So that's 10 to the minus 1 centimeter.

So we plug that into our equation for time. Time is just L squared-- I forgot to actually write that down. Here's the equation that I'm solving.

So what this equation at the bottom here is saying is some distance is equal to the square root of 2dT. And I'm just saying L squared is equal to 2 dT. And I'm solving for T, L squared over 2d. That's the equation I'm solving. I'm giving you a length and I'm calculating how long it takes.

So if you put in 10 to the minus 1 here, you get 10 to the minus 2 divided by 2 times 10 to the minus 500 seconds, which is about 10 minutes.

And now if you ask how long does it take to go a meter, that's 10 to the 2 centimeters. That's 10 to the 4 divided by 10 to the minus 5. Somebody over here figured it out right away. About 5 times 10 to the 8 seconds, which is about 10 years.

A year is pi times 10 to the 7 seconds, by the way. Plus or minus a few percent. Any questions about that?

Cool, right? So neurons and cells and biology has to go to extraordinary lengths to overcome this craziness of diffusion, which explains a lot of the structure you see in cells.

So you can see that diffusion causes the movement of ions from places where they're concentrated to places where there aren't so many ions. So let's take a little bit slightly more detail look at that idea. So what I'm going to tell you about now is called Fick's First Law.

And the idea is that diffusion produces a net flow of particles from regions of high concentration to regions of lower concentration. And the flux of particles is proportional to the concentration gradient.

Now this is just really obvious, right? If you have a box, and on the left side of the box you have n particles. Then on the right side of the box then you're going to have particles diffusing from here to there. And you're going to have particles diffusing from there to there.

But because there are more of them over here, they're just going to be more particles going this way than there are that way. Does that makes sense? Let's say each particle here might have a 50% chance of diffusing here or staying here or diffusing somewhere else. Particles here also equally have probability of going either way.

But just because there are more of them here, there's going to be more particles going that way. You can just calculate the number of particles going this way minus the number of particles going that way. And that gives you the net number of particles going to the right.

But what does that look like? You have the number here minus the number some distance away. And what if you were to divide that by the distance? What would that look like?

Good. It looks like a derivative. So if you calculate the flux, it's minus the diffusion constant times 1 over delta, the separation between these boxes. It's the concentration here minus the concentration there. And that is just a derivative. And that's Fick's First Law.

I have a few slides at the end of the lecture that do this derivation more completely. So please take a look at that if you have time.

So now this is really an important concept. This Fick's First Law, the fact that concentration gradients produce a flow of ions, of particles, is so fundamental to how neurons work. And here we're going to be building that up over the course of the next couple lectures.

So imagine that you have a cell that has a lot of potassium ions inside and very few potassium ions outside. Now you can see that you're going to have potassium ions diffusing from here. Sorry, and I forgot to say, let's say that your cell has a hole in it.

So you're going to have potassium ions diffusing from inside to outside through the hole. You also have some potassium ions out here. And some of those might diffuse in. But there are just so many more potassium ions inside than outside concentration-wise that the probability of one going out through the hole is just much higher than the probability of a potassium ion going back into the cell.

So here I'm just zooming in on that channel, on that pore through the membrane. Lots of potassium ions here. On average, there's going to be a net flow of potassium out through that hole.

And we can plot the concentration gradient through the hole. And you can see it's high here, it decreases, and it's low outside. And so there's a net flow that's proportional to the steepness of concentration profile.

So that's true, you get a net flow, even if each particle is diffusing independently. They don't know anything about each other. And yet that concentration gradient produces a current.

All concentration gradients go away. Why is that? Because calcium ions will flow from the inside of the cell to the outside of the cell until they're the same concentration.

And then you'll have just as many flowing back inside as you have flowing outside. Why? So eventually that would happen to all of our cells. Why doesn't that happen?

AUDIENCE: [INAUDIBLE] because they're alive.

MICHALE FEE: Well, that's exactly the right answer, but there are a few intermediate steps. If you were to not be alive anymore, the potassium ions would just diffuse out. And that would be the end.

But what happens is there are other proteins in the membrane that take those potassium ions from here and pump them back inside and maintain the concentration gradient. But that costs energy. Those proteins use ATP. And that ATP comes from eating. But eventually all concentration gradients go away.

So that is how we get current flow from concentration gradients. Now the next topic has to do with the diffusion of ions in the presence of voltage differences, in the presence of voltage gradients.

The bottom line here that I want you to know, that I want you to understand, is that current flow in neurons obeys Ohm's Law. Now what does that mean?

Let's imagine that we have a resistor. Let's say across a membrane or in the intracellular or extracellular space of a neuron. The current flow through that resistive medium is proportional to the voltage difference. So that's Ohm's Law.

The current is proportional to the voltage difference across the two terminals, the two sides of the resistor. And the proportionality constant is 1 over the resistance.

So here current has units of amperes. The voltage difference is units of volts. And the resistance has units of ohms. Any questions about that?

So let's go through-- let's develop this idea a little bit more and understand why it is that a voltage difference produces a current that's proportional to voltage. So let's go back to our little [AUDIO OUT] filled with salt solution. There are ions in here dissolved in the water.

We have two metal plates. We've put a battery between the two metal plates that holds those two plates at some fixed voltage difference delta v. And we're going to ask what happens.

So let's zoom in here. There is one plate that's at one potential. There's another plate at another potential. There's some voltage difference between those that's delta v. The two plates are separated by a distance L.

And that voltage difference produces an electric field that points from the high voltage region to the low voltage region. So an electric field produces a force on a charge-- we have lots of charges in here-- that's proportional to the charge and the electric field.

So what is that force going to do? That force is just going to drag that particle through the liquid, through the water. So why is it?

So if this were a vacuum in here and we put a charge there and metal plates and we put a battery across, what would that particle do? It would move. But what would this force do to that particle?

AUDIENCE: [INTERPOSING VOICES]

MICHALE FEE: Exactly. So what would the velocity do?

AUDIENCE: Increase.

MICHALE FEE: It would just increase linearly. So the particle would start moving. And it would start moving slowly and it'd go-- poof-- crash into the plate. But that's not what happens here. Why is that?

AUDIENCE: [INAUDIBLE]

MICHALE FEE: Because there's stuff in the way. And so it accelerates, and it gets hit by a water molecule. And it gets pushed off in some direction. And then it accelerates in this direction, gets hit again.

But it's constantly being accelerated in one direction before it collides. And so here's what happens. So it's diffusing around. But on each step, it has a little bit of acceleration in this direction, in the direction of the electric field.

And so you can show using the same kind of analysis that we used in calculating the distribution, the change in mean and variance, you can show that mean of a distribution of particles that starts at zero shifts-- of positive particles shifts in the electric field linearly in time.

And you can just think about that as the electric field reaches in, grabs that charged particle, and pulls it in this direction against viscous drag. So now a force produces a constant velocity, not acceleration. And that velocity is called the drift velocity.

So the force is proportional to drift velocity. What is that little f there? Anybody know what that is?

AUDIENCE: Frictional coefficient.

MICHALE FEE: It's the coefficient of friction of that particle. And Einstein cleverly noticed that the coefficient of friction of a particle being dragged through a liquid is related to what? Any guess? Diffusion coefficient of that particle.

Is that cool? That just gives me chills. The frictional coefficient is just kT over the diffusion constant. So if you actually just go through that same analysis of calculating the mean of the distribution, what you find is that v moves linearly in time.

But it's also very intuitive. If you're in a swimming pool, you put your hand in the water, and you push your hand with a constant force. What happens?

Well, let me flip it around. You move your hand through the water at a constant velocity. What is the force feel like? The force is constant, right?

So flip it the other way around. If the force is constant, then you're going to get a constant velocity. Yes?

AUDIENCE: So side question, but you can also look at that like a terminal velocity problem?

MICHALE FEE: Exactly. It's exactly the same thing.

So the drift velocity is proportional to the force by proportionality constant, 1 over the coefficient of friction, which is now d over kT. And what is this force proportional to? Anybody remember? The force was proportional to the electric field.

And so let's calculate the current. So I'm going to argue that the current is proportional to the drift velocity times the area. Now why is that?

So if I have an electric field, it makes these particles, all the particles in this area here drift at a constant velocity in this direction. So there is a certain amount of current that's flowing in this area right here. Does that makes sense?

Now if my electrodes are big and I also have electric field up here, then that electric field is causing current to flow up here too. And if there's electric field up here, then there will be current flowing up here too.

And so you can see that the amount of current that's flowing between the electrodes is proportional to the drift velocity and the cross-sectional area between the two electrodes. Yes? So that's really important.

Now we figured out that the drift velocity is proportional to the electric field. So the current is proportional to the electric field times the area. And the electric field is just the voltage difference divided by the spacing between the electrodes.

And so the current is proportional to voltage times area divided by length. So we have a proportionality. Current is proportional to voltage times area divided by length. And now let's plug in what that proportionality constant is.

This is now like Ohm's Law, right? We're saying the current is proportional to voltage difference. The thing that the proportionality constant here is something called resistivity. Otherwise known as conductivity. But we're going to use resistivity.

So this is just Ohm's Law. It says current is proportional to voltage difference. Let's rewrite that a little bit so that it looks more like Ohm's Law. Current is proportional to voltage difference.

And that thing, that thingy right there, should have units of what? 1 over ohms. Right? So that is 1 over resistance. Let's just write down what the resistance is. Resistance is just resistivity times length divided by area.

So let's just stop and take a breath and think about why this makes sense. Resistance is how much resistance there is to flow at a given voltage, right? So what happens if we make ours really small? What happens to the resistance?

AUDIENCE: [INAUDIBLE] really big.

MICHALE FEE: The resistance gets big. The amount of current gets small because there's less area that the electric field is in. And so the current goes down. That means the resistance is big. If we make our plates really big, the resistance gets smaller.

What happens if we pull our plates further apart? What happens to the resistance?

AUDIENCE: [INAUDIBLE] further apart.

MICHALE FEE: Good. If the plates are further apart, L is bigger, and resistance is bigger. But conceptually, what's going on? Physically, what's going? The plates are further apart, so what happens?

AUDIENCE: [INAUDIBLE]

MICHALE FEE: Right. The voltage difference is the same, but the distance is bigger. And so the electric field, which is voltage per distance, is smaller.

And that smaller electric field produces a drift velocity. And that's why the resistance goes up. Cool, right?

OK. Now, let's talk for a minute about resistivity. So resistivity in the brain is really, really lousy. The wires of the brain are just awful.

So if you look at the resistivity for copper, which is which is the wire that's used in electronics, the resistivity is 1.6 microohms times centimeters. What that means is if I took a block of copper, a centimeter on a side, and I put electrodes on the side of it, and I measured the resistance, it would be 1.6 microohms. That means I could run an amp, that thing with 1.6 microvolts.

Now the resistivity of the brain is 60 ohms centimeters. That means a centimeter of block of saline solution, intracellular or extracellular solution, has a resistance of 60 ohms instead of 1.6 microohms. It's more than a million times worse.

And what that means is that when you try to send current through brain, you try to send some current, the voltage just drops. You need huge voltage drops to produce tiny currents.

That's why the brain has invented things-- axons-- because the wires are so bad that you can't send a signal from one part of the brain to another part of the brain through the wire. You have to invent this special gimmick called an action potential to send a signal more than a few microns away. It's pretty cool, right?

That's why it's so interesting to understand the basic physics of something, the basic mechanisms by which something works because most of what you see is a hack to compensate for weird physics, right? Yes?

AUDIENCE: Does this [INAUDIBLE]?

MICHALE FEE: This high resistivity-- you're asking what causes that high resistivity. It basically has to do with things like the mean-free path of the particle.

So in a metal, particles can go further effectively before they collide. So the resistivity is lower.

AUDIENCE: Is that slope [INAUDIBLE]?

MICHALE FEE: It's a little bit different inside the cell because there's more gunk inside of a cell than there is outside of a cell. And so the resistivity is a little bit worse. It's 2,000 ohms centimeters, or 1,000 or 2,000 inside the cell and more like 60 outside.

AUDIENCE: [INAUDIBLE]

MICHALE FEE: Yes once you're outside the cell, it's basically the same everywhere. OK? So that's it.

So here's what we learned about today. We understood the relation between the timescale of diffusion and length scales. And we learned that the distance that a particle can diffuse grows only as the square root of time.

We understood how concentration gradients lead to currents. And we talked about Fick's First Law that says that concentration differences lead to particle flux. The flux is proportional to the gradient or the derivative of the concentration.

And we also talked about how the drift of charged particles in an electric field leads to currents, and how the voltage current relation obeys Ohm's Law. And we also talked about the concept of resistivity and how the resistivity in the brain is really high and makes the wires in the brain really bad.

So that's all I have. I will take any questions. Yes, Daniel?

AUDIENCE: I just wanted to introduce David.

MICHALE FEE: OK. Our other TA is here. Any questions? Great. So we will see you-- when is the first [AUDIO OUT]? Is that--

AUDIENCE: Tomorrow.

MICHALE FEE: Tomorrow. So I will see you Thursday.