3. Nernst Potential and Integrate and Fire Models

• Download English-US transcript (PDF)

MICHALE FEE: Good morning, everybody. So we're going to continue today developing our model of a neuron. Again, this is called the "Equivalent Circuit Model," and it was developed by Alan Hodgkin and Andrew Huxley in the '40s and '50s.

Let me just give a brief recap of what we've covered in the last couple of lectures. So we've been analyzing a neuron. We've been imagining an experiment in which we have a neuron in a dish filled with extracellular solution, which is a salt solution.

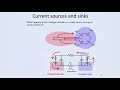
We have an electrode in the cell that's measuring the voltage difference between the inside and the outside of the cell. So we have the electrode connected to an amplifier, a differential amplifier, and a wire in the bath connected to the other side of the differential amplifier. And we have a current source, which injects current into the cell. And we imagine that, as the experimenter, we have our hand on a knob that we can adjust the amount of current that's being injected into the cell.

We've described the neuron basically as a capacitor, because it has a-- it's two conductors separated by an insulator. So we have a conductor, one conductor inside the cell, which is that conductive intracellular salt solution, and another conductor outside the cell, which is the conductive extracellular solution. And those two conductors are separated by an insulator, which is a phospholipid bilayer.

We wrote down the equivalent circuit for this, which for this situation right here it has a voltage measuring device that represents the membrane potential as the difference between the intracellular voltage and the extracellular voltage. We have a current source here, and we've represented our neuron so far as a capacitor. We then introduce the idea of ion channels, or conductances, or pores in the membrane that allow ions to pass through the membrane, through these little pores. And we described the idea that there are-- we talked about the idea that there are many different kinds of ions, ion channels, that have different interesting properties.

So we then extended our analysis of our neuron in the dish to include these ion channels. We began by putting-- by representing ion channels as a resistance that connects the intracellular space. In the extracellular space, this resistor is in parallel with our capacitor. And we represented the current going through that resistance, which we called the "leak resistance," R sub L. We represented the current as "leak current," I sub L.

We noted that we were going to model this leak resistance using Ohm's law. So we wrote down that current, that leak current, as the membrane potential, V, divided by the leak resistance. So this is just Ohm's law.

And we also rewrote the quantity 1 over R, 1 over the resistance, as the leak conductance. So the leak current is just the leak conductance times the membrane potential. And we also introduced the idea of an I-V curve, which plots the amount of current flowing through our leak conductance here as a function of the membrane potential, this V. And for the case of a resistor, for the case where we're modeling our leak conductance with Ohm's law, the current, as a function of voltage, is a straight line going through the origin, whose slope is just the leak conductance. Any questions about that?

Then we derived a simple equation for how the membrane potential evolves over time as a function of the injected current. And we did that using Kirchhoff's current law, which says that the sum of all the currents into a node has to equal the sum of currents out of a node, where a node here means a wire. And so the sum of these occurrences equal to 0. There's a minus sign here, because this current, the electrode injected current, is defined as positive going into the cell, and these currents are defined as positive when they go out of the cell.

We substituted for the leak current, the expression from Ohm's law. So into this part of the equation here, this term, we substitute VM over R sub L. And I apologize for the slight inconsistency in notation here. Sometimes I'm using VM, and sometimes I'm using V. I'll try to fix that, but those-- VM is the same as V in what you've seen so far.

And we also have an expression here for the capacitive current. The capacitive current through this capacitor is just C, dV, dt. So we put those two expressions, make those two substitutions, and we have this expression that relates the voltage in the cell to the injected current.

We rewrote this a little bit by multiplying through by the leak resistance, and we rewrote this again making a couple substitutions. We use tau in place of RC. So that becomes a time constant. And the infinity is this expression on the right-- R leak times the injected current.

So the equation that we now have, the differential equation that we now have, for the dependence of the membrane potential on injected current looks like this-- V plus tau, dV, dt, is equal to V infinity. When we inject current into the cell, we're changing the infinity. And then the voltage evolves, as described by this differential equation.

So we're going to plot a bunch of things, the infinity and the voltage in the cell, as we inject a pulse of current. So we start out with injected current equal to 0. We step up to I naught, hold a constant injected current I naught for some period of time, and then reset the current back to 0.

So what does V infinity do as a function of time, anybody? What does that mean?

AUDIENCE: It does the same things.

MICHALE FEE: Good. It does the same thing, but multiplied by R sub L-- very good. And what does the membrane potential do? So let's start the membrane potential at 0. So starting here, what does the membrane potential do [INAUDIBLE]? Yes? What's your name?

AUDIENCE: I'm Kate.

MICHALE FEE: Kate. Yes, stays at 0.

AUDIENCE: [INAUDIBLE]

MICHALE FEE: Good. How do we say-- how do we say it? Exponentially toward V infinity, very good. So it relaxes exponentially toward infinity, which is here. And then what happens?

AUDIENCE: And then it [INAUDIBLE].

MICHALE FEE: Very good. And it does-- it relaxes with a time constant of RC. And what that means is that the time it takes for it to relax to 1 over e of its original distance from V infinity is given by tau.

Very good-- and you can solve this differential equation that was on the previous slide for periods where the injected current is constant, where V infinity is constant. And what you can see is that the voltage difference from the current V infinity relaxes exponentially to 0. It starts out at the initial voltage minus V infinity, and you multiply that difference times an exponential that decays to 0. And so the voltage difference between the voltage and V infinity decreases.

So now we then introduce the idea that neurons have batteries. Where do the batteries of a neuron come from, anybody remember? Stacey, I remember you. Where do the batteries of a neuron come from?

Good. That's what the battery produces. The battery produces a voltage difference. But biophysically, what causes that voltage difference?

AUDIENCE: [INAUDIBLE]

MICHALE FEE: Good, ion selective pores. Good, that's one component, and there's another important component. Somebody else want to answer?

AUDIENCE: Ion concentration.

MICHALE FEE: Good, excellent. So we have two components-- ion concentration gradients and ions selective pores. So basically, if you have a high concentration of potassium inside the cell, when you open up a potassium selective ion channel, the potassium ions diffuse out of the cell, leaving an excess of negative charges inside the cell that causes the voltage inside the cell to go down until there's a sufficient voltage gradient that the drift of potassium ions back into the cell driven by the voltage gradient is equal to the diffusion rate of ions out of the cell produced by the concentration gradient. At equilibrium, at the equilibrium potential, there's a particular voltage at which there is no net current into-- potassium current into or out of the cell. And that's what we mean by equilibrium potential, otherwise known as the "Nernst potential."

Last time we derived the Nernst potential using the Boltzmann equation. The Boltzmann equation gives us the ratio of the probability of finding an ion inside or outside of the cell, and that's equal to e to the minus energy difference of an ion inside and outside of the cell divided by KT. The energy difference is given by the charge times the voltage difference, the charge of the ion that we're considering times the voltage difference.

So we took the log of both sides, solved for V in minus V out, and we found that the voltage difference at equilibrium. This is at thermal equilibrium. That's what the Boltzmann equation tells us-- at thermal equilibrium.

What's the ratio of probabilities? At thermal equilibrium, the voltage difference is 25,000 millivolts times the log, the natural log, of the ratio of concentrations, and that's E sub K. If you plug-in the potassium concentrations here, that gives you the equilibrium potential for potassium or the Nernst potential for potassium.

So real neurons here on Earth are kind of like caesium neurons on that-- cesium ions on that alien planet. The potassium concentration inside of a cell is around 400 millimolar, and I think this is for squid giant axon, which is a little bit alien. Yes? Go ahead.

AUDIENCE: From the previous [INAUDIBLE].

MICHALE FEE: Yep. So if you think about the probability of finding a potassium ion inside of a cell and finding a potassium ion outside of the cell, the ratio of probabilities is going to be proportional to the ratio of concentrations. Does that make sense?

So given these concentrations, a high concentration of positive potassium ions inside the cell, a low concentration outside the cell, we can take the ratio of those concentrations, take the natural log of that. That's about 3 log units. The sign is negative, because this ratio is smaller than 1.

So the equilibrium potential for potassium is about 25 millivolts, KT over Q for a monovalent iron is 25 millivolts. So the Nernst potential is 25 millivolts times minus 3. So the equilibrium potential is about minus 75.

So let's now look at a different ion, sodium. So sodium has a very low concentration inside of a cell compared to outside. That ratio is about a factor of 10.

The natural log of 10 is about 2 log units, right? So what's the equilibrium potential for sodium, anybody has a guess?

[LAUGHS]

AUDIENCE: [INAUDIBLE]

MICHALE FEE: Yeah. Plus or minus?

AUDIENCE: Oh, plus.

MICHALE FEE: Good. So it's about 2 log units times 25 millivolts, right? So it's plus 50 or so. Good.

How about chloride? So this is interesting. Chloride is a negative ion.

It has a high concentration outside the cell and a low concentration inside the cell. So when we open up a chloride channel, what happens to the chloride ions? Which way do they go, into the cell or out of the cell?

Good. They're negative. So what is that going to do to the voltage inside the cell? We're negative, good.

And the ratio of concentrations here is about 10. So log of 10. It's 2-ish. So what's that Nernst potential going to be?

About minus 50, exactly. If you plug-in the actual numbers, it's minus 60. Great.

Good. Here's an interesting one-- calcium. Calcium is kept at an extremely low concentration inside of cells, because it's used as a signaling molecule. When calcium comes into a cell, it actually does things important.

So the cell buffers calcium. It sequesters calcium into the endoplasmic reticulum and keeps the concentration in the cytoplasm very low. The concentration outside the cell is about 2. The ratio is a pretty big number.

So if you-- OK. Why is the coefficient here, KT over Q, why is that 12 millivolts here instead of 25? Excellent. So it's KT over 2 times the electron charge. So that's 12 millivolts, very good.

And so the equilibrium potential for calcium is very positive. Great. Any questions about that?

So these are the most important ions that we have to think about in terms of ionic conductances across the membrane. Any questions? Good.

So let's go back to our neuron in the dish, and we're going to consider a neuron that has a potassium conductance and a high potassium concentration inside the cell. Remember, we can write down the magnitude of that conductance as G sub K. And now we're going to do an experiment.

We're going to measure the voltage in our cell, the steady state voltage in our cell, as a function of the amount of current that is either being injected or passing through the membrane-- its steady state. Those two things are the same. So we're going to plot the potassium current through the membrane as a function of the voltage of the cell.

So let's say that we inject 0 current. What's the steady state voltage in the cell going to be, anybody? We just went through this. Uh-oh, I have to-- oh, OK. I have a volunteer back here.

Why 25 millivolts? And we will assume the channel is open. So what is the-- so your answer is that the-- if you inject 0 current, the voltage is going to be the Nernst potential for potassium. And that is correct, but what is the actual number?

Good. It's going to be around negative 75 millivolts. So if we inject 0 current, we know a voltage of our neuron is going to be around EK or minus 75 millivolts.

Now, let's start injecting current into the cell until the voltage gets to 0. Now, are we going to be injecting positive current into this cell or negative current? What do we have to do, inject positive or negative current to make the voltage get up to 0?

Positive, right, because the voltage inside is negative. So we need to inject positive charges. And how much current do we need to inject? If the conductance is g, how much current do we need to inject?

What? V is the voltage inside of our cell, so you're getting there. You're really close. What's the answer?

A times G. So we're going to inject the current into our cell until the voltage gets to 0. And if we inject different amounts of current into the cell and measure what the voltage is, we get kind of a straight line.

So for a potassium conductance, if you hold the voltage positive above the equilibrium potential, potassium ions are going to flow out through the membrane. Is that clear? Let's hold the voltage at 0. Which way are our ions flowing? So the ions are going to be flowing out.

To hold the voltage at EK, what happens to the potassium current? It goes to 0, because you're now at the Nernst potential. And if you hold the voltage below, the inside of the cell is now negative relative to the Nernst potential, and current's going to flow in.

So notice that the current actually reverses sine around EK. And so sometimes this voltage is called the "reversal potential." So you'll hear me sometimes refer to the reversal potential, and that's just the same as the Nernst potential or the equilibrium potential.

So the equation for something that looks like this, a straight line that's offset from 0, is just this. So this expression right here is going to be our basic model for how we describe the current through an ion channel as a function of the voltage of the membrane. So current, the potassium current, is just the potassium conductance times the difference of the membrane potential from the reversal potential.

So IK equals GK times V minus EK. We also have a circuit, a little simple equivalent circuit, that describes this relation, and this is what it looks like. We have a-- what we're going to do to include the effects of this ion-specific conductance in the presence of a concentration gradient is to take our conductor, our resistor here, our conductance, and put it in series with a battery. So that's the basic circuit element that describes this kind of I-V relation.

Why is that? So let's break this down a little bit. Basically, what we're going to do is we're going to equate this membrane potential difference between the inside and the outside of the cell, this potential difference, to the sum of the voltage drops across these two elements.

Is it 1.5 volts, the same as the battery in here? No. What is it?

AUDIENCE: [INAUDIBLE]

MICHALE FEE: Yes. That's the battery we've been talking about, exactly. So the voltage drop across this battery is EK.

What's the voltage drop across this resistor, this potassium conductance? What does it depend on? What if the current is 0? What's the voltage drop across a resistor whose current is 0?

0. Ohm's law, right? What is it at arbitrary current? What's the voltage drop across a resistor as a function of current?

AUDIENCE: [INAUDIBLE]

MICHALE FEE: Good. Can somebody tell me what it is in terms of the quantities that we have? We're looking for a delta V across here.

So VM, the membrane potential, has to just equal the sum of those two voltage drops, right? So VM equals EK plus IK over GK. And now let's just solve this for IK.

So that's why this little circuit element describes our potassium conductance. That's the equation that goes with it. Any questions? No? All right, let's push on.

This quantity right here, by the way, V minus EK, is called the driving potential. If V is equal to EK, then the driving potential is 0, and there's no current. The current through the channel is proportional to the driving potential. So let's just-- so there is our new circuit diagram for our cell that's a capacitor whose membrane has little leaks in it, where there's a ion-specific permeability of the pore and ion concentration gradient to produce a battery.

There's our new circuit element. You can see that we're getting awfully close now to the whole equivalent circuit model that Hodgkin and Huxley wrote down. So let's just flesh out this equation here. What is I sub K? I sub K is just times V minus EK, very good.

Remember that the resistance, RK is just 1 over GK, and tau, again, is RK times C. So let's massage this a little bit more. We're going to write this down as V plus dV, dt equals EK plus RKIE. So what is that? Any guess what that is?

AUDIENCE: [INAUDIBLE]

MICHALE FEE: Very good. Can everyone see why that's V infinity? Because if you set dV, dt equal to 0, V is equal to IK plus RKIE. If you inject a constant current at steady state, dV, dt equals 0, you can see that the injected current is just equal to the potassium current leaking out through the membrane. That all makes great sense.

So that's V infinity. The voltage is just-- the differential equation is V plus tau dV, dt equals V infinity. It's exactly the same equation we had before. So you know that at every moment V is going to be doing what? Everybody together-- relaxing toward V infinity, right?

Where that's our new V infinity. So we're going to do the same experiment again. Here is our pulse of injected current. V infinity is now starting at EK, jumps up to EK plus RKI naught and then goes back down. And the voltage of the cell is relaxing toward V infinity.

So adding that just shifted this voltage trace down from 0. Remember, before this was sitting at 0, and now it's sitting at minus 75 millivolts. Any questions?

So we're going to come back in a minute and finish fleshing out this model where we make those conductances is dependent on time as a way of describing the spikes that a neuron produces. But before we do that, we're going to talk about a much simpler model of how a spiking neuron behaves. Basically, what we're going to do is we're going to instead of write down a detailed biophysical model of action potentials, which is where we're heading, we're just going to ask some simpler questions about how a spiking neuron behaves.

So notice that action potentials are really important. They're the way neurons communicate with other neurons. They send a signal down their axon, release neurotransmitter on other neurons. But most of the time a neuron is not spiking. What is it doing?

Well, could be. Other thoughts? Certainly sometimes it could be resting.

Right. Well, and how does it do that?

[LAUGHS]

 

It's part of it. Anybody? Yes?

Integrating its inputs, and it integrates those inputs, and eventually it spikes. So we're going to develop a model or look at a model now called, not surprisingly, "integrate and fire," that captures exactly that idea. That a neuron spends most of its time integrating its inputs, making a decision about when to spike, and then spiking, and then starting over again.

So the other crucial piece of this is that for most types of neurons the spikes are really all the same. The details of the spike wave form don't carry extra information beyond the fact that there's a spike. We're going to treat our spikes as delta functions, just discrete events at a single time, and the spikes are going to occur when the voltage in the neuron reaches a particular membrane potential, called the "spike threshold."

Now, that's a reasonable approximation for many neurons. It's not absolutely the case, but many neurons spike when the neuron reaches a particular voltage threshold. And that's captured in this model called the integrate and fire neuron.

And what we're going to do is we're going to take our Hodgkin-Huxley model, and we're going to replace these sodium and potassium conductances that actually generate the spike. We're going to replace that with a very simplified model of a spike generator, and it's going to look like this. So basically, the idea is that the cell gets input from either an electrode or from a synaptic input, and it integrates that input until it reaches a voltage, called V threshold.

And once it reaches a threshold, we simply reset the voltage back down to a lower value, called "V reset." And then we just-- if we want to, we can just draw a line at that time, and that's the spike. But what really happens to the voltage here is that once the voltage hits V threshold, it gets reset back down to this [INAUDIBLE]. Any questions?

Now, that kind of behavior is not-- it's fairly common in neurons. So this is an example of, does the voltage in a cell in motor cortex of the songbird-- and this is from a paper from Rich Mooney's lab back in 1992. And you can see that if you inject current, the voltage in this cell ramps up until it hits a threshold voltage.

It makes a spike, which is very narrow in time, but then the voltage resets down to a lower voltage. And that process just repeats over and over. So now what we're going to do is we're going to calculate the rate at which a neuron fires as a function of how much current gets injected into the cell, how much input a cell gets.

So we're going to start by considering the case where the cell has no leaks in its membrane, no conductances. So let's plot voltage as a function of time, so this is voltage as a function of time, when we inject a step of current into the cell. So what's going to happen?

So the cell starts at some voltage, and the current turns on. What's going to happen? Some fresh [INAUDIBLE]. Yes?

AUDIENCE: [INAUDIBLE]

MICHALE FEE: Excellent. Like that?

AUDIENCE: Yes.

MICHALE FEE: Very good. Then what's going to happen? Yeah. Excellent-- like that. And then what's going to happen?

AUDIENCE: [INAUDIBLE]

MICHALE FEE: So we inject a constant current into our cell, and now our cell is going to generate spikes, action potentials, at regular intervals. And the interval between those spikes is going to be controlled by how long it takes that capacitor to charge up from the reset voltage to the threshold. So we can actually just very simply calculate the firing rate of this neuron as a function of how much current we inject into the cell.

So the firing rate is just 1 over that interval between the spikes. So now what do we do? Anybody want to guess what the next step is?

How do we figure out how long it takes? We know this distance. This is kind of like some third grade word problem here. Come on, somebody help me out.

You cross a river. You're paddling one second. The river's 10 meters across. Anybody, anybody?

How about right there, white shirt, what do you think? Yes.

[LAUGHS]

 

Well, we're trying to calculate the time it takes for the voltage to go from here to here. What would it depend on? Yes?

Yeah. Well, what are you doing? Yeah, but what are you-- you're calculating what?

AUDIENCE: Delta t.

MICHALE FEE: Yeah, you're calculating delta t. And you're using what about this line? Slope, exactly.

So if we knew the slope of this line, we could calculate how long it takes to go from here to here. So let's do that. So we have this equation, C, dV, dt equals I sub E. What's the slope of this line?

Yeah, it's just dV, dt. Good. So it's dV, dt.

That's delta V over delta t. Delta V is just this voltage difference, right? And delta t is what we're trying to calculate.

So we just solve-- we just plug this into here, and we just solve for 1 over delta t. And that's just C delta V times the injected current. That's probably what you were saying, right? Any questions about that?

So let's look at what that looks like. The firing rate is proportional to the projected current. It goes through 0. At 0 injected current, the voltage is constant and the neuron will never fire. But if we inject a tiny bit of current, the voltage will slowly ramp up, and it will eventually hit the threshold and then reset.

So the firing rate is proportional to the injected current slope 1 over C delta V. If the capacitor is much bigger, what happens to the firing rate? It slows down, because as you inject current, the voltage increases more slowly because the capacitance is bigger.

Now, let's add our leak conductance back in. So this leak conductance, we're going to think of it as a potassium conductance. So I'm going to call it "G leak," because I'm going to use something like that later in Hodgkin-Huxley model, but you should think about it just as a potassium conductance.

So what's going to happen? Let's go to our plot of voltage as a function of time during our injected current. Let's say that we start at V reset, our voltage at V reset. Or actually, let's start it E leak. Now what happens, anybody? Yes?

AUDIENCE: It relaxes [INAUDIBLE].

MICHALE FEE: Good. The voltage starts here, because there's 0 injected current. As soon as you inject current, V infinity jumps up to here, let's say. The voltage relaxes exponentially toward V infinity until it hits the threshold-- very good.

Then what happens? Somebody else. Yeah? How about you in the gray shirt.

AUDIENCE: It drops.

MICHALE FEE: Great. So if you know the answer, raise your hand. We'll go much faster.

So at this point, it will jump back down to where? Good. And then what. Anybody else?

If you know the answer, raise your hand. Let's just do an exercise. Raise your hand, everybody who knows-- up high. Raise your hand up high. Now, one of you say it.

[LAUGHTER]

 

Everybody, say it.

AUDIENCE: It's relaxes.

MICHALE FEE: Great, music to my ears. It relaxes exponentially back V infinity until it hits threshold and it jumps back. It keeps doing it.

Now, what happens here? The current turns off. What happens?

Who knows the answer to that question? Raise your hands up high. Shout it out.

AUDIENCE: It goes back to the--

AUDIENCE: It relaxes.

MICHALE FEE: Excellent. It relaxes back to?

AUDIENCE: [INAUDIBLE]

MICHALE FEE: Why is it a leak, not V reset? When there's no current injected, that's V infinity. So that's why it relaxes back to E leak. Any questions? No?

It's pretty simple, right? So it's pretty simple. And we can actually derive the expression now for this delta t, and therefore, we can drive the equation for the firing rate as a function of injected current.

It's a little more complicated than the other one. I'm going to go through it in a little bit less detail, because the answer turns out to actually be pretty simple [AUDIO OUT]. So we're going to calculate the firing rate, which is just 1 over this delta t here.

Before we actually get into the math, what happens if v infinity is down here? Who knows the answer to that question? Raise your hands. Shout it out.

It won't spike, right? Good. So V infinity actually has to be above V threshold in order for that neuron to spike. Does that makes sense?

So something is different already, because before we found in the current we injected the cell would eventually spike. But now what we see is when we have a leak, the V infinity actually has to be above V threshold. And so that means there's going to be some threshold current below which the neuron won't spike. That's pretty cool. We can see that right away.

So I just wanted to find one quantity, called the "rheobase," and that is that current at which the neuron begins to spike. So if we start our cell at V reset, because let's say it just spiked, so it relaxes exponentially toward V infinity, but let's say that V infinity is right at threshold. So you can see that the time to reach the threshold is actually very long.

If V infinity is equal to V threshold, it will never actually reach it. Even when V infinity is equal to V threshold, the firing rate is 0. Because if you inject just a tiny bit more current, now it'll begin to spike.

It can calculate the injected current required to reach threshold. That's called the rheobase. We just set V infinity equal to V threshold, right? And we use our equation for-- that's V infinity, and we just set it equal to threshold.

Now we just derive the injected current we just solved for I sub E. That's the injected current required to make V infinity reach V threshold, and you can see that it's just G leak times V threshold minus E leak. And we call that I threshold.

So here's the way it looks. The firing rate of this neuron is 0 for low currents. As you inject more current, V infinity increases, but the cell still can't reach threshold until you inject an amount of current, such that V infinity reaches V threshold, and then it begins to spike.

And the firing rate increases rapidly, and then going up. Does that makes sense? So many neurons have that property of having a threshold current above which you have to-- below which the cell won't spike.

So now let's actually derive the equation for this firing rate as a function of injected current. So here's how we're going to do that. The cell just spiked, and we're going to calculate the amount of time before the cell spikes again.

So we're going to start the voltage at V reset. We know that at some injected current above threshold the cell relaxes exponentially to V infinity. And we're just going to calculate how long it takes equal to threshold.

So you know that that's an exponential, right? In fact, we wrote down the solution to that exponential a bunch of times. The difference from V to V infinity decreases exponentially.

But we know a bunch of these values, right? We know that we're calculating these voltages when tau equals, sorry, when t equals delta t. And we know the initial voltage, that's V reset. And we know the voltage at time delta t, and that's just equal to V threshold.

So we can just substitute those quantities into this equation. So now we have V [AUDIO OUT] minus V infinity equals V reset minus V infinity times E to the minus delta t over tau. Does that make sense? Everyone see what I just did?

We're just calculating this time that it takes the neuron to relax exponentially from V reset to V threshold. We know all these quantities, so we just stick them into this equation. And what do we solve for? Delta t, good.

So we take the natural log of-- well, we divide through by V reset minus V infinity, take the natural log, and we solve for delta t. So delta t equals minus tau, natural log, V infinity minus V threshold over V infinity minus V reset.

It's kind of messy, right? I don't know. The shape of that doesn't really leap to my mind.

So what we're going to do is actually just simplify this expression in a limit, in a limit that the injected current is large. So what happens here when the injected current is large? What gets big?

V infinity gets big, right? When you inject a lot of current, V infinity is very high. Does that make sense?

And when V infinity is really big, this expression approaches what? 1. And what is the log of 1?

AUDIENCE: 0.

MICHALE FEE: 0. So this expression, this expression approaches 1, and this expression, the log of that, approaches 0. So we can do is do a linear approximation of this turn right here.

So here's what we're going to do. We're going to work in the limit that V infinity is much bigger than V reset or V threshold. We're going to use the approximation that log of 1 plus alpha is just alpha.

So as this approaches 1, you can write it as 1 plus alpha. That whole thing there approximates to alpha. And when you do that and you solve for the firing rate, what you find is that the firing rate is just 1 over C delta V times the injected current minus the threshold current. Threshold current is just the rheobase that we calculated before.

Well, what does that look like? Well, what is the firing rate, first of all? I kind of simplified this a bit. What is the firing rate when the current is below I threshold? 0.

And then if it's above I threshold-- so this expression that I wrote right here is true only if the injected current greater than I threshold. And it's zero below that. So now, what does this look like?

The firing rate is 0 until you hit threshold. And then what? It increases--

AUDIENCE: Linearly.

MICHALE FEE: --linearly. So this equation is linearly in the injected current. The slope is actually exactly the same as it was for the case where there was no leak.

So the fine rate is 0. Once you hit the threshold, the firing rate of the neuron increases approximately linearly for large currents. And if you look down here, what you see is that the current actually-- the actual solution is that the firing rate jumps up at threshold and then tracks along the linear approximation.

So the dashed line there is the actual solution. The solid line is that linear approximation. And that right there is really a very good model for a lot of neurons.

Most neurons sort of saturate a little bit. Their firing rate kind of flattens out a little bit as you go to very high firing rates. But that's a pretty good approximation. Yes?

AUDIENCE: What's [INAUDIBLE]?

MICHALE FEE: Delta V is the difference from V reset to V threshold. Those are just parameters of the model. There was another question here. Skyler?

AUDIENCE: I had the same question.

MICHALE FEE: Same question? OK. Anything else? That's the integrate and fire neuron. That's probably the most commonly used model of neurons in neuroscience-- pretty simple.

Or I should say, that's the most commonly used model of spiking neurons. So you can actually take neurons that behave like this, and assemble them into complex networks, and study how network interactions occur with a spiking model. And this model captures most of the interesting, important behavior of spiking neurons. Question, Danny? Any other questions?

So let's come back to our Hodgkin-Huxley model, our equivalent circuit. So what we just described was a model neuron in which we replaced these sodium and potassium conductances that actually produce these action potentials with a very simple spike generator. But now what we're going to do is we're going to come back to our model, and we're going to flesh out the biophysical details that allow these two conductances right here to produce action potentials.

Now, in fact, most of the time when we model networks of neurons, we simplify the spike generator to something like an integrate and fire spike generator. But the framework that Hodgkin and Huxley developed for describing a time-dependent and voltage-dependent conductances is so powerful and commonly used to describe conductances that it's really worth understanding that mathematical description, that physical description, of ionic conductances and how they depend on voltage and time. So that's what we're going to do next.

So the first thing we do is we notice that in the Hodgkin-Huxley model we have three conductances. We have conductance which is very much like the lead conductance that we just used in the integrate and fire model. It has a reversal potential of around minus 50 millivolts, and it's just always on. It's just constant conductance.

We have these two other conductances, a sodium conductance and a potassium conductance, that are both time-dependent and voltage-dependent. Each one of those conductances as has a current associated with it, currents flowing through ion channels. The total membrane current is just the sum of all of those currents. That's just definition. The total ionic membrane current is just the sum of contributions from sodium channels, potassium channels, and a leak.

So the equation for our Hodgkin-Huxley model, again using Kirchhoff's current law, the sum of all the currents into these nodes has equal 0. So the membrane ionic current plus the capacitive current equals the injected electrode current. Now, each one of these conductances, or each one of these currents, can be written down in the same form that we developed before for our potassium conductance. It's just a, sorry, for the potassium current.

So the sodium current is just a sodium conductance times what? What is that? Driving potential, right? The driving potential for sodium.

But the sodium conductance now is voltage- and time-dependent. And it's that voltage and time dependence that gives sodium channels the properties that they need to generate action potentials. It's just analogous to what we already did before for the potassium conductance.

And here's the potassium current. It's just GK times the driving potential for potassium, and the potassium conductance is voltage- and time-dependent. Again, EK is minus 75, ENA is plus 55.

And our leak conductance, the leaked current rather, is just the leak conductance times the driving potential for the leak current. The difference is that, in this model now, the leak conductance is just constant. There's no time dependence, it's always there, and its voltage independent. Any questions about that?

So the name of the game here in understanding how this thing works is to figure out where this time dependence and voltage dependence comes from. What's that?

AUDIENCE: [INAUDIBLE]

MICHALE FEE: They're very close. The potassium equilibrium potential is always very close to minus 75. In some neurons, it might be as low as minus 95, but it's always in that range.

The sodium reversal potential is always plus 50-ish. Well, it's highly consistent across mammals, and the numbers for squid are pretty close to that as well. I think these are the numbers for squid that come from Hodgkin and Huxley. Questions?

Now, how do these things generate an action potential? That's the next question. Just in principle, how do you think about conductances like this generating action potentials?

So let's say that the conductances here are 0. We set those to 0. Those little arrows mean variable or adjustable. So we can imagine that we have our hand on the knob, and let's just turn those both down to 0.

So what's the voltage in the cell going to be? So what does the cell do? Well, if this is one of those moments where everybody knows the answer and they're just not saying it-- anybody? Skylar?

AUDIENCE: [INAUDIBLE]

MICHALE FEE: Good. So roughly, it's close to that. It's minus 50, in this case. Good.

So if these conductances are 0, then the cell is going to be sitting at the vault of this battery. There's 0 current, steady state, 0 current. The voltage drop across here is 0, because there is 0 current. And so the inside of the cell had better be sitting at that voltage of that battery, which is minus 50.

So now, what happens if we suddenly turn on a conductance? What do I mean by "turn on a conductance"? We make the resistance really small, or we make the conductance really big.

So what are we doing? Let's turn that conductance on as much as possible, which means we're setting that resistor to 0. Actually, if this resistance is 0, then the voltage drop across-- the voltage inside has to just be-- it has to be set to the voltage of that battery. Does that make sense?

Well, if we have no conductance here, then the voltage inside the cell will relax toward e sub l. But if we now turn on this conductance, we set that resistor to 0, the voltage will jump up that resistor back up to some big value. What's the voltage going to do? Relax back to e sub l.

So Daniel made this nice simulation of what happens. So here's what is going to happen. These conductances are going to start at 0. We're going to-- oh, wait.

These conductances are to start at 0, and then we're going to make this resistor small-- not 0, but small. Then we're going to make this resistor big, and we're going to make that resistor small. So watch what happens.

So the conductances are going to be plotted along the bottom, and the voltage of the cell is going to be plotted as a function of time here. And the green and red show the reversal potentials for the sodium and potassium. There, the sodium conductance just got turned on.

And what happened? The voltage of the cell jumps up to [INAUDIBLE] when we turn on the potassium conductance, and we turn off the sodium conductance, and the voltage gets dragged down to EK. Then when we turn off the potassium conductance, the voltage relaxes back up to [INAUDIBLE].

So look, conductances are just knobs that allow the cell to control its voltage-- an anthropomorphic way to put it. You can control the voltage of the cell just by setting the values of those resistors. If you make this resistor really small and that resistor big, the voltage jumps up toward [INAUDIBLE].

Why is that? Because you're connecting the inside of the cell to that battery. Turn that off, and then turn on this conductance, or setting that resistor to be very small, now you're connecting the inside of your cell to this battery, which is negative, down here. So you can just control the voltage of the cell up and down just by twiddling these knobs.

Another way to think about it is this. If this resistor is big, and if you set that resistor to be really small, then the voltage here dominates. So over the timescale of any process that we're considering here, the ionic concentrations inside the cell and outside of the cell don't change. Does that make sense? Yes?

AUDIENCE: So if we set both of them?

MICHALE FEE: So you set both of these to 0?

AUDIENCE: Not 0. [INAUDIBLE]

MICHALE FEE: Yeah.

AUDIENCE: [INAUDIBLE]

MICHALE FEE: If the conductance is really high, that means setting the resistors really small.

AUDIENCE: Exactly.

MICHALE FEE: That's a great question. What happens?

AUDIENCE: [INAUDIBLE]

MICHALE FEE: Exactly.

AUDIENCE: Isn't that like--

MICHALE FEE: That's exactly right. If you set both of these, if you turn on both of these conductances, then the voltage goes somewhere in the middle. And the voltage that it goes to is actually-- you have to [AUDIO OUT].

The Nernst potential that we calculated is calculated only for the case where you have one ion. If you want to calculate the equilibrium potential when you have multiple pores open, then you have to use a different method of calculating. You have to actually calculate the currents flowing in each one of those channels, and based on the permeabilities of the channels, and you get a different expression, called the Goldman-Hodgkin-Katz equation.

But the bottom line is, if you open up both of those conductances, it's somewhere in the middle. And if you want to get the exact right answer, you have to use the GHK equation. Yes?

AUDIENCE: [INAUDIBLE]

MICHALE FEE: Almost. We're not quite there yet. We're going to get there. But you can see what happens here is that these conductances are actually voltage-dependent.

So for example, the sodium conductance turns on at higher voltages. When this conductance starts getting bigger, what happens to the voltage in the cell? It starts going up, right?

But if this is voltage-dependent and it turns on at a higher voltage, what happens to the conductance? When the voltage gets a little bit bigger, what happens to the conductance, which does what to the voltage? Makes it go up even faster, right?

And so you get this runaway process where the disconductance turns on very quickly and the voltage jumps up. That's the essence of the action potential. But the essential picture that I wanted you to get from this slide is that these are just knobs. And when you turn the knobs, you can change the volt-- that controls the voltage in the cell.

Each one of these is causing the cell to be dragged toward its reversal potential. So if this conductance is big, this conductance is big, the voltage in the cell gets dragged toward ENA. If the conductance is big, the voltage in the cell gets dragged toward EK.

And next time, we're going to go through the process. We're going to describe the process to drive the voltage dependence of those ion channels, the sodium and potassium ion channels, to derive the voltage dependence and the time dependence that explains how you get this action potential in a neuron. So that's next Tuesday.