11. Spectral Analysis Part 1

• Download English-US transcript (PDF)

MICHALE FEE: So who remembers what that's called? A spectrograph. Good. And it's a spectrogram of me.

Good morning, class.

OK. So it's a spectrogram of speech. And so we are going to continue today on the topic of understanding-- developing methods for understanding how to characterize and understand temporally structured signals. So that is the microphone recording of my voice saying "good morning, class." And then this is a spectrogram of that signal where at each moment in time, you can actually extract the spectral structure of that signal.

And you can see that the information in speech signals is actually carried in parts of the signal in the way the power in the signal at different frequencies changes over time. And your ears detect these changes in frequency and translate that into information about what I'm saying.

And so we're going to today start on a-- well, we sort of started last time, but we're really going to get going on this in the next three lectures. We're going to develop a powerful set of tools for characterizing and understanding the temporal structure of signals. So this is the game plan for the next three lectures.

Today we're going to cover Fourier series-- complex Fourier series. We're going to extend that to the idea of the Fourier transform. And then so the Fourier transform is sort of a very general mathematical approach to understanding the temporal structure of signals. That's more of a-- you think of that more in terms of doing analytical calculations or sort of conceptual understanding of what Fourier decomposition is.

But then there's a very concrete algorithm for characterizing spectral structure of signals called the fast Fourier transform. And that's one class of methods where you sample signals discretely in time and get back discrete power at discrete frequencies. So that's called a discrete Fourier transform. And most often that's used to compute the power spectrum of signals. And so that's what we're going to cover today.

And then in the next lecture, we're going to cover a number of topics leading up to spectral estimation. We're going to start with the convolution theorem, which is a really powerful way of understanding the relationship between convolution in the time domain and multiplication of things in the frequency domain.

And the convolution theorem is really powerful, allowing you to kind of think about, intuitively understand the spectral structure of different kinds of signals that you can build by convolving different sort of basic elements. So if you understand the Fourier decomposition of a square pulse and a train of pulses or a Gaussian, you can basically just by kind of thinking about it figure out the spectral structure of a lot of different signals by just combining those things sort of like LEGO blocks. It's super cool.

We're going to talk about noise and filtering. We're going to talk about the Shannon-Nyquist sampling theorem, which tells you how fast you have to sample a signal in order to perfectly reconstruct it. It turns out it's really amazing. If you have a signal in time, you can sample that signal at regular intervals and perfectly reconstruct the signal if that signal doesn't have frequency components that are too high. And so that's captured in this Shannon-Nyquist sampling theorem.

That turns out to actually be a topic of current debate. There was a paper published recently by somebody claiming to be able to get around the sampling theorem and record neural signals without having to guarantee the conditions under which the Shannon-Nyquist sampling theorem claims. And Markus Meister wrote a scathing rebuttal to that basically claiming that they're full of baloney. And so those folks who wrote that paper maybe should have taken this class. So anyway, you don't want to be on the wrong end of Markus Meister's blog post. So pay attention.

So then we're going to get into spectral estimation. Then in the last lecture, we're going to talk about spectrograms. We're going to talk about how to compute spectrograms and understand really how to take the data and break it into samples called windowing, how to multiply those samples by what's called a taper to avoid contaminating the signal with lots of noise that's unnecessary.

We're going to understand the idea of time bandwidth product. How do you choose the width of that window to emphasize different parts of the data? And then we're going to end with some advanced filtering methods that are commonly used to control different frequency components of signals in your data. So a bunch of really powerful things.

Here's what we're going to talk about today. We're going to continue with this Fourier series. We started with symmetric functions last time. We're going to finish that and then talk about asymmetric functions. We're going to extend that to complex Fourier series, introduce the Fourier transform and the discrete Fourier transform and this algorithm and the fast Fourier transform, and then I'm going to show you how to compute power spectrum.

So just to make it clear, all of this stuff is basically going to be to teach you how to use one line of MATLAB. One function, FFT. Now, the problem is it's really easy to do this wrong. It's really easy to use this but not understand what you're doing and come up with the wrong answer. So all of these things that we're going to talk about today are just the kind of basics that you need to understand in order to use this very powerful function in MATLAB.

All right. So let's get started. So last time, we introduced the idea of a Fourier series. We talked about the idea that you can approximate any periodic function. So here I'm just taking a square wave that alternates between positive and negative. It's periodic with a period capital T. So it's a function of time. It's a even function or a symmetric function, because you can see that it's basically mirror symmetry around the y-axis. It's even because even polynomials also have that property of being symmetric.

We can approximate this periodic function T as a sum of sine waves or cosine waves, in this case. We can approximate that as a cosine wave of the same period and the same amplitude. So we can approximate as a coefficient times cosine 2 pi f0 t where f0 is just 1 over the period. So if the period is one second, then the frequency is 1 hertz, 1 over 1 second. We often use this different representation of frequency, which is usually called omega, which is angular frequency. And it's just 2 pi times this oscillation frequency. And it has units of radians per second.

So we talked about the fact that you can approximate this periodic function as a sum of cosines. We talked about the idea that you only need to consider cosines that are integer multiples of omega 0, because those are the only cosine functions, those are the only functions, that also are periodic at frequency omega 0. So a function cosine 3 omega 0 t is also periodic at frequency omega 0. Does that make sense?

So now we can approximate any periodic function. In this case, any even or symmetric periodic function as a sum of cosines of frequencies that are integer multiples of omega 0. And each one of those cosines will have a different coefficient.

So here's an example where I'm approximating this square wave here as a sum of cosines of these different frequencies. And it turns out for a square wave, you only need the odd multiples of omega 0. So here's what this approximation looks like for the case where you only have a single cosine function. You can add another cosine of 3 omega 0 t and you can see that that function starts getting a little bit more square. You can add a cosine 5 omega 0 t. And as you keep adding those things, again, with the correct coefficients in front of these, you can see that the function more and more closely approximates the square wave that we're trying to-- yes, Habiba

AUDIENCE: Why do we only need the odd multiples?

MICHALE FEE: It just, in general, you need all the multiples. But for this particular function, you only need the odd ones.

Here's another example. So in this case, we are summing together cosine functions to approximate a train of pulses. So the signal we're trying to approximate here just has a pulse every one unit of time, one period. And you can see that to approximate this, we can basically just sum up all the cosines of all frequencies n omega 0. And you can see that at time 0, all of those functions are positive. And so all of those positive contributions to that sum all add up. And as you add them up, you get a big peak. That's called constructive interference.

So all those peaks add up. And you also get those peaks all adding up one period away. One period of cosine omega 0. You can see they add up again. So you can see this is a periodic function. In this time window between those peaks, you can see that you have positive peaks of some of those cosines, negative peaks, positive, negative. They just sort of all add up. They interfere with each other destructively to give you a 0 in the intervals between the peaks. Does that make sense? And so basically, by choosing the amplitude of these different cosine functions, you can basically build any arbitrary periodic function down here. Does that makes sense?

All right. There's one more element that we need to add here for our Fourier series for even functions. Anybody have any idea what that is? Notice here I've shifted this function up a little bit. So it's not centered at 0. A constant term. What's called a DC term. We basically take the average of that function. We add it here. That's called a DC term. a 0 over 2 is essentially the average of the function we're trying to approximate. All right. Good.

We can now write that as a sum. y even of t equals a0 over 2 plus a sum over all these different n's of a sub n, which is a coefficient, times cosine n omega 0 t. Omega 0 is 1 over-- is 2 pi over this time interval here, the periodicity. All right. Good.

How do we find those coefficients? So I just told you that the first coefficient, the a 0 over 2, is just the average of our function t over one time window from minus t over 2 to plus t over 2. It's just the integral of that function over one period divided by t. And that gives you the average, which is a 0 over 2. All right, any questions about that? It's pretty straightforward.

What about this next coefficient, a1? So the a1 coefficient is just the overlap of our function y of t with this cosine. We're just multiplying y0 times cosine of omega 0 t integrating over time and then multiplying by 2 over t. So that's the answer. And I'm going to explain why that is.

That is just a correlation. It's just like asking how much-- let's say we had a neuron with a receptive field of cosine omega 0 t. We're asking how well does our signal overlap with that receptive field. Does that make sense? We're just correlating our signal with some basis function, with some receptive field. And we're asking how much overlap is there.

The a2 coefficient is just the overlap of the function y with cosine 2 omega 0 t. And the a sub n coefficient is just the overlap with cosine n omega 0 t. Just like that. And you can see that this average that we took up here just is the generalization of this to the overlap of our function to cosine 0 omega 0 t. Cosine 0 omega 0 t is just 1. And so this coefficient a0 just looks the same as this. It's just that in this case, it turns out to be the average of the function. Any questions about that?

So that is, in general, how you calculate those coefficients. So you would literally just take your function, multiply it by a cosine of some frequency, integrate it, and that's the answer.

Let's just take a look at what some of these coefficients are for some really simple functions. So there I've rewritten what each of those coefficients is as an integral. And now let's consider the following function. So let's say our function is 1. It's just a constant at 1. So you can see that this integral from minus t over 2 to t over 2, that integral is just t multiplied by 2 over t gives that coefficient as just 2.

If our function is cosine omega 0 t, you can see that if you put a cosine in here, that averages to 0. If you put a cosine in here, you get cosine squared. The integral of cosine squared is just half of basically the full range. So that's just t over 2. When you multiply by 2 over t, you get 1. And the coefficient a2 for a function cosine omega t is 0, because the integral of cosine omega 0 t times cosine 2 omega 0 t is 0.

All right. If we have a function cosine 2 omega 0 t, then these coefficients are 0, and that coefficient is 1. You can see that you have this interesting thing here. If your function is cosine omega 0 t, then the only coefficient that's non-zero is the one that you're overlapping with cosine omega 0 t. It's only this first coefficient that's non-zero. If your function has a frequency 2 omega 0 t, then the only coefficient that's non-zero is the a2.

So what that means is that if the function has maximal overlap, if it overlaps one of those cosines, then it has 0 overlap with all the others. And we can say that set of cosine functions, cosine omega 0 t, cosine 2 omega 0 t, forms what's called an orthogonal basis set. We're going to spend a lot of time talking about basis set later, but I'm just going to throw this word out to you so that you've heard it when I come back to the idea of basis sets later. You're going to see this connection.

So the basic idea is that what we're doing is we're taking our signal, which is a vector. It's a set of points in time. We can think of that as a vector in a high dimensional space. And we're simply expressing it in a new basis set of cosines of different frequencies. So each of those functions, cosine n omega t, is like a vector in a basis set. Our signal like a vector.

And what we're doing is when we're doing these projections, we're simply computing the projection of that vector, our signal, onto these different basis functions, these different basis vectors. So we're just finding the coefficient so that we can express our signal as a sum of a coefficient times a basis vector plus another coefficient times another basis vector and so on.

So for example, in the simple standard basis where this vector is 0 1 and that vector is 1 0, you can write down an arbitrary vector as a coefficient times this plus another coefficient times that. That make sense? And how do we find those coefficients? We just take our vector and dot it onto each one of these basis vectors, x2. Does that make sense?

You don't need to know this for this section, but we're going to come back to this. I would like you to eventually kind of combine these views of taking signals and looking at projections of those into new basis sets. And as you know, how you see things depends on how you're looking at them, the direction that you look at them.

That's what we're doing. When we take a signal and we project it onto a function, we're taking a particular view of that function. So as you know, the view you have on something has a big impact on what you see. Right?

So that's all we're doing is we're taking functions and finding the projection on which we can see something interesting. That's it. That's all spectral analysis is. And the particular views we're looking at are projections onto different periodic functions. Cosines of different frequencies. All right? And what you find is that for periodic signals, there are certain views where something magically pops out and you see what's there that you can't see when you just look at the time domain.

All right. So we looked at even functions or symmetric functions. Now let's take a look at odd functions are antisymmetric functions. These are called odd because the odd polynomials like x cubed looks like this. If it's negative on one side, it's positive on the other side. Same here. If it's negative here, then it's positive there.

So we can now write down Fourier series for odd or antisymmetric functions. What do you think we're going to use? Instead of cosines, we're going to use sines, because sines are symmetric around-- antisymmetric around the origin. And we're still going to consider functions that are periodic with period t. We can take any antisymmetric function and approximate it as a sum of sine waves of frequency 2 pi over t or, again, omega 0. And integer multiples of that omega 0.

All right. So again, our odd functions can be approximated as a sum of components, contributions of different frequencies with a coefficient times sine of omega 0 t plus another coefficient times sine of 2 omega 0 t and so on. And we can write that as a sum that looks like this. So a sum over n from 1 to infinity of coefficient b sub n times sine of n omega 0 t. And why is there no DC term here? Good. Because an antisymmetric function can't have a DC offset.

So for arbitrary functions, you can write down any arbitrary periodic function as the sum of a symmetric part and an antisymmetric part. So we can write down an arbitrary function as a sum of these cosines plus a sum of sine waves. So that's Fourier series. Any questions about that?

So this is kind of messy. And it turns out that there's a much simpler way of writing out functions as sums of periodic functions. So rather than using cosines and sines, we're going to use complex exponentials. And that is what complex Fourier series does. All right, so let's do that.

So you probably recall that you can write down a complex exponential e to the i omega t as a cosine omega t plus i sine omega t. So e to the i omega t is just a generalization of sines and cosines. So the way to think about this is e to the i omega t is a complex number. If we plot it in a complex plane where we look at the real part along this axis, the imaginary part along that axis, e to the i omega t just lives on this circle. No matter what omega t is, e to the i omega t just sits on this circle in the complex plane, the unit circle in the complex plane. e to the i omega t is a function of time.

It simply has a real part that looks like cosine. So the real part of this as you increase t or the phase omega t is the real part just oscillates sinusoidally back and forth like this as a cosine. The imaginary part just oscillates back and forth as a sine. And when you put them together, something that goes back and forth this way as a cosine and up and down that way as a sine just traces out a circle.

So e to the i omega traces out a circle in this direction, and as time increases, it just goes around and around like this. E to the minus i omega t just goes the other way. That make sense? Got the real part that's going like this, the imaginary part that's going like this. And you put those together and they just go around in a circle. So you can see it's a way of combining cosine and sine together in one function.

So what we're going to do is we're going to rewrite our Fourier series as instead of sines and cosines, we're going to stick in e to the-- we're going to replace the sines and cosines with e to the i omega t and e to the minus i omega t. So we're just going to solve these two functions for cosine and sine, and we're going to take this and plug it into our Fourier series and see what we get. So let's do that. And remember, 1 over i is just minus i.

So here's our Fourier series with our sum of cosines, our sum of sines. We're just going to replace those things with the e to the i omega t plus e to the minus i omega t and so on. So there we go. Just replacing that. There's a 1/2 there. And now we're just going to do some algebra. And we're going to collect either the i omega t's and e to the minus i omega t's together. And this is what it looks like.

So you can see that what we're doing is collecting this into a bunch of terms that have e to the positive in omega t here and e to the minus in omega 0 t there. And now we have still a sum of three things. So it doesn't really look like we've really gotten anywhere. But notice something. If we just put the minus sign into the n, then we can combine these two into one sum. And this, if n is 0, what is e to the in omega t? It's just 1.

So we can also write this as something e to the in omega t as long as n is 0. So that's what we do. Oh, and by the way, these coefficients here we can just rewrite as sums of those coefficients up there. Don't worry. This all looks really complicated. By the end, it's just boiled down to one simple thing. That's why we're doing this. We're simplifying things.

So when you do this, when you rewrite this, this looks like a sum over n equals 0. This is a sum over positive n, n equals 1 to infinity. This is a sum over negative n, minus 1 to minus infinity. And all those combine into one sum. So now we can write down any function y of t as a sum over n equals minus infinity to infinity of a coefficient a sub n times e to the in omega.

So we went from having this complicated thing, this sum over our constant terms, sines, and cosines, and we boiled it down to a single sum. That's why these complex exponentials are useful. Because we don't have to carry around a bunch of different functions, different basis functions to describe an arbitrary signal y. But remember, this is just a mathematical trick to hide sines and cosines. A very powerful trick, but that's all it's doing. It's hiding sines and cosines.

All right. So we've replaced our sums over coastlines and signs with a sum of complex exponentials. All right. Remember what we're doing here. We're finding a new way of writing down functions. So what's cool about this, what's really interesting about this, is that for some functions-- so what we're doing is we have an arbitrary function y. And we're writing a down with just some numbers a sub n. And what's cool about this is that for some functions y, you can describe that function with just a few of these coefficients a. Does that make sense?

So let me just show you an example of some functions that look really, really simple when you rewrite them using these coefficients a. So here's an example. So here's a function of n that has three numbers. a sub minus 1, n equals minus 1 is 1/2, a sub 0 is 0, and a sub 1 is 1/2. And all the rest of them are 0. So really, we only have two non-zero entries in this sum.

So what function is that? It's just a cosine. So we have-- let's write this out. Y equals a sum over all of these things. 1/2 e to the minus-- the first n is minus 1. e to the minus i omega 0 t plus 1/2 e to the plus i omega 0 t. We're just writing out that sum. And that is just-- sorry, I didn't tell you what that equation was. That's Euler's equation. That's just cosine minus i sine omega t. That is just cosine plus i sine omega t. The sines cancel. And you're left with cosine omega 0 t.

So here's this function of time that goes on infinitely. If you wanted to write down all the values of cosine omega 0 t, you'd have to write down an awful lot of numbers. And here we can write down that same function with two numbers. So this is a very compact view of that function of time.

Here's another function. What function do you think that is? What would be the time domain equivalent of this set of Fourier coefficients? Good. So we're going to do the same thing. Just write it out. All these sums are 0. All these components are 0 except for two of them. n equals minus 2 and n equals plus 2. You just put those in there as 1/2 e to the minus 2 omega 0 t plus 1/2 e to the plus 2 omega 0 t. And that is just if you write that out, those sines cancel, and you have cosine 2 omega 0 t. Pretty simple, right?

How about this one? This is the-- remember, the a's are complex numbers. The ones we were looking at here had two real numbers. Here's an example where the a's are imaginary. One is i over 2. One is minus i over 2. That's what the complex Fourier representation looks like of this function. We can just plug it in here.

You solve that, you can see that in this case, the cosines cancel, because this is i over 2 cosine 2 omega t minus i over 2 cosine 2 omega t. Those cancel and you're left with sine 2 omega 0 t. So that is what Fourier representation of sine 2 omega t looks like. So the functions that have higher frequencies will have non-zero elements that are further out in n. Any questions about that?

So again, this set of functions e to the in omega 0 t form an orthogonal, orthonormal basis set over that [INAUDIBLE] over that interval. The a0 coefficient is just the projection of our function onto e to the 0. n equals 0. And that's just the average. The a1 coefficient is just the projection of our function e to the minus i omega 0 t. And in general, the m-th coefficient is just the projection of our function onto e to the minus im omega 0 t.

And we can take those coefficients, plug them into this sum, and reconstruct an arbitrary periodic function, this y of t. So we have a way of taking a function and getting these complex Fourier coefficients. And we have a way of taking those coefficients and reconstructing our function. This is just a bunch of different views function y. And from all of those different views, we can reconstruct our function. That's all it is.

So in general, when we do Fourier decomposition in a computer in MATLAB on real signals that you've sampled in time, it's always done in this kind of discrete representation. You've got, in this case, discrete frequencies. When you sample signals, you've got functions that are discrete in time, and this becomes a sum. But before we go to the discrete case, I just want to show you what this looks like when we go to the case of arbitrary functions. Remember, this thing was about representing periodic functions. You can only represent periodic functions using these Fourier series.

But before we go on to the Fourier transform algorithm and discrete Fourier transforms, I just want to show you what this looks like for the case of arbitrary functions. And I'm just showing this to you. I don't expect you to be able to reproduce any of this. But you should see what it looks like, for those of you who haven't seen it already.

So what we're going to do is go from the case of periodic functions to non-periodic functions. And the simplest way to think about that is a periodic function does something here, and then it just does the same thing here, and then it just does the same thing here. So how do we go from this to an arbitrary function? Well, we're just going to let the period go to infinity. Does that make sense?

That's actually pretty easy. We're going to let t go to infinity, which means the frequencies, which are 2 pi omega 0 or 2 pi over t, that's going to go to 0. So our steps. Remember when we had this discrete Fourier transform here, we had these steps in frequency as a function of n. Those steps are just going to get infinitely close together, the different frequency bins.

So that's what we're going to do now. You're just going to let those frequency steps go to 0. And now frequency, in discrete case, the frequency is just that number, that n times omega 0. m times omega 0. Well, omega 0 is going to 0, but the m's are getting really big. So we can just change-- we're just going to call that omega. The omega 0's are going to 0, so the m's are getting infinitely big. So we can't really use m anymore or n to label our frequency steps. So we're just going to use omega.

We used to call our coefficients, our Fourier coefficients, we used to label them with m. We can't use m anymore, because m is getting infinitely big. So we use this new label omega. So a sub m becomes a new variable, our Fourier transform, labeled by the frequency omega. And we're just going to basically just make those replacements in here. So the coefficients become a function of frequency. That's just an integral. Remember, t is going to infinity now.

So this has to go from minus infinity to infinity of our function y times our basis function. And instead of e to the im omega 0 t, we just replace m omega 0 with omega. So e to the minus i omega t. And that is the Fourier transform. And we're just going to do the same replacement here, but instead of summing over n going from minus infinity to infinity, we have to write this as an integral as well.

And so that we can reconstruct our function y of t as an integral of our Fourier coefficients times the e to the i omega t. See that? It's essentially the same thing. It's just that we're turning this sum into an integral. All right. So that's called a Fourier transform. And that's the inverse Fourier transform, this [INAUDIBLE] from a function to Fourier coefficients. And this takes your Fourier coefficients and goes back to your function. All right, good.

Let me just show you a few simple examples. So let's start with the function y of t equals 1. So it's just a constant. What is the Fourier transform? So let's plug this into here. Does anyone know what that integral looks like of the integral from minus infinity to infinity of e the minus i omega t dt integrating over time. It's a delta function. There's only one value of omega for which that function is not 0.

Remember, so let's say omega equals 1, 1-- you know, 1 hertz. This is just a bunch of sines and cosines. So when you integrate over sines and cosines, you get 0. Integral over time of cosine is just 0. But if omega is 0, then what is e to the i omega t? e to the i 0 is 1. And so we're integrating over 1 times dt. And that becomes infinity at omega equals 0. And that's a delta function, it's 0 everywhere except 4 at 0.

So that becomes a delta function. This Fourier transform of a constant is a delta function. And that's a really-- it's a really good one to know. The Fourier transform of a constant is a delta function. That's called a Fourier transform pair. You have a function and another function. One function is the Fourier transform of the other function that's called a Fourier transform pair.

So the Fourier transform of a constant is just a delta function at 0. You can invert that. If you integrate, let's just plug that delta function into here. If you integrate delta function times e to the i omega t, you just get e to the i 0t, which is just 1. So we can take the Fourier transform of 1, get a delta function, [INAUDIBLE] inverse Fourier transform the delta function, and get back 1.

How about this function right here? This function is e to the i omega 1. It's a sine wave and a cosine wave, a complex sine and cosine, at frequency omega 1. Anybody know what the Fourier transform of that is?

AUDIENCE: [INAUDIBLE]

MICHALE FEE: Yeah. So it's basically-- you can think of this-- that's the right answer. Rather than try to explain it, I'll just show you. So the Fourier transform of this is just a peak at omega 1. And we can inverse Fourier transform that and recover our original function. So those last few slides are more for the aficionados. You don't have to know that. We're going to spend time looking at the discrete versions of these things.

How about this case? This is a simple case where you have a function that the Fourier transform of which has a peak at omega 1 and a peak at minus omega 1. The Fourier transform of the inverse Fourier transform of that is just cosine omega 1t. So a function, a cosine function with frequency omega 1, has two peaks, one at frequency omega 1 and another one at frequency minus omega 1. So that looks a lot like the case we just talked about where we had this complex Fourier series.

And we had a peak at n equals 2 and another peak at n equals minus 2. And that function that gave us that complex Fourier series was cosine 2 omega t. So that's just what we have here. We have a peak in the spectrum at omega 1, peak at minus omega 1, and that is the Fourier decomposition of a function that is cosine omega 1t. So it's just like what we saw before for the case of the complex Fourier series. So that was Fourier transform.

And now let's talk about the discrete Fourier transform and the associated algorithm for computing that very quickly called the Fast Fourier Transform, or FFT. So you can see computing these Fourier transforms, if you were to actually try to compute Fourier transforms by taking a function, multiplying it by these complex exponentials like writing down the value of e to the i omega t at a bunch of different omegas and a bunch of different t's and then integrating that numerically, that would take forever computationally.

But it turns out that there's-- so you have to compute that integral over time for every omega that you're interested in. It turns out really, really fast algorithm that you can use for the case where you've got functions that are sampled in time and you want to extract the frequencies of that signal at a discrete set of frequencies. I'm going to switch from using omega, which is very commonly used when you're talking about Fourier transforms, to just using f, the frequency. So it's just f is just 2 pi. So omega is 2 pi f.

So here I'm just rewriting the Fourier transform and the inverse Fourier transform with f rather than omega. So we're going to start using f's now for the discrete Fourier transform case. And we're going to consider the case where we have signals that are sampled at regular intervals delta t. So here we have a function of time y of t. And we're going to sample that signal at regular intervals delta t. So this is delta t right here. That time interval there. So the sampling rate, the sampling frequency, is just 1 over delta t.

So the way this works in the fast Fourier transform algorithm is you just take those samples and you put them into a vector in MATLAB, just some one-dimensional array. And we're going to imagine that our samples are acquired at different times. And let's [INAUDIBLE] minus time step 8, minus 7, minus 6. Time step 0 is in the middle up to time step 7.

And we're going to say that N is an even number. The fast Fourier transform works much, much faster when N is an even number, and it works even faster when N is a multiple, a power of 2. So in this case, we have 16 samples. It's 2 to the 4. Should usually try to make your samples be a power of 2. The number of samples. So there is our function of time sampled at regular intervals t.

So you can see that the t min, the minimum time, in this vector of sample points in our function is minus N over 2 delta t. And that [INAUDIBLE] time is N over 2 minus 1 times delta t. And that's what the MATLAB code would look like to generate an array of time values. Does that make sense?

The FFT algorithm returns the Fourier components of that function of time. And it returns the Fourier components in a vector that has the negative frequencies on one side and the positive frequencies on the other side and the constant term here in the middle. The minimum frequency is N over 2 times delta F. Oh, I should say it returns the Fourier components in steps of delta f where delta F is the sampling rate divided by the number of time steps that you put into it.

Don't panic. This is just reference. I'm showing you how you put the data in and how you get the data out. When you put data into the Fourier transform algorithm, the FFT algorithm, you put in data that's sampled at times, and you have to know what those times are. If you want to make a plot of the data, you need to make an array of time values. And they just go from a t min to a t max. And there's a little piece of MATLAB code that produces that array of times for you.

What you get back from the Fourier transform, the FFT, an array of not values of the function of time, but rather an array of Fourier coefficients. Just like we stuck in into our-- when we did the complex Fourier series, we stuck in a function of time. And we get out a list of Fourier coefficients. Same thing here. We put in a function of time, and we get out Fourier coefficients.

And the Fourier coefficients are complex numbers associated with different frequencies. So let's say the middle coefficient that you get will be the coefficient for the constant term. This coefficient down here will be the coefficient for the minimum frequency, and that coefficient will be the coefficient for the maximum frequency, the most positive frequency. Does that make sense?

AUDIENCE: [INAUDIBLE]

MICHALE FEE: Ah, OK. So I was hoping to just kind of skip over that for now. But when you do a discrete Fourier transform, turns out that the coefficient for the most negative frequency is always exactly the same as the coefficient for the most positive frequency. And so they're just given in one-- they're both given in one element of the array. You could replicate that up here, but it would be pointless. And the length of the array would have to be n plus 1. Yes?

AUDIENCE: [INAUDIBLE]

MICHALE FEE: OK. Good. That question always comes up, and it's a great question. What we're trying to do is to come up with a way of representing arbitrary functions. So we can represent symmetric functions by summing together a bunch of cosines. We can represent antisymmetric functions by summing together a bunch of sines. But if we want to represent an arbitrary function, we have to use both cosines and sines.

So we have this trick, though, where we can, instead of using sines and cosines, using these two separate functions, we can use a single function which is a complex exponential to represent things that can be represented by sums of cosines as well as things that can be represented as sums of signs. It's an arbitrary function.

And the reason is because the complex exponential has both a cosine in it and a sine. So we can represent a cosine as a complex exponential with a positive frequency, meaning that it's a complex number that goes around this direction plus another function where the complex number is going around in this direction. So positive frequencies mean as time increases, this complex number is going around the unit circle in this direction. Negative frequencies mean the complex number's going around in this direction.

And you can see that in order to represent a cosine, I need to have-- so let's see if I can do this. Here's my e to the-- here's my plus frequency going around this way. Here's my minus frequency going around this way. And you can see that I can represent a cosine if I can make the imaginary parts cancel. So if I have one function that's going around like this, another function that's going around like this. If I add them, then the imaginary part cancels. The sine cancels. This plus this is cosine plus cosine. i sine minus i sine.

So the sines can-- the sine cancels. And what I'm left with is a sine. So represent a cosine as a sum of a function that has a positive frequency and a negative frequency. You can see that the y component, the imaginary component, cancels and all I'm left with is the cosine that's going across like this.

So it's just a mathematical trick. Positive and negative frequencies are just a mathematical trick to make either the symmetric part of the function or antisymmetric part of the function cancel. So I can just use these positive and negative frequencies to represent any function. If I only had positive frequencies, I wouldn't be able to represent arbitrary functions.

So just one more little thing that you need to know about the FFT algorithm. So remember we talked about if you have a function of time, negative times are over here, positive times are over here. You can put-- you can sample your function at different times and put those different samples into an array.

Before you send this array of time samples to the FFT algorithm, you just need to swap the right half of the array with the left half of the array using a function called time shifted arrays. Don't worry about it. It's just the guts of the FFT algorithm wants to have the positive times in the first half and the negative times in the second half. So you just do this.

Then you run the FFT function on this time shifted array. And what it spits back is an array with the positive frequencies in the first half and the negative frequencies in the second half. And you can just swap those back using the circshift again. That is your spectrum. Your spectral coefficients. Your Fourier coefficients of this function. Just MATLAB guts. Don't worry about it.

So here's a piece of code that computes the Fourier coefficients of a function. So the first thing we're going to do is define the number of points that we have in our array. 2048. So it's a power of 2. So the FFT algorithm runs fast. We're figuring out-- we're going to write down a delta t. In this case, it's one millisecond. The sampling rate, the sampling frequency is just 1 over delta t. So 1 kilohertz.

The array of times at which the function sampled is just going from minus n over 2 to plus n over 2 minus 1 times delta t. I'm defining the frequency of a sine wave. And we're now getting the values of that cosine function at those different times. Does that make sense? We're taking that function of time and circularly shifting it by half the array.

So that's the circularly shifted, the swapped values of our function y. We stick that into the FFT function. It gives you back the Fourier coefficients. You just swap it again. And that is the spectrum, the Fourier transform [INAUDIBLE] signal. And now you can write down a vector of frequencies of each one of those Fourier coefficients.

Each one of those segments in that vector y-- remember, there are 2,000 of them now, 2,048 of them-- each one of those is the Fourier coefficient of the function we put in at each one of those different frequencies. Does that make sense?

Now let's take a look at a few examples of what that looks like. So here is a function y of t. It's cosine 2 pi f 0 t where f 0 is 20 hertz. So it's just a cosine wave. You run this code on it. And what you get back is an array of complex numbers. It has a real and imaginary part as a function of frequency.

And you get this cosine function. It has two peaks, as promised. It has a peak at plus 20 hertz and a peak at minus 20 hertz. One of those peaks gives you an e to the i omega t that goes this way at 20 hertz. The other one gives you an e of the i omega t that goes this way at 20 hertz. And when you add them together, if I can do that, it gives you a cosine. It goes back and forth at 20 hertz. That one.

Here's a sine wave. y equals sine 2 pi f 0 t again at 20 hertz. You run that code on it. It gives you this. Notice that-- OK, sorry. Let me just point out one more thing. In this case, the peaks are in the real part of y. For the sine function, the real part is 0 and the peaks are in the imaginary part. There's a plus i at minus 20 i over 2, actually, at minus 20 hertz, a minus i at plus 20 hertz.

And what that does is when you multiply that coefficient times e to the i omega t and that coefficient times whichever the opposite one is. One going this way, the other one going this way. You can see that the real part now cancels. And what you're left with is the sine part that doesn't cancel. And that is this function sine omega t. Any questions about that?

That's kind of boring. We're going to put more interesting functions in here soon. But I just wanted you to see what this algorithm does on the things that we've been talking about all along. And it gives you exactly what you expect.

Remember, we can write down any arbitrary function as a sum of sines and cosines. Which means we can write down any arbitrary function as a sum of these little peaks and these peaks at different frequencies. Does that make sense? So all we have to do is find these coefficients, these peaks, what values of these different peaks to stick in to reconstruct any arbitrary function.

And we're going to do a lot of that in the next lecture. We're going to look at what different functions here look like in the Fourier domain. We're going to do that for some segments like a square pulse, for trains of pulses, for Gaussian, for all kinds of different functions. And then using the convolution theorem, you can actually just predict in your own mind what different combinations of those functions will look like.

So I want to end by talking about one other really critical concept called the power spectrum. And it's basically usually what you do when you compute the Fourier transform of a function is to figure out what the power spectrum is. The simple answer is that all you do is you square this thing. Take the magnitude squared. But I'm going to build up to that a little bit.

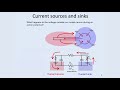
So it's called the power spectrum. But first we need to understand what we mean by power. So we're going to think about this in the context of a simple electrical circuit. Let's imagine that this function that we're computing the Fourier transform of, imagine this function is voltage. That's where this idea comes from. Imagine that this function is the voltage that you've measured somewhere in a circuit. Let's say in this circuit right here. Or current, either way.

So when you have current flowing through this circuit, you can see that sinusoid-- that some oscillatory current, some cosine, that drives current through this resistor. And when current flows to a resistor, it dissipates power. And the power dissipated in a resistor is just the current times the voltage drop across that resistor. That means that the power-- now, remember, Ohm's law tells you that current is just voltage divided by resistance. So this is v divided by r. So the power is just v squared divided by r.

So if the voltage is just a sine wave at frequency omega, then v is some coefficient, some amplitude at that frequency times cosine omega t. We can write that voltage using Euler's equation as 1/2 e to the minus i omega t plus 1/2 e to the plus i omega t.

And let's calculate the power associated with that voltage. Well, we have to average over one cycle of that oscillation. So the average power is just given by the square magnitude of the Fourier transform [INAUDIBLE]. So let's just plug this into here. And what you see is that the power at a given frequency omega is just that coefficient magnitude squared over resistance times 1/2 e to the minus i omega t magnitude squared plus 1/2 e to the plus i over i omega t magnitude squared.

And that's just equal to 1 over r. That coefficient magnitude squared over 2. So you can see that the power dissipated by this sinusoidal voltage is just that magnitude squared over 2. So we can calculate the power dissipated in any resistor simply by summing up the [INAUDIBLE] magnitude of those coefficients.

So let's look at that in a little more detail. So let's think for a moment about the energy that is dissipated by a signal. So energy is just the integral over time. Power is per unit time. Total energy is just the integral of the power over time. So power is just equal to v squared over r. So I'm just going to substitute that in there. So the energy of a signal is just 1 over r times the integral of v squared over time.

Now, there's an important theorem in complex analysis called Parseval's theorem that says that the integral over the square of the coefficients in time is just equal to the integral of the square magnitude coefficients in frequency. So what that's saying is that it's just the same as the total power in the signal or the total energy in a signal if you represent it in the time domain is just the same as the total energy in the signal if you look at it in the frequency domain.

And what that's saying is that the sum of all the squared temporal components is just this equal to the sum of all the squared frequency components. And what that means is that you can see that each of these frequency components, each component in frequency contributes independently to the power in the signal. What that means is that you can think-- so you can think of the total energy in the signal as just the integral over all frequencies of this quantity here that we call the power spectrum.

And so we'll often take a signal, calculate the Fourier components, and plot the area of the Fourier transform, the square magnitude of the Fourier transform. And that's called the power spectrum. And I've already said the total variance of the signal in time is the same as the total variance of the signal in the frequency domain. So mathy people talk about the variant of a signal. The more engineering people talk about the power in the signal. But they're really talking about the same thing.

So let's take this example that we just looked at and look at the power spectrum. So that's a cosine function. It has these two peaks. Let me just point out one more important thing. For real functions, so in this class, we're only going to be talking about real functions of time.

For real functions, the square magnitude of the Fourier transform is symmetric. So you can see here if there is a peak in the positive frequencies, there's an equivalent peak in the negative frequencies. So when we plot the power spectrum of a signal, we always just plot the positive side.

And so here's what that looks like. Here is the power spectrum of a cosine signal. And it's just a single peak. So in that case, it was a cosine at 20 hertz. You get a single peak at 20 hertz.

What does it look like for a sine function? What is the power spectrum of a sine function? Remember, in that case, it was the real part was 0 and the imaginary part had a plus peak here and a minus peak here. What does the spectrum of that look like? Right. The square magnitude of i is just 1.

Magnitude squared of i is just 1. So the power spectrum of a sine function looks exactly like this. Same as a cosine. Makes a lot of sense. Sine and cosine are exactly the same function. One's just shifted by a quarter period. So it has to have the same power spectrum. It has to have the same power.

Let's take a look at a different function of time. Here's a train of delta functions. So we just have a bunch of peaks spaced regularly at some period. I think it was-- I forget the exact number here. But it's around 10-ish hertz. Fourier transform of a train of delta functions is another train of delta functions. Pretty cool. The period in the time domain is delta t. The period in the Fourier domain is 1 over delta t. That's another really important Fourier transform pair for you to know.

So the first Fourier transform pair that you need to know is that a constant in the time domain is a delta function in the frequency domain. A delta function in the time domain is a constant in the frequency domain. A train of delta functions in the time domain is a train of functions in the frequency domain and vice versa.

And there's a very simple relation between the period in the time domain and the period in the frequency domain. What does the power spectrum of this train of delta functions look like? It's just the square magnitude of this. So it just looks like a bunch of peaks.

So here's another function. A square wave. This is exactly the same function that we started with. If you look at the Fourier transform of the imaginary part of 0, the real part has these peaks. So the Fourier transform-- so these are now the coefficients that you would put in front of your different cosines at different frequencies to represent the square wave. But what it looks like is positive peak for the lowest frequency, negative peak for the next harmonic, positive peak, and gradually decreasing amplitudes.

The power spectrum of this-- oh, and one more point is that if you look at the Fourier transform of a higher frequency square wave, you can see that those peaks move apart. So you can transform. So higher frequencies in the time domain, stuff happening faster in the time domain, is associated with things moving out to higher frequencies in the frequency domain. You can see that the same function higher frequencies has the same Fourier transform but with the components spread out to higher frequencies. And the power spectrum looks like this.

And notice that one more final point here is that when you look at power spectra, often signals can have frequency components that are very small so that it's hard to see them on a linear scale. And so we actually plot them in this method. You plot them in units of decibels. And I'll explain what those are the next time. But that's another representation of the power spectrum of a signal.

OK, so that's what we've covered. And we're going to continue with the game plan next time.