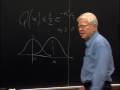Lecture 23: Detection for Flat Rayleigh Fading and Incoherent Channels

• Download English-US transcript (PDF)

The following content is provided under a Create Commons license. Your support will help MIT OpenCourseWare continue to offer high quality education resources for free. To make a donation or to view additional materials from hundreds of MIT courses, visit MIT OpenCourseWare at ocw.mit.edu.

PROFESSOR: Let's get started then. We went through Rayleigh fading very, very quickly last time. I want to spend a little more time on it today since it's one of the sort of classical models of wireless channels. And it's good to understand how it works. And it's good to also understand what all the assumptions that are made when one assumes Rayleigh fading, because they're really quite a few of them. OK, so what we're doing is we're assuming flat fading. In other words when we talk about flat fading, we're talking about fading where if you generate a discrete model for the channel, that discrete model is just going to have one path in it. In other words, the output is going to look like a faded version of the input. It'll be shifted in phase because of the unknown phase in the channel. It'll be attenuated by some random amount. But if you look at the waveform, it'll look like the waveform that you transmitted except for the noise. And that's what really is represented by this one tap model that we've been looking at.

In general we've said that you can model a pretty arbitrary channel for purposes of somewhat narrow band communication by using a sequence of taps where usually for want of something better to do, we model those taps as being Gaussian random variables, complex Gaussian random variables with zero mean, and variables which are circularly symmetric. And we assume for not any very good reason, that the taps are independent of each other. I mean we have to make some assumptions or we can't start to make any progress on trying to analyze these channels. But we should realize that all of these assumptions are subject to a certain amount of question.

OK. When we assume a single tap model, and these tap models are always given with the number of the tap given first, and the time given second. So what we're assuming here is the only tap is the tap at time 0. And it's at time 0 because we're assuming the receiver timing is locked at transmitter timing. And we're just going to get rid of the zero because there's only one tap, and call this G sub m. We're also going to pretty much assume that G sub m stays relatively constant for a relatively long amount of time. Except as far as this analysis of Rayleigh fading goes, we don't have to assume that. Because in fact, when we're assuming Rayleigh fading, the analysis that we're going to follow, the receiver doesn't know anything about the channel at all, except that it's a single tap model. And therefore what the receiver does is it goes through maximum likelihood detection assuming that that single tap is just a complex Gaussian random variable.

OK when you have a complex Gaussian random variable as you've seen in the problem sets and we've noted a number of times, the energy in that complex Gaussian random variable is exponential. And the magnitude is just a square root of the magnitude squared, namely the energy. And that has a Rayleigh distribution which looks like this, namely the probability density of how much response you get. We'll base this law here. And the phase of course, is equally likely to be anything. Namely the phase is uniform and random. This density looks like this. I wanted to draw this so it would emphasize the fact that the magnitude is in fact, always nonnegative. But also to emphasize the fact there's a whole lot of probability down here where there's very, very little channel. And this is in fact what gives rise to the fact that if you try to communicate over Rayleigh fading, and you don't make any use of diversity-- and we'll talk later about diversity-- in fact you can't communicate very well at all. And that's because of this very bad region here where the channel is very badly faded. You send a bit on this channel which is very badly faded, and there's nothing much the receiver can do. And that's the thing we want to try to get a real feeling for.

OK so the output of the channel when you put in an input U sub m, and we'll think of this as being a binary digit for this time being. So the output is going to be the input times this tap variable, which is this complex Gaussian random variable plus a noise random variable, which we're also assuming is complex Gaussian and circularly symmetric. OK so what we have, if you're going to make two hypotheses about two possible values of U sub m, look at what this random phase does here. No matter what U sub m you transmit in one epoch of time, the channel is going to rotate this around by a completely random phase. It's going to add a noise to it which has a completely random phase. And the output is going to come out. And the output has a completely random phase. Namely the phase of the output cannot possibly tell you anything about what input you're putting into the channel. OK so in other words, in this model that we're using, the phase is completely useless. And if we want to talk about anything connected to using likelihoods, the only thing we can use is the magnitude of the output. OK.

Now, why don't we just analyze it in terms of the magnitude of the output? Well when you analyze these problems, Gaussian things are usually much easier to analyze than things like this. Not always, I mean we have to get used to analyzing all of them. But this particular problem of Rayleigh fading is really easier to analyze in terms of these Gaussian random variables. But it's easier to understand in terms of recognizing that the only thing you can make any use is these magnitudes.

OK if we only use one complex degree of freedom in a signal, namely if we try to send some signal and we only use one input to the channel, then we only get one output. Namely we sent U sub 0, we get V sub 0. And we try to decide from V sub 0 what was sent. We're really in a very bad pickle at that point. Because the only thing that makes any sense, since we can only use the magnitudes, is to send a very small magnitude or a positive magnitude. Magnitudes are positive anyway. So if you're going to send binary signals, this is your only choice-- if it makes any sense-- if you make this larger than zero you're just wasting energy. So you only have this choice. And you can choose the amplitude a that you're using. But that's the only thing that you can do.

OK, this is a very nasty thing to analyze for one thing. It gives you a very large error probability for another thing. Nobody uses it for another thing. And therefore almost all systems of trying to transmit in this kind of Rayleigh fading, always use at least two sample values. In other words, instead of just putting one complex degree of freedom into the channel, you're going to put two complex degrees of freedom into the channel. And the thing that we're going to analyze, because it's the easiest thing to do in this discrete time model we've developed, is to think of modeling hypothesis 0 as sending two symbols U sub 0 and U sub 1 will make U sub 0 equal to a, and U sub 1 equal to 0. And the alternative case, if we're going to try to send input 1, this is binary transmission. You can talk about more than binary transmission, but binary is awful enough. You get U sub 0 and U sub 1 is equal to 0 and a. So what you're going to be doing here in this pulse-position modulation, is choosing one of these two different epochs to put the data in. So in one case, you put all your energy in the first one. In the other case, you put all your energy in the second one. Mathematically, this is completely equivalent to frequency-shift keying, that's completely equivalent to phase-shift keying. And if we had a little more time, we could talk about that. And I'll probably put an appendix in which talks about those two systems. But in fact, it's completely the same thing. It's just that you're using different complex degrees of freedom than we're using here. So we're really analyzing FSK and PSK. And that's where people usually come up with these analyses of Rayleigh fading.

OK when we have input 0, what we receive then, is the 0 is going to be the input a, times the magnitude of the channel of time 0, plus a noise variable. The noise is complex Gaussian, remember. The second input is just going to be the noise variable. Alternatively, if we're sending the second symbol, which means we put our energy into the second degree of freedom, it means that what we're going to get is the 0 was just going to be the noise. And the second output is going to be the signal plus the noise. And remember, both this variable and this variable are both complex Gaussian. The phase doesn't mean anything. So what we can use is simply the magnitude.

OK, so when we have hypothesis equal to 0, what comes out is going to be, the 0 is going to be a complex Gaussian random variable. Let me introduce a new piece of notation now. Because it gets to be a real mess to constantly talk about a Gaussian complex random variable, and talk about it's real part and imaginary part as being independent Gaussian. So I'll just call this normal complex. And this first thing is the mean, which is a real and imaginary part, but it's zero in most of the things we deal with. And the second one is the mean square value of this random variable V sub zero. So this quantity here is now twice the variance of the real part of V sub 0, and twice the imaginary part of the variance of v0.

We scaled the noise in a peculiar way here. And I apologize for all of the mess that occurs when we do this. Because sometimes we think of the noise as having variance N sub 0 over 2 in each real and imaginary degree of freedom. And therefore N sub 0 in a complex degree of freedom. And sometimes we think of it as having variance N sub 0 W Where does that difference come from? It's this infernal problem of the sampling theorem being so critical in most of the models that we talk about. OK because when you use the sampling theorem, the sinc x over x waveforms that we use are not orthonormal, they're orthogonal. And this factor of W appears exactly because of that. They appear because the magnitude of the signal is a, and the energy and the power in the signal is then a-squared. OK. In this case the power in the signal is not quite a-squared because we only send energy in one or the other of alternate degrees of freedom. So therefore, if we look at a time one second, we get W complex degrees of freedom to use. We only send energy in half of those so that the actual power that we're sending is a-squared divided by 2.

OK. Because of that, when we normalize the noise the same way the signal is normalized, we get this variance W N sub 0. If you're confused by that, everyone is confused by it. Everyone I know, when they go through calculations like this, they always start out with some arbitrary fudge factor like this. And after they get all done, they think it through or more likely they look it up in a book to see what somebody else has gotten. And then they sweat about it a little bit, and they finally decide what it ought to be. And that's just the way it is. It's the problem of having both the sampling theorem and orthonormal waveforms sitting around. It's also the problem of multiplying the power by 2 as soon as we go to passband. Because both of those things together generate all of this difficulty.

But anyway, this is the way it is. And the important thing for us is that what we can have now is under these two hypotheses. We just have two Gaussian random variables, complex Gaussian random variables. And in one case, the larger mean square value is in one. And in the other case the larger mean square value is in the other.

OK. So just reviewing that. If H is equal to zero, V sub 0 and V sub 1 are these complex Gaussian random variables. If H is equal to one, then we have this set of Gaussian random variables. The probability density of V sub 0 and V sub 1, and now it's more convenient to use the real and imaginary parts for the Gaussian density. Anytime you're working problems of this type, try both densities using real and imaginary parts, and using magnitude in phase, and see which one is easier. Here it turns out that the easiest thing is just to use the ordinary conventional density over real and imaginary parts. And what we wind up with is this Gaussian density. On V sub 0 the density is V sub 0 squared divided by the variance a-squared plus W N sub 0. And on V sub 1, it's this Gaussian density V sub 1 squared divided by W N sub 0. Just because here we have this variance. Here we have this variance. OK, on the alternative hypothesis when H is equal to one, you have the same thing but the denominators are switched around. When you take the likelihood ratio, you want to take the ratio of this, to the ratio of this. If you look at it and you take the logarithm of that, you're taking the ratio of this to this. Incidentally the coefficient here, you could write it out if you want to. It's 1 over the square root of blah, times 1 over the square root of blah. But if you recognize that the coefficient here has to be the same as the coefficient here, you don't have to worry about it.

So when you take the log likelihood ratio, you get this divided by this. You have the same form in both cases. In one case, you have this term minus this term and this term minus this term. And the other case well, for V sub 0, you have this term minus this term. And for V sub 1 you have this term minus this term. Because of the symmetry between the two, this just comes out to V sub 0 squared minus V sub 1 squared times a-squared. And when you do the algebra, the denominator is a-squared plus W N sub 0 times W N sub 0.

OK. What do we do for making a maximum likelihood decision? Maximum likelihood is map when the threshold is equal to 1, which is when the logarithm of the correct threshold is equal 0. Which says that you take this quantity, and if it's nonnegative, you choose H equals zero. And if it's negative, you choose H equals one. Which says you compare V sub 0 squared and V sub 1 squared. And whichever one is larger, that's the one you choose. And if you go back and look at the problem, it's pretty obvious that that's what you want to do anyway. I mean you'd be very, very surprised when you're comparing two Gaussian random variables where one of them has a larger variance than the other. And on the other hypothesis, the absolon has the larger variance. If you came up with any rule other than to take the magnitude squares and to then compare those two magnitude squares, you would go back and look at the problem again realizing you must have done something wrong.

But anyway when you deal with problems like this, I advise you to take log likelihood ratio anyway. Because every once in awhile you find something which comes out in a somewhat peculiar way. But anyway, here there's nothing peculiar. So what we have to do now is to find the probability of error. Now what's the probability of error? OK if we actually transmit zero, then V sub 0 squared is exponential. It's exponential with this mean. Namely this is the mean of V sub 0 squared. And V sub 1 is exponential with this mean. In other words, this is a big exponential. And this is a little exponential. The two of them have probability densities that look like this. This is not going to work. The big one has a probability density that looks like this. And the little one-- this is big-- and the little one has a probability density that looks like this. And what you want to do is to subtract a random variable with this density from a random variable with this density. So you're convolving two exponential densities with each other. And unfortunately, you're taking the differences of two. So you're convolving the negatives of this with this. And then you have to integrate the thing. And it's just something you have to do. And the answer is, the probability of error is then 2 plus a-squared over W N sub 0 to the minus 1.

OK that is really an awful result. Because that says that if you increase the energy that you're using, the probability of error goes down very, very, very slowly. And if you look at this picture you think about it a little bit, it should be clear that that's the only thing that can happen. OK. Because if you increase a-squared a little bit, it's not going to save you much here. Because when you have a bigger a-squared, it's just going to move down the value of g bar that's going to give you trouble. Namely when you double a, the value of magnitude of g that gives you trouble just goes down by a factor of two. When that goes down by a factor two, this bad part of the curve just goes down in a quadratic way. Well that's what this is telling us. OK. I mean the thing that we see is a quadratic and a. So we're sort of assured that we're doing the right thing. And we're sort of also assured that the reason why this result is so awful, is just that sometimes the fading is so bad there's nothing you can do about it.

OK now the signal power as we said before is a-squared over 2. Since half the inputs are zero. So we can put twice as much energy into the ones that are non-zero. And therefore when you put this in terms of the average signal energy that you're sending, what we get is E sub b over N sub 0. OK. So that again says exactly the same thing that this does. It's worthwhile keeping both of these notions around, because we have done something kind of peculiar here. I should mention it for you. As soon as you're looking at a fading channel, the power that you're talking about becomes a little peculiar. Because remember when we were looking at white noise channels? What we were looking at is the power at the receiver, the signal power as received at the receiver.

Now at this point, we still want to talk about E sub b. We still want to isolate this problem from the attenuation that occurs just because of distance and things like. Because of that, when we model g, this original model that we use here was a model in which the magnitude of g had mean one. And we made it have mean one so that the energy would come out right. Which is another reason why you get confused with these E sub b over N sub 0 terms. OK so anyway, that's the answer. And E sub b is in terms of the received energy using the average value of fading.

OK we next want to look at non-coherent detection. Non-coherent detection is another thing that communication engineers use all the time, talk about all the time. And you have to understand what the difference is between coherent transmission and incoherent transmission. The general idea is that when you're doing incoherent detection, you're assuming that you don't know what the phase of the channel is. And somehow you want to do your detection without knowing that phase. The difference between Rayleigh fading on this kind of channel and incoherent detection, is that with incoherent detection the receiver is assumed to know what the magnitude of the channel is, but not the phase. It's harder to measure the phase of the channel than it is the measure of the magnitude. Because the phase changes very, very fast. If you look at these equations we have for what the response of the channel is, you see the phase changing many, many times during the time where the amplitude of the fading changes by just a little bit.

So a very common assumption that people make when trying to do detection is that it's incoherent. Partly, people get used to analyzing incoherent communication. And I've seen this so many times. And they insist on building communication systems using incoherent detection. They will swear up and down there's no way you can measure the phase. And what they're really saying is that's the only kind of communication they understand. And because that's the only thing they understand, they become very, very upset if anyone suggests that you ought to try to measure the phase. But that's a tale for another day.

OK so now we want to look at the case where we're assuming that we know the magnitude of the channel. It's just some quantity that we'll call g tilde. We're assuming that the same magnitude occurs both on U sub 0 and U sub 1. We're going to use the same transmission system that we used before, namely pulse-position modulation. We'll either put our energy in U sub 0 or we'll put our energy in U sub 1. We'll try to detect what's going on. But we just give the detector this little extra amount of ability of knowing what the channel is. I'm going to talk more later about how you can use this knowledge of what the channel is, and how you can measure what the channel is. But for now we just assume that we know it. So the phase is random and independent of everything else. So under hypothesis H equals zero, we have the output of the channel. And times 0 is whatever input level we put in a, times what the channel does to us, times e to this random phase. And V sub 1 it's just-- plus Z sub 0. And in the other case we have V sub 1 equals Z sub 1. And under the other hypothesis V sub 1 is this input with a random phase but a known magnitude and again, a Gaussian random variable.

Phases are independent of the hypothesis. The phases are independent of the magnitudes which are known. The phases are independent of everything and therefore, we just want to forget about them. So the question is, how do we make a maximum likelihood decision on this problem? Well you look at the problem. And for the same reason as before you say, it's obvious how to make a maximum likelihood decision just from all the symmetry that you have. If the magnitude of V sub 0 is bigger than the magnitude of V sub 1, V sub 0 corresponds to this little bit of extra energy that you have. So if V sub 0, the magnitude of V sub 0 is positive, is bigger than the magnitude of V sub 1, you want to choose H equals 0. And alternatively you'll want to choose H equals 1. It's obvious right?

I've tried for years to find a way to prove that. And the only way I can prove it is by going into Bessel functions which is the way that everybody else proves it. And this seems like absolute foolishness to me. And if any of you can find a way to do this, I would be delighted to hear it. I will be in great admiration of you. Because I'm sure there has to be an easy way to look at this problem. And I just can't find it.

OK anyway, we're not going to worry about all these Bessel functions, because that's just arithmetic in a sense. So we're just going to say well it can be proven using all of this machinery. So what we really want to find is what is the probability of error when we make that decision. And when we make that decision, namely what we're looking for is the probability of this magnitude then, is bigger than this magnitude when H equals one is the correct hypothesis. Because that's the probability of error then. So you have these two different terms. You just go through all of the junk that's in the appendix to the notes we passed out last time. If you want to go through that, I think it's great. It's an interesting analysis. Certainly not going to do it now.

When you get done doing that you find out the probability of error is exactly one half times e to the minus a-squared times this known magnitude of the channel. I mean, a-squared and g tilde have to appear together here. OK because what's coming out of the channel, the magnitude of what's coming out of the channel without noise is just a times g tilde. They both come together everywhere. And therefore, they have to come together anytime you're talking about optimal detection, probability of error, or anything else. So these two appear together. We have the same noise term down here as we had before. Because again we're using a sampling theorem analysis and the noise in each of these random variables is W N sub 0.

OK so that's a little surprising that that's what the noise is. If you knew the phase also, if the detector knew both the magnitude and the phase of the channel, it would be the conventional Gaussian problem that we've analyzed many times before. And the solution would be that probability of error is equal to Q of a-squared times g tilde squared divided by W N sub 0. Now if you remember the estimates we've come up with and the bounds we've come up with on the Q function, the simplest bound that we came up with was this. Namely you take this thing, you take one half of it, which is the Gaussian density with the coefficient. You multiply it by one half. So this is the simplest estimate we can get of this. On the other hand when this quantity is large, a much better estimate of this is to have that estimate which has a 1 over the square root of pi times W N sub 0 over a-squared g tilde squared in it. So we have that term extra. Which says that when this is large, whenever we're communicating at all reasonably, this probability of error is much smaller than this probability of error.

However you talk to any communication engineer, and they'll say when you have a good signal noise ratio, incoherent detection is virtually as good as coherent detection. And why did they say that? Well it's because the probability of error goes down so quickly with energy here. It's going down as a square of an exponent. Well it's going down as an exponent in the energy. The question you want to ask is how much extra energy do I have to use? If I'm using coherent detection, how much more energy does an incoherent detector need at the input in order to get the same results? And then you see the question is very different. Because if I increase this quantity just a little bit, this probability of error goes down like a bat. OK. So what happens then, when you compare these two terms is that as the signal to noise ratio gets larger and larger, the amount of extra energy you need to make incoherent detection work as well as coherent detection goes down with 1 over a-squared.

Which says that these communication engineers who swear that they like incoherent detection in fact, have something on their side. because they don't have to assume so much about the channel. They have something which is more robust. And in fact what's turning out here, is that even though this error probability is a little bigger than this error probability, there's only a very negligible amount of extra dB required to make the two the same. So it only costs a little bit of extra energy to be able to use incoherent detection instead of coherent detection.

OK so this is very strange now. We have a nice error probability which is almost as good as the Gaussian error probability using incoherent detection. This is assuming that the channel, that the receiver knows what g tilde is. But now we go back and think about this, and look at our detection rule, which is the optimal detection rule. And the optimal detection rule is no matter what g tilde happens to be, we compare the magnitude of V sub 0 with the magnitude of V sub 1. In other words, we have analyzed this assuming that we know what g tilde is. We know what the gain of the channel is. But the receiver doesn't pay any attention to it. OK so now we have this very peculiar situation where incoherent detection with a known value channel is almost as good as coherent detection is.

But at the same time Rayleigh fading gives this awful error probability. So now you have the final part of the argument take this probability of error, multiply it by the probability density of g tilde squared, integrate it to find out what the average error probability is when we average over the channel fading. And guess what answer you get? Well you ought to be able to guess it if you've looked at the homework already. Because in the homework you actually go through this integration. And bingo you get the Rayleigh fading result. Which says that the problem with Rayleigh fading is not any lack of knowledge about the channel. Knowing what the channel is would not give you, even knowing what the phase is of the channel would not give you a lot of extra help. The only help in knowing what the phase is, is to get this result instead of this result. And even that won't help you much. The problem is anytime you're dealing with Rayleigh fading, the channel has faded so badly a large fraction of the time, that you can't get an acceptable probability of error.

OK so now we have to stop and think. What do you do about this? Well you have two general kinds of techniques to use at this point. OK and one of them is to try to measure the channel at the receiver. You take the measurement of the channel at the receiver. You send it to the transmitter. And the transmitter then does something to compensate for the amount of fading. One thing that the transmitter can do is anytime the channel is badly faded, it increases the amount of power that it's sending. That's what typical voice systems do. And the other thing that you can do is change the rate at which you're transmitting. You can do all sorts of things with the transmitter if you know what the channel is. You can respond to it in various ways. And all these different communication systems have various ways of dealing with that. And we'll talk a little about that on Wednesday when we talk about CDMA.

The other thing you can do about it is use something called diversity. And the idea of diversity is that instead of sending this one bit, trying to use as few degrees of freedom as possible, you try to send your bits using as many degrees of freedom as possible. If you can use a large number of degrees of freedom, and if the fading is independent on these different degrees of freedom, then in fact you gain something. Because instead of having one random variable which can totally cripple you, you have lots of random variables. And if any one of them is good, you get through. So you get a benefit out of diversity.

OK so that's our next topic. Namely, how do you measure the channel? Because if you're going to use diversity it's a help to know the channel. If you're going to use coding, coding is just another way to get diversity. Again your coding will work better if you know what the channel is. So somehow we would like to be able to measure the channel and send it back to the transmitter if we want to alter the power, the rate of the transmitter, and to let the receiver use it if the receiver is going to. Well we have seen that when you use one bit on just a couple of degrees of freedom, knowing what the channel is does not do you much help. If you use coding or if you use one bit and spread it over a large number of degrees of freedom, then knowing what the channel is gives you a great deal.

This is one of the basic confusions that everyone has when they deal with Rayleigh fading. Because when you look at a Rayleigh faded channel, the first thing you analyze is this incredibly small number of degrees of freedom. And you say wow, that's awful. There's no way to deal with that. And then you start looking for something. And you say, well diversity helps me. But in general, this is the general scheme of things that we're going to use.

OK. So as we said channel measurement helps if diversity is available. Why does that help when diversity is available? OK, think of sending this one bit. You get one reception, and then you get another reception. And on this reception, you get one amount of fading. On this reception you get another amount of fading. If I don't know how much fading there is it doesn't help me an awful lot. It helps me some. But if I know that this channel is faded badly and this channel is not faded, then I'm going to use what comes out here instead of what comes out here. And then my detector is going to work much, much better. When you look at diversity results, always ask yourself a couple of questions. Is the detector using knowledge of what the strength of the channel is on these two diversity outputs? Is the transmitter using it's knowledge of what those channels are? You get very different results for diversity depending on the answers to both of those questions.

OK, so if you have a multi-tap model for a channel-- OK remember the multi-tap models that we came up with. We we're looking at transmission using multipath. And we had multipath in different ranges of a delay. We came up with a model which gave us multiple taps for a discrete model of the channel. You get a large number of taps if you're using broadband communication. Because using broadband communication 1 over W becomes very small. And therefore these ranges of delay become very small. And if you're using very narrow band communication, that's when you have the flat fading. Namely flat fading is not flat fading, it's fading which is flat over the bandwidth that you're using. So if you use a broader bandwidth and you have multiple taps, then these taps are going to be independent of each other. And you automatically have diversity.

So the question is how do you use that. Well if you're going to use it, you better be able to measure it. OK so now we're going to try to figure out how to do that measurement. And the first thing to do is to assume the simplest possible thing. I mean, suppose you know how many taps the channel has. Suppose it has k sub 0 channel taps. So the channel looks like this, G sub 0, G sub 1, and G sub 2. You're transmitting a sequence of inputs. OK remember all of this stuff came from trying to model a channel in terms of discrete inputs, where you're sending one input each one over W seconds. So you put in a sequence of inputs. You have these three different channel taps here. And what comes out when you put in a single bit here or a single symbol. You get something out when this tap right away. You get something out here one time unit later. You get something out here, one epoch still later.

So all of these outputs get added up. And therefore the output here at time m, is the input at time m times this tap, plus the input at time m minus 1 times this tap, plus the input at time m minus 2 times this tap. Because it takes these inputs that long to go through there. All this is is just digital convolution, OK. I'm just drawing it out in the figure so you see what's going on. Because otherwise you tend to think everything happens at one instant of time. Then we're adding this white Gaussian noise. When we're talking about digital systems, white Gaussian noise just means that each of these random variables are independent at each other random variable. They all have the same variance. And the real parts and imaginary parts have the same variance. And they're independent of each other. Namely these are all normal random variables. Since we're sending a, or minus a, or something with magnitude a, we want to divide by a out here, if we want to figure out anything about what these taps are.

OK so suppose that what we send now is a bunch of zeros, followed by a single input, followed by a bunch of zeros. What comes out? Well the thing that comes out is at the point that this big input comes in, we get a G sub 0 out at the time that you put in a. I mean we're leaving out propagation delay here. We got a times G sub 1, the next epoch. Then we get a times G sub 2, the next epoch. And by that time the input is completely out of the filter. And we get zeros after that. So if you put in a bunch of zeros and then a single a, you got a nice measurement of the channel. There's Gaussian noise added to each of these inputs. But in fact you do get a reading of each channel output. When you divide these by the a here, then you get something which is a measurement of the appropriate tap G plus Gaussian noise on it.

OK now you try to make an estimation from this. And the trouble is we don't want to say much about estimation theory. But in fact the notes gives you a very brief introduction into estimation. There are two well-known kinds of estimation. One of them is maximum likelihood estimation. And the other one is minimum mean square error estimation. Maximum likelihood estimation is in fact exactly the same as maximum likelihood detection. Namely you look at the likelihoods which is the probabilities of the outputs given the inputs. And what's the input in this problem? The input is these channel variables. Because that's the thing we're trying to measure in this measurement problem. We assume that the probing signal is known. It's just a bunch of zeros, followed by a, followed by a bunch of zeros. So we know that. We're trying to estimate these things.

So these are the variables that we're trying to estimate. So we try to find the probability density of the output conditional on the knowledge of G sub 0. Which is just the Gaussian density shifted to a times G sub 0. You then look at the maximum likelihood estimate of G. So you're looking at the value you can put in to maximize this estimate which comes out here as a times G sub 2. And then at this appropriate time, you're looking at G sub 2 here, plus a noise random variable. And since the noise is zero mean, this quantity here is in fact the best estimate in terms of the maximum likelihood that you can get. If you assume that this is a Gaussian random variable and this is a Gaussian random variable, you can solve a minimum mean square error estimation problem. It's much like the map problem except these random variables are all continuous here. But it's a little different from the map problem in the sense that you can't have equally likely inputs where you have a continuous random variable. You make them all equally probable. The only possible value you can have is zero. Because it has to extend forever. So anyway, maximum likelihood detection is just normalize what you get so that in the absence of Gaussian noise, you would get the variable you're looking for. And then ignore the Gaussian noise, and that's your estimate.

OK. If you want to do this and you want to use the strategy, it looks like a very nice strategy. But what's the problem in it? If this sequence is somewhat longer, you need a whole lot of zeros in between each probing signal. And what that means is you're going to be using your energy and clumping it all up into the small number of degrees of freedom. Which means you're going to be sending a lot of energy at one instant of time and then nothing for a long period of time, then a very big signal for awhile then nothing for a long period of time, and so forth. If you do that, the FTC is really going to be down on you. Because you're not supposed to send too much energy in any small amount of time or any small amount of frequency. So you're supposed to spread things out a little bit. You say OK, that doesn't work too well. What am I going to do? How can I choose a sequence of input so they have relatively constant amplitude, but at the same time so that when I go through this kind of filter, I can sort out what's coming from here, and what's coming from here, and what's coming from here. Well it turns out that the answer to that question is to use a pseudonoise sequence. And the next thing I want to do is to give you some idea about why these pseudonoise sequences work.

OK so we'll think in terms of vectors now. OK so we have a vector input, u sub 1, u sub 2, up to u sub n, a vector of length n. So we're putting these discrete signals in one after the other. We're passing them through this, which is a digital filter now. So what comes out here V prime is just a convolution of u and G. We then add the noise to it. I claim that what we ought to do is use the matched filter here to u. And if I use a matched filter to u here, that matched filter, if I'm using a pseudonoise sequence, is going to bingo give me the filter that I started out with, plus some noise.

OK why is that? The property that pseudonoise sequences have, if I choose each of the inputs to have the magnitude of a, and think of it as being real plus or minus a, which is what people usually do. If you look at the correlation of this sequence, namely the correlation of u sub m with the complex conjugate of u sub m spaced a little bit, PN sequences have the property that this correlation function looks like an impulse. OK. Now how you find sequences that have that property is another question. But in fact they do exist. There are lots of them. They're easy to find. And they have this very nice property.

Another way to say this is that is that the vector u has to be orthogonal to all of its shifts. That's exactly what this is saying. And another way of saying it is that u, if you pass it through the matched filter to u-- now remember what a matched filter is on an analog waveform. You take a waveform, you switch it around in time. You take the complex conjugate of it, and that's the matched filter. And when you convolve u with this matched filter, what it's doing is just exactly the same operation of correlation. OK in other words, convolution with one of the sequences turned around this time, is the same as correlation. And most of you have seen that I'm sure.

So that if we take this matched filter where u tilde sub j is equal to the complex conjugate of u at time minus j, then I pass u through the filter G. Forget about the noise for the time being. I then pass it through the matched filter u tilde. What I'm going to get out, I claim, is G. And I'll show you why that is in just a minute. Let make caution you about something. Because you can get very confused with this picture. Because as soon as I take this input, u 1 up to u sub m. This matched filter is going to start responding at time u sub minus m. And it's going to finish responding a time u sub minus 1. So it responds before it's hit. Which again is this business of thinking of timing at the receiver being very much delayed from timing at the transmitter. Which is a trick that we've always played. Which is why we don't have to think of filters as being realizable. Still in this example, this becomes confusing. And I'll show you why in a minute.

OK so I'm going to assume that I picked a good PN sequence. So when I convolve it with its matched filter I essentially get an impulse function, namely a discrete impulse. Which is the same as saying that u is orthogonal to all of its shifts. And that's exactly what you what to do. You want to think of turning it around and passing it through. And that's exactly what this is doing. OK so we have the output of this filter, which is u convolved with G. We're then convolving that with this matched filter u tilde. And now we use the nice property of convolution, which you probably don't think of very often. But the nice property that convolution has, is that it's both associative and commutative. OK. And therefore when we look at V prime times u tilde, it's the convolution of u with G-- that's what the prime is-- all convolved with the matched filter u. Because of the associativity and the commutativity, you can reverse these two things so you're taking the convolution of u with its matched filter. When you take the convolution of u with its matched filter, you get a delta function. And you take a delta function and pass it through G. And what comes out is a delta function weighted by a-squared n, which is just the energy of what we're putting in. OK so that says that if we can find pseudonoise sequences, all of this works. And it works just dandy. If you put noise in, what happens there? Well let's analyze the noise separately. The noise is going through this matched filter. Well if u is a pseudonoise sequence, if it has this nice correlation property and you flip it around in time, it's going to have the same nice correlation property. So that in fact u tilde is going to have the same property that it's orthogonal to all of its time shifts.