Flash and JavaScript are required for this feature.
Download the video from iTunes U or the Internet Archive.
Description: This lecture covers depth perception, including mechanisms used to analyze depth. The video includes discussions of these mechanisms such as the effects of lesions in V4 or MT regions and stereoblindness, motion parallax, shading and perspective and how depth is processed by cortical structures.
Instructor: Peter H Schiller

Lec 7: Depth perception
The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high quality educational resources for free. To make a donation or to view additional materials from hundreds of MIT courses, visit MIT OpenCourseWare at ocw.mit.edu.
PROFESSOR: All right, so today our topic is going to be depth perception, which, as I have mentioned to you before, is certainly one of the most intriguing achievements in vision. Because the impressions onto the retinal surface essentially two dimensional. And from that, somehow the brain needs to reconstruct the third dimension. And what is interesting about this also, that even in the most primitive animals, this is a must. And so annals with tiny brains also have mechanisms to be able to calculate depth from the information that comes in through their eyes.
And to demonstrate that, I have here a frog, which has a tiny little brain like that, has big eyes, and this frog, for its existence, needs to know exactly where things are in depth. Because if he doesn't, he would starve to death. And so what a frog does looks something like this, very crudely. He will stick out his tongue, grab a flying insect and consume it. And because of this incredible capability, it is a well-adjusted, healthy animal in most parts of the world.
Now the big question then comes up, how do we carry out these computations. What kind of mechanisms are involved in being able to compute where things are in space, either in absolute sense where it is from you and in a relative sense where one object is relative to another one. Now it turns out that this became such a serious problem, in the course of evolution, that actually several different mechanisms have evolved to make possible our ability to see things in depth.
And so when one looks at this as a list, as a fairly brief list, we can make a distinction between so called ocular motor cues and visual cues. The ocular motor cues are accommodation and vergence. So if various objects are at a very distance from you, your eyes converge or diverge. And you your lens gets thicker and thinner. And that information can be utilized in a rather crude way to tell you about where things are in that relative to you.
Now as far as visual cues are concerned, the very significant one we are going to talk about quite a bit, is a binocular cue, which is called stereopsis as you all know. And then we have a whole bunch of monocular cues motion parallax, shading, interposition, size, and perspective. And so we will talk about many of these to give you a sense of what it is like and to give you a sense of what various brain structures do with this as a result of extensive research that had been done in this area.
So now, first of all, let's talk about stereopsis. And we talk about stereopsis, we're going to talk about the basic facts of it, and then we are going to have some demonstrations. First of all, the so called stereoscope, of whichever modern version that has been handed out to you, the stereoscope was invented in the late 19th century. And when that was done, the initial approach to this was to be able to present to each eye separately an image that was taken by a camera that has two lenses, which are apart about as much as your two eyes are apart.
And each of those created a separate image of what's out there. And, of course, each eye gets a very slightly different perspective of what's there. And then when you present these two images that you had collected separately to each eye, you get a very strong sense of real depth, as you will see in just a minute. Now another way to do it, which nowadays is easier because you can barely ever find even one of these two-lens cameras, even in stores that sell ancient materials, antique stores.
So sometimes what you do instead, if you only want to take a picture of a static image, that you can take a camera, put in a track, and have it take two pictures in succession. And then you can do the same thing as you do with a serial camera. You can present one to each eye. OK, so, what we are going to do now, we are going to have a series of demos. And so we have a handout for each of you, the paper. And that you can keep and take home.
But the stereoscope that I have for each of you, that you're going to have to leave behind, because I need to use that in other classes. So what I want you to do then, there are two pictures on the first page that you put the stereoscope down onto the page so that the vertical line cuts it in half so that one goes into each eye. And then you put your head right down to it to look into it, all right?
And if you do that, if you have it properly sectioned, you're going to have a sense that that image is actually three dimensional. It's an ancient, ancient old picture on purpose. But you should still be able to see it in depth. So that's the initial thing. This became quite a parlor game and for that case, for many, many decades, whenever you went to a party, they would hand out to you a stereoscope, a handheld one, and they would show you all kinds of images.
And you can even do this today when you get on the internet to find such displays. Now, then a very important discovery was made. I shouldn't say discovery, really, I should say an invention was made by Bela Julesz who came up with a so-called random dot stereograms. By the way, don't look at the bottom one, that just tells you what it's going to look like. There's nothing to look at the bottom, the bottom set.
Now if you look in the middle set, that looks like a random dot stereogram. And the idea here was that the only cue that you provide is stereo cue, nothing else. It's pure. And so what can be done here, you can take a section here, or the same on each side, and simply move a few pixels, those images as a unit, over. And when you do that, they're going to stick out in depth. So now take you stereoscope and look in the middle display, and you look through it, you should see something sticking out in depth.
And the first question I'm going to ask you is how many of you can see something stick out in depth? What do you see? You see
AUDIENCE: A square.
PROFESSOR: A little square sticking out? All right, so now, don't try to look at the bottom one. That simply tells you what the procedure was in that center section where you see the square sticking out. The pixels were moved a few steps inward from both the left and to the right creating what is called a disparity. And that's what the brain then can calculate for depth.
So now to provide you with the acid test, go to the second page. Now you look at the second page, everybody see the letter on top? You don't even have to look through the stereoscope, obviously you see the letter E, right? That's because that section is made darker. But now if you do the same thing at the bottom, the only cue you have is the disparity cue. And the question comes up, what letter do you see there?
And let me just add, this can be used as a quick, general test. You can present these two subjects, and if it can present a whole bunch of different letters, and if they can see the letters, that means they can see stereo. If they cannot see the letters, then it looks like they may not see stereo. Now let me add one other fact here. As you move these progressively closer to each other like this, you increase the disparity. And that causes the image to be seen at increasing depths.
Our sensitivity is so great that when you look at this on a computer, a standard computer, if you move those images just one pixel from the left to the right, then from right to the left, you will see it in depth. And even monkeys can see as small step as one pixel. So now how many of you can tell me what was the letter at the bottom there?
AUDIENCE: H.
PROFESSOR: H, H, good. Anybody not being able to see the letter? Everybody sees it. Well, you guys are lucky. Because there are a significant number of people in the world who lack stereopsis, something like 5% to 10% of the population lacks stereopsis for a variety of reasons. We'll talk about that a bit more later. But one is sometimes you're born, and you're amblyopic in one eye. Sometimes you are strabismic, which means that your two eyes are not aligned, which in commonplace language is often called as being cross eyed or wall eyed.
Those types of people very seldom will have stereoscopic depth perception, even after it's corrected, especially if the correction is made by the time you're 8 or 10 years old, the correction won't help. It has to be done much, much earlier. All right, so that then is the very, very basics of the stereo procedures. And now another procedure that had been developed more recently is one which is called the auto stereogram.
So then if you go to the next page, and what you want to do is you want to look at this horizontally like that with the T on top. And then just look at it at sort of, I don't know, maybe about 20 inches from you, normal reading length. And what you want to do is to look beyond it. So stare beyond it. And if you keep doing that for a while, you will suddenly see an image, a three-dimensional image, as this comes actually from a book called The Magic Eye. There are several magic eye books in which all kinds of displays are done using these auto stereograms.
Does everybody see-- who can see what's sticking out? OK, what do you see?
AUDIENCE: Was it a shark?
PROFESSOR: You see a shark? OK. Now let me see if any of you don't see it. Keep staring at it. Look beyond it. Another thing that helps, if you look at it, bring it a little closer to you so you can look beyond it easier, gradually move it back and forth. And if you're patient, eventually you may be able to do this. The reason this is difficult is because you have to uncouple the vergence in your two eyes. You have to look beyond it slightly.
And, in fact, that is one of the reasons why testing people for stereopsis, an auto stereogram is not a very good procedure. Whereas virtually everybody can use a stereoscope without any trouble.
AUDIENCE: That's so cool.
PROFESSOR: Did you get it finally?
AUDIENCE: Yeah, that's so cool.
PROFESSOR: Yeah, all right so, if anybody is really interested in this auto stereograms is I say go to the store, the bookstore, and get one of those magic eye books. They're just a lot of fun. And you can just leaf through it. You don't even have to buy the book, just look through it at the store. And you'll see one interesting, clever image after the next. All right, so that's the stereoscope. And now let me explain to, I think I've mentioned this briefly before, the principles involved behind being able to see stereoscopic depth perception.
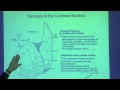
And what I've mentioned to you before was that if you have the two eyes fixating at a particular distance, if you then draw a circle around that, that's sometimes called a Veith-Muller circle, or the sometimes called a horopter, then any target, like this one here, will hit equivalent points on the retinal surface of the left and right eyes. However, if you do the same thing, and you put a target either beyond or closer than the Vieth-Muller circle, then they're going to hit nonequivalent points on the retinal surface.
So then by nonequivalency, we can do this and calculate this as to where the image falls relative to the central fixation spot in the foveola. And so then, when these nonequivalent points are hit, somehow the brain can measure this nonequivalence. And that is then converted into an estimate of where things are in depth. Now the idea behind this was that these nonequivalent points, that you have on the retinal surface, can connect in the cortex to single cells.
So they have a cell in the cortex that is binocular, by virtue of the fact that inputs from the left and right eyes. But they don't necessarily have to come from equivalent points. They can come from nonequivalent points. And that may be then the mechanism whereby it can tell you the degree of nonequivalence, and, therefore, convert that into depth. And, therefore, there could be single neurons in the brain that are selective to certain depths.
And so people began to do all kinds of experiments with this. And the way these experiments were done is you presented images separately to the left eyes and right eyes. And you could then present them to both eyes at the same time and vary the amount of disparity systematically to see what kind of tuning function you would get in the cortex. So this, some of the most beautiful work of this was done by a person called John [? Porgio ?] And I will tell you briefly about some of his experiments.
So here we go with then. We're going to look at the neural responses, neural responses in V1 as initially done in the monkey. So here's an example of a cell. We have here different degrees of disparity. And we have the neuron responding each time they're four repeated trials. And you can see the action potentials by these dark lines here. And what you do is you move the stimuli back and forth across the two eyes, the way it's actually done, you have a mirror. And then you have two in this experiment. You have two monitors, one to the left and one to the right. And then you can set it up almost exactly the same as what you would do with a stereoscope.
So this particular cell, as you can readily see, responds best when there's zero disparity. Now by contrast, here is a cell that responds vigorously at the far disparity and not to the close one. So then, when you do this, you can study hundreds of cells to see what kinds of distributions you have in the cortex for different degrees of disparity, cell activity. Now again, this hearkens back to what I talked about with respect to color vision where the question came up, if you want to see color, how many receptors would you need that peak at different wavelengths, right?
And one idea was that maybe you need as many photo receptors as there are colors. But in the end, it turned out that we have only three of them. And on the basis of that, we can recreate all the colors out there. Now the same thing applies to stereopsis. So when this was done systematically, here's an example of the tuning functions. This one here is the same, very much the same, as the first figure I showed you.
And so we have a bunch of different ones. And if you then study, as I've said hundreds of cells, you can come up with a distribution of this. And what John [? Porgio ?] came up with, he thought that there were four major classes. And the relative amount of activity of these four major classes then is used to compute all the very fine differences in depth. So there's a right on one. This cell is right on the fixation spot. And then you have near and far cells. And you have some in between cells.
Initially he thought there were four classes. Some people argue that there may be as many as six. But at any rate, there's a limited number on the basis of which you can calculate almost an unlimited number of depths, which is quite remarkable. All right, so now, what you can next turn to is to ask the question to what degree do various extrastriate areas contribute to stereoscopic depth perception.
And some people thought that this is a unique function for area MT, some people argue that maybe it's area V4, and so experiments were done in which it was examined to what degree stereoscopic depth deception is altered when you eliminate, say, area MT or you eliminate area V4. So that is what's been done. And you can think about it for a minute and say, well, what do you think? What do you think would happen in a monkey once you no longer had area V4? What you think would happen if the monkey no longer had area MT?
Well, the results were actually quite surprising. And they're shown here, same experiment as before. The Bela Julesz random dot stereograms. And then you're presenting one of four locations of however many little area where, like little square, that's sticks out in depth and you vary the amount of depth that sticks out by varying the number of pixels you moved the images into this place. And when that was done systematically, this is what was found. It was found that neither V4 lesion nor an MT lesion cause a significant deficit.
The only deficit that was significant had to do with a response latency. And as I should have mentioned earlier, like when we talked about the frog, one of the very important things about processing depth, again, is to be able to do it quickly. So when you have that's frog and the fly is flying along, he has to be very quick to compute it so that he can catch it, right, as you had seen. So in this case, what you see here, that there is about a 20 millisecond difference after V4 lesion, increase in latency, and quite a bit more, almost 40, 30, 40 after and MT lesion.
So that contributes to some aspect of depth processing in terms of being able to do it quickly. But neither the MT or V4 are unique in processing stereopsis. It looks like that it is processed in several different areas in the brain and inspire conjoint computation that you can arrive at the actual depth. And it's by virtue of that joint computation that you can do this very quickly.
So now you come to the next important depth cue, which is called motion parallax. This one is a capacity that we had acquired in the course of evolution, which is extremely potent and powerful. And it's based on a very simple physical fact. And the physical fact it that either when you are in motion, or something in the environment is in motion, the rate at which these images travel across the retinal surface is heavily distance dependent.
And so let me demonstrate this concretely for you. Here we have an eye that's fixed. It's always looking straight ahead. And we have two rods here, sorry, just one rod, that we are going to move into position gradually from here to here, and then back up as shown by the arrows here. And we examine the range over which these near and far and middle objects move across the retinal surface when you engage in this motion and the eye is stable.
And you can see that the far object moves over a much shorter distance than the near object. This you can readily do it yourself in an experiment. You can stick out your thumb and move your head back and forth. And you see that your thumb will move a lot more than the object that you're looking at.
So now the same thing also applies when you actually are engaged in the eye movements, which of course you do all the time. In this case, they eye is set up so that it's fixated initially on this object and then tracks it to here and then tracks it back. And when you do that, you get the same kind of effect, namely that the distance over which a far and a near object move is quite different. The near object moves over much, much greater distance than the far object, even though the eyes are tracking.
So this, then, being a basic physical fact, was then used in the course of evolution to create mechanisms that are sensitive to this differential motion. And, of course, because of the rate of motion also varies a little bit, it became possible to create mechanisms to make that computation to tell you where things are in depth. So here I'm going to show you an actual demo of this to make it clear to you.
In this case, again, we have a bunch of random dots, much like in the Bela Julesz random dot stereograms but just a single one. And everybody agrees there's no depth here. Is there any depth? Do you see any depth? So now what I'm going to do is I'm going to set this image into rocking motion. And when I do this, almost instantly, you're going to see something in depth. Are you ready?
So what you see here is are three levels, right, very clearly. In milliseconds, in 20 milliseconds, you can see this. And let me explain to you why you see this. If, OK, let me go back and do it again. If I keep this stable, you can see that the dots move over a great distance here, a lesser distance here, and practically not at all here. So there is a differential motion. And the greater the motion, the closer the image is in your analysis.
So that's called motion parallax. And then what you can do actually, you can play all kinds of games, do experiments in which you can present this kind of image. You can put this into each of the eyes separately. And you can present this image alone or you can present it paired with disparity for stereopsis. And you can do each separately or you can do the two together.
So let's now first summarize the essence of motion parallax. To derive depth information from motion parallax, neurons are needed that provide information about velocity and direction of motion and perhaps also about differential motion. Secondly, the majority of V1 cells are direction and velocity selective, as we had discussed before, and some appear also to be selective for differential motion, which I did not mention before. But, indeed, there are such cells in the visual cortex.
Now, the third important point is that such cells that are motion selective and direction selective and selective for differential motion are very, very common area MT. So those are some of the very, very basic facts. And now we can move on and ask what kind of brain activation occurs by stereopsis and motion parallax in normal and serial blind subjects using a recently developed technique, which is magnetic resonance imaging, functional, functional magnetic resonance imaging.
So how do you do this kind of stuff? Well, what you do here, here's an example, you have a very large stereoscope with a mirror at the end. And you have a subject who is lying down. And this whole unit, except not of course that part, is put into the magnet. And we have a magnet down here at MIT. Most of you probably have seen that. It's on the ground floor. So you can do this, and then you can present those images here.
And so the stereoscope will present two images and then you can vary this by rocking him back and forth either to present only motion parallax or present only stereopsis and to present both. And so now the question is, this is a very primitive question at this stage, where in the brain are these processes analyzed? And so you can find out what brain areas are active by doing this repeatedly collecting the fMRI data and then printing them out and looking at them to see what happens.
So I'm going to show you a couple examples of that. Here is the basic figure that the person sees but done in such a way that you can see it. Of course, he doesn't see anything like this. He just sees different depths. There are one, two, three, four, five, six, seven different depths here. And this rocks back and forth. And then you can, as I say, present this only with differential motion or you can present it only with disparity or you can present it with both.
And then finally, as a control, what you do is you can do the same thing. But you don't have any depth of any sort. You just have a flat surface rocking back and forth. And then when you do data analysis, you actually subtract the last one from the rest of the data so that you're not looking at the data for the activation just by the spots but for the activation that's specific for stereopsis or motion parallax.
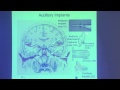
So now if you do this experiment, here's an example of a normal subject and a stereobind subject. And we have here a sagittal cut adding up the images sideways. And what you see here, this is posterior cortex, of course. Here in the normal subject, when you present only motion parallax, you only analyze motion parallax. But you have a huge amount of activation in the visual areas.
And then if you do the same thing when you do a binocular stereopsis only, you also get a great deal of activation, in quite similar set of areas. And then the big crucial test comes up. What happens if you present the stereo under monocular conditions when you don't see stereo? And if you do that, using this same calculation procedures, there is no brain activation here. And, therefore, what we see here is due, indeed, to the analysis that we do for stereopsis.
Now if you do the same experiment in a stereoblind subject who has been tested, on tests similar we had shown you, when that person even looks at it under binocular conditions, there is no brain activation meaning that this person doesn't have any mechanisms in the brain to analyze stereopsis. Now the fortunate thing is that we have these several different mechanisms for depth perception.
And so people who are stereoblind and have no analysis for disparity, they can still see depth reasonably well. And, indeed, they can get driver's license and all that, because we have all these other mechanisms that include, that we have talked about, motion parallax. So that then is one way of looking at it. Now the other way to look at it, especially when I ask as well, are the same brain areas doing both or what.
And so what you can do is instead of doing a sagittal section, you can take sections coronally like bang, bang, bang, bang like that and see what that looks like. And here's an example in which I've isolated the stereo. And here are a bunch of sections. And this shows the activation for stereopsis. You can see there are all kinds of areas that are being activated. And then if you do the same thing and just look at the parallax alone, here we have the activation for that.
And then lastly here, we do both of them. Now we can go back. The way to look at the question, how are these two areas, these two types of depth perception analyses, differently activating in the brain. And so I'm going to go back and forth between stereo and parallax. You can see, and that, you can see the difference. Now some regions, which have a perfect overlap, and there's some regions that are quite separate.
Notable here are these areas here, which are activated by stereo but not by parallax. So this then can provide you with an initial idea that there are some brain areas in which both of these are analyzed together. And there's some brain areas in which are uniquely analyzed for either stereopsis or motion parallax alone. Now this tells you where it takes place in the brain. But how it takes place requires a totally different approach.
Namely, the most comfortably to record from individual neurons in various areas just like I had shown you that nice work done by John [? Porgio ?] recording from the one demonstrating there that there are disparity selective neurons that are tuned that then provide the hardware, if you will, for being able to analyze stereoscopic depth. So that then summarizes what I wanted to tell you about motion parallax.
And now we are going to go on and talk about yet another important depth cue that is utilized by the brain, which is called shading. Now remember that our ability to use light to illuminate things is something that was practically nonexistent for endless millions of years. And so because of that, both animals and us, we have to heavily rely on information based on light coming from the sun, coming from above.
And shading is based on those millions of years of evolution utilizing the fact that most of the light that illuminates things comes from above. So there are all kinds of nice examples of this. And here is one of them. What you can do here is you can take a bunch of disks and set them up so. You can do this on a computer to make the upper part light and the lower part dark or the other way around, the upper part dark and lower part light.
And all of you readily can see that these images, the first and third row, seem to be protruding towards you. And the images in the second and fourth row seem to be receding. Now that is because the brain is interpreting that on the basis of the fact that the light at least used to come predominantly from above. So that is the basic arrangement for seeing depth.
And now I'm going to give you some demonstrations to indicate that this cue is actually quite powerful, even when you would not necessarily expect it to be. So these shading cues have also been extensively used in art work to provide an impression of depth. And I will show you some examples that will give you a sense of how that is done. So let me make one more point before I proceed that namely it is, indeed, the degree of illumination that's crucial here.
We have the same change from red to, sorry, from some greenish to yellowish. And you have no sense of depth here whatsoever. In other words, you do need the shading information, meaning the amount of light that's being reflected from various surfaces, that is crucial for perceiving depth. So now what we are going to do is we are going to present a series of slides that will highlight the power that shading has for the perception of depth.
So here is an example of how we do this. And the reason I'm showing this in some detail because if you really are interested in stuff like this, you can do all this on your own computer. You can play games, endless games with it. You can spend hours and hours having a lot of fun thinking about how depth works on the basis of shading. So what you have here are a whole bunch of disks. And each of these can be shaded differently by many different computer programs.
So that's what you can do. That's the basics. So now what we can do is we can play a game. And we can say, present just two different objects here. But we're going to present them repeatedly on a big display. And then we can shade these differently as we please. So here is a whole bunch of them. And all the rows, this, the first, third, and so on rows are the same shape and the second, fourth and so on are the other shape, these two shapes.
So we only have two shapes here that are juxtapositioned. Now what we can do is say, well, this is a peculiar sensation. I have a vague sense that there's something maybe in the third dimension. But it's not too well defined, because this is not in accordance with the rules and laws of shading of light coming from above. So now what we can do instead, we can selectively shade these to be in accordance with the rules of light coming from above to create shading and depth.
And when you do that, here's an example of that. What you can see here is a very compelling image of these protruding elements, sort of protruding to the left, right? Everybody see, have a strong sense of depth here? So now what you can do is you can play with it and decide, well, can we do something that, keeping the very, very same shapes, shade them differently and see what it does to our perception of depth.
And so what we are going to do next is we're going to take each of these elements here, the same ones here, and we're going to reverse the contrast. You see the contrast here on top is white and the bottom is black. So we're going to reverse that contrast. And when we do so, the question is what are you going to see. And if you do that, low and behold, you still have a strong sense of depth. But it's a very confusing sense. You may see sometimes these objects pointing to the left and sometimes to the right.
It's unstable, because you're confusing those computations that have evolved over millions of years for interpreting depth in terms of shading. Now you can play also some additional games. You can make this even more complicated, make more changes, and here is another one. You still have a feeling of depth. But it's totally confusing. It's very hard. You can't organize it any way, because it is not in accordance with the law of light coming from above to a real object.
And lastly, you can also make this so that it would be in accordance with the laws. But you can change it around so that you get a completely different perception, a strong sense of depth. It's still the very, very same elements that you had seen before. But now the shading is done, again, differently. And then now gives you, again, a unified sense of a display that is not conflicting. Because in this case, it's in accordance with that some of the basic principles of shading.
So now, what we can do next, having talked about stereo and we have talked about shading, is to look at some more of the demos. So let's go back to the stereoscope. And let's go back to the handouts. And so if you now come to the next page that has a heading called stereo and shading. So, again, take the stereoscope and we are going to look at these in steps.
So let's start by looking at the top display first, which is called stereo only. So if you look at that, first of all, if you just look at it without the stereoscope, you see pretty much a sort of flat display of a truncated pyramid. Then if you put the stereoscope there and look through it, you should see, if you look at it for a little while, that one of those sticks out towards you and the other one seems to recede. Does everybody see that?
So let's stop there for a minute, because I want to add one more fact here, which I should have mentioned earlier. So what you do here is-- so you have these two displays like that. And you have one image here and another image here. When you-- this is greatly exaggerated, these coming together like this. That means it's going to stick out towards you as you look at it. But if you do the opposite like that, they're further apart than the rest of them. Then actually you see it receding.
And that's why, if you now take away the stereoscope and look at it, you can see that the top left image is in each, or facing towards each other, whereas the other ones are facing away from each other. And that's what creates, that's what the brain interprets, as protruding versus receding using the stereoscope. So that is very similar, in a way, to what happens with shading.
So now if you look at the second image there, first without the stereoscope, what you see here, again, is one that sticks out just like in the original display. And the rest of them are receding. That's because the shading, the one that sticks out is light on top and dark on the bottom. And it's the obverse for the other ones. Now if you do the same thing looking through the stereoscope, what you will see is still some degree of depth, but it's not very pronounced. Because there is no corresponding disparity information.
But now if you look at the third display, where stereo and shading are in harmony, then what you see is an extremely compelling dramatic sense of depth with the top left one sticking out towards you and the other three receding. So shading appeared to have added to the compelling nature of the depth that you see through the stereoscope. Now the last image in here is that we put stereo and shading and conflict with each other. And when you do that, you can look at it, first with just one eye, then with the other eye. When you look at it with both of them, you, for a while, you see something unstable.
And when you see it well, eventually, you realize that there is a conflict there because of the shading and the stereo being in opposition to each other. Now then, this kind of effect, if you go to the next page, we're going to go now to page five, six, and seven. Again, what you need to do here is to look at it sideways with the F's on top. And when you look at this, those of you who can use your eyes so that they are divergent, and you look beyond it, then this is very much like, or it is the same actually, as an auto stereogram.
So if you look at this for a while, and you look beyond it, eventually it's going to gel. And when it gels, what you should see is where the F's are, the images are protruding towards you, and the others are receding. Now it may take you awhile. It's much more difficult than what we just did with the stereoscope. But you should be able to see that. How many of you are able to actually see those images? A little bit di-- move it back and forth a little bit slowly. And maybe eventually you manage it.
So as I say, where the F's are you see these images-- these truncated pyramids protruding towards you. And the rest of them are receding. If you have difficulty seeing this, I'm not surprised, because it takes a lot of practice. But once you get a sense of it, I think that you will enjoy doing this and actually showing it to some of your friends.
So then if you go to the next page, there we have added shading. And the shearing is the same everywhere. But the stereo cues are not. Once again, what happens is that they are stereo cues where the F's are stick out towards you much greater than the others.
They stick out a lot less because of the added stereo. And then, in the last demo there, the last page, we are putting, just like in that figure with a stereoscope, we are putting them into opposition with each other. And so when you look at these, this would be very difficult to see for a while. Because there's a tendency to see it differently for stereo and for motion parallax.
And so it's going to be an unstable percept. So what you can do then is you can play around with this at your leisure and especially once you become more proficient looking at all the stereograms, if you go and get one of these magic eye books to look at, you will be able to see these displays as well. So now, this is the one was the first one that I showed you. As I said, this one, with the F's, are the ones that should stick out closest to you. Once you see that, then you can go on to the next to add the shading or subtract the shading from it.
So now, an interesting question that arises is to what degree are we able, or are animals able, to integrate these different kinds of depth cues. And in particular, in this case, you're going to ask the question, what about integrating stereopsis, parallax, and shading. So the experiment is one done on monkeys in which you can present these cues either singly or in combination.
And we can ask the question, well, does the monkey do better with one or the other, or does he integrate really and does really much better when you provide all three cues. And so here is a procedure. What you do here, again, you have a rocking display like this, and you can present this either with shading as shown here or with motion parallax where it rocks back and forth, and lastly also with stereopsis.
So if you do that, the results you get are quite dramatic. What happens is shown here as a percent correct performance and here is the latency in milliseconds. And it shows that the monkey does extremely well when you present-- this is percent correct. This is degrees of disparity. The monkey does extremely well when you present all three cues and does worse when you present each of those cues alone.
Even more dramatic is the fact, and this is-- I keep coming back to this, that the ability for us to respond quickly to things is very important for survival. And here what we can see is that when you present all three cues, performance is much, much, much, much faster than when you present each of those alone. And, of course, as you might expect, when you present parallax only, because that's motion over time, that takes the longest to do.
So even though motion parallax cues are great, it became important in the course of evolution to create mechanisms that can detect these things more quickly and more efficiently. So now we come to yet another cue that we know very little about at the level of the brain or single units, because it's so complicated, which is called perspective. But I want you to just be aware of it and have a sense of it.
And here is one of those cartoon examples that gives you a very strong sense of depth. And you almost cringe. If you were there, you would worry that you would be falling down. This is done strictly by virtue of perspective. It's very similar to what you encounter all the time when you're driving down a road and the road seems to converge, even though you're not aware of it. But that's what's happening on the rental surface.
Because things further away are smaller than things that are close by. And that's when you look down a railroad track, the same thing happens, even though you know that the railroad track is not converging, it's going parallel. But because of the distances involved, that's what falls on the retina. And you're smart enough to know that even though that's what falls on the retina, you can make the right kind of interpretation.
Conversely, you can also compute the depth on the basis of that kind of convergence. Now here's another example of that, a much simpler way that people can do with experiments. Here we have a bunch of dots. And we have two basic cues that have to do with perspective. One of them is this gradually decreasing size of these dots. I should say elongated disks, if you will, and also that they are converging much like a railroad track converges.
And so we have a very strong sense of having a third dimension here. Now the fact that this is so strong can be mitigated by adding a few things here. If you add some more dots, it's not question as dramatic. And then if you start mixing up the sizes, you are beginning to lose it. And then if you totally mix it up, then you have no sense of that left at all. So it is that progression of steps and sizes and whatnot that gives you the sense of the depth of the images that you're looking at.
Now here's another converse example of this that is an illusory effect that what you see here is three barrels, if you will. And this barrel is a lot bigger than this barrel, right, or is it? Well, so what we're going to do here, we have an inducing element here by this hallway, if you will, with a door at the end. And we're going to remove this hallway keeping the barrels exactly as they are. And if you do that, low and behold, those barrels are all the same size.
It's induced by virtue of the surround that gives you a false sense of depth. So now let me show you another picture because of the purpose behind this. This a picture that's in a museum in Worcester, Massachusetts. And it was created by a fellow called Edward Savage. And it's a pretty unpleasant picture. But the main reason I'm showing this to you is that there seems to be very poor sense of depth in this picture.
Now the reason this is interesting is because when artists began, centuries ago in the 13th, 12th centuries, draw things, they did not have a concept of an understanding of how to create depth, a third dimension, in their drawings. So what they did eventually, they came up with a so-called vanishing point, and they drew very much like what we had here. Lines that converged at a point and then scaled the images accordingly rather than keeping it the same size.
And that way you got a good sense of depth. So now that has a number of interesting stories about it that we are going to discuss next time you talk about the perception of shapes, OK, patterns. But I will leave that discussion until that. What I'm going to do next, however, I'm going to try to give you a sense of how important stereopsis can be for the perception of fine depths.
And so to do that, what I'm going--I'm going to show you actually a film. And here what we have is a so-called needle test. What you have here is a fine needle protruding. And here we have a bunch of different size circular openings, a little bit like a needle, but it's round. And the task is to take these one at a time and hang them up. And one can time how quickly you can do that, or you can make a film to see how well you can do it.
And then what we can do is we can test the subject under binocular conditions, and test them under monocular conditions. So I'm going to show you a film of this, actually two films. It will just take just few seconds to do it. OK, be ready, it's going to come up in a second. OK, here's the subject under binocular viewing conditions. So that's the condition under binocular viewing.
And now I'm going to show it to you, same subject, same time, but with one eye closed off. So that then just even looking at it without taking any careful measurements. It's obvious that it's much, much more difficult to thread a needle under monocular than under binocular viewing conditions.
And so what you can do is when you go home, and next time you want to sew something up, try threading the needle with one eye closed and with the two eyes open. And you will see immediately what a huge difference it is. And that difference, therefore, is due to you're having the mechanism of steropsis. Just a few seconds here.
Another test that has been used in a similar fashion which allows you to actually calculate exactly what your error is in reaching, you can have a subject sit in front of one of these touch panels, and then do this experiment either binocularly or monocularly. And after he presses this a dot comes up, and then the person has to touch it. And you have about 30 or 40 trials like that. And then you have recorded where the person touched. And, therefore, you can calculate the error between where we touched and where the dot is.
And then, again, you get a huge effect between monocular and binocular viewing conditions. Now when you come to monocular and binocular viewing conditions, another thing important to test is to what degree a person who does or does not have stereopsis is capable of integrating information between the two eyes. So to do that, we have here examples of what is called binocular integration.
So what we do here, again, you can use a stereoscope. You look at a monitor. And this represent the left eye, this is the right eye. And you flash these on. If you integrate this, this is what you see. This would be actually what you would show in the control part of the experiment. So you see the Star of David. And if a subject is shown this, and they don't see the Star of David, you worry that their ability to integrate the information between the two eyes is deficient.
And I would say 90% of the cases, those people who are deficient on this also show major deficiency in stereoscopic viewing. Now another way to do this is an experiment in which you can present two words here, sud and try, so the two are separate. And when you present them simultaneously, you actually see the word sturdy. So you ask the subject, please tell us what do you see. What is it word you see.
And the subject says sud. And the subject says try, then you know that that subject sees, if he says try, he sees mostly with his right and prefers it, doesn't see too well with his left eye. If he says sturdy, then he integrates the two. And, therefore, you can safely say that this guy has very good integration between the two eyes. So what I would like to do next then is to provide you with any questions that you have. This was a complicated topic, that you have, and then we are going to summarize.
Does anybody have a question about motion parallax, stereopsis, and so on? Let me maybe add one more important factor. Your eyes are separated only by so many centimeters. Now, can you think of an animal where there's a much larger separation?
AUDIENCE: Hammerheads.
PROFESSOR: The hammerhead shark. Yeah, that has a separation of over a foot between the two eyes. And so you could ask the question, why on earth did that animal evolve to such a huge separation between the two eyes? Well, that brings one to yet another interesting point. This I think may have started during the Second World War. It was realized that when you're flying over some territory, where there are all kinds of weapons and whatnot, which are well camouflaged, that just looking down at them, you can't see them.
But obviously if you're going to have a tank or you're going to have a gun or other that may be more like a cannon, it sticks out of the ground. So it was discovered that if you had in your airplane two lenses which are far apart, that would greatly magnify the depth. You could defeat that camouflage. And you could find those weapons down there by virtue of the fact they're sticking out of the ground.
So the fact then is that the more you separate the images from the two eyes, if you will, or your two cameras, the more likely it is that you can calculate the disparity of information between the two images. So that then is probably one of the reasons, not the sole reason, but maybe one of the reasons why, in some animals, is an excessive separation between the two eyes.
And that brings me to get me to yet another point, which is that stereopsis actually works best at relatively short distances, like threading a needle. It doesn't work too well beyond, I don't know, 10 feet or so. It becomes progressively less effective. But at short distance, it's very effective. And so I presume also many animals that have to hunt for food are able to utilize the mechanism of stereopsis, because everything is at a close distance when they hunt for food on the ground.
And by contrast, when you talk about motion parallax, that works extremely well over very long distances. So does anybody have any questions about motion parallax or about steropsis? Oh, once again, I'm crystal clear, huh? So, therefore, I think it's time for us to summarize what we had covered today. First of all, there are numerous mechanisms that have emerged for analyzing depth.
And they include the ocular motor cues, which are vergence an accommodation and then the binocular cue of stereopsis and then the monocular cues of parallax shading and perspective. Then you have several cortical structures that process stereopsis. You don't have one specific brain area that uniquely does this. The number of disparities that are represented in the brain, as studies in the area of the one by John [? Porgio, ?] is limited.
And maybe, maybe four, but there may be six, but certainly there are not a large number of them. And so it's analogous to the way things had been resolved for us to be able to process color. Utilizing motion parallax for depth processing necessitates neuron specific for direction, velocity, and differential velocity. Several areas getting V1 and MT process motion parallax, which I did not say.
But indeed, if you make a lesion in area MT, you go get a deficit in motion parallax, even thought you don't get a major deficit in steropsis. Now, area MT combines the analysis of motion parallax, depth, and flicker. However, these analyses are also carried out by several other structures as I've already said. And lastly, little is know at present about the manner in which information about shading and prospective are analyzed in the brain. And hopefully, that will be one of the future tasks by neuroscientists.
And so if any of you ever get involved in neuroscience, this certainly is a big open area that we hope people will start to analyze. So that then is the essence of what I wanted to cover today. And once again, if any of you has a question, please, please don't hesitate to ask. I'll be very happy to answer them. OK, lastly then, did everybody sign the attendance sheet? If not, please come up after the class and sign your name to it.
Very good. So next time then, we are going to talk about pattern perception. And hopefully you will find that also interesting.