Lec 20: Sound localization 1: Psychophysics and neural circuits

• Download English-US transcript (PDF)

The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high-quality educational resources for free. To make a donation, or to view additional materials from hundreds of MIT courses, visit MIT OpenCourseWare at ocw.mit.edu.

PROFESSOR: Last time we were talking about descending auditory pathways and the brainstem reflexes, which are, in some sense, part of those descending pathways. And especially how they protect our sense of hearing from damage. So I had a question about subway noise on the Red Line in Boston. And I was asking around at my hospital and nobody seems to have measured it. But I saw online that there were some measurements of subway noise in New York City. And that it can actually be damaging if you get exposed to it for long enough. So there's a little news clipping about subway noise.

So I don't ride the Red Line very often. I ride a commuter train from Lincoln, where I live, to North Station. And when that train comes in and puts on its brakes, it's incredibly shrill. And I always plug my years. And about half the people do and the other half have hearing loss, I guess, or whatever. It's not really a laughing matter.

So any questions from last time? Of course, the brainstem reflexes we were talking about are also good for other functions, like reducing the effects of noise masking, allowing selective attention, those types of functions. I also have experimental evidence in support of them. So if there aren't questions from last time, we are going to shift gears a little bit and talk about something completely different, which is sound localization.

And so today's roadmap is titled-- headlined-- "Sounds Localization." And we're going to be talking about the kind of localization using binaural cues, where you have two ears. And because you have two ears and because sound sources are located off your midline for the most part, we have some very prominent cues called Interaural Time Differences, ITDs, and Interaural Level Differences, ILDs.

OK, so we'll talk about what those are, how big they are. We'll talk about performance for localizing sounds in humans. How good are we at doing that task?

We'll have some demonstrations. One of them I'm going to give you in the room here and the other three demos we'll have to listen to in headphones because we want to use just one of these cues, interaural time or interaural level differences. And for the most part in a room, in an ordinary environment, they're mixed up together. They come together. But using headphones we can isolate and play just one or the other.

Then, we'll launch into the neural processing of one of these cues, ITDs, in a part of the superior olivary complex called the Medial Superior Olive, or the MSO. And so just a heads up here, last lecture we were talking about the neurons in the olive called the medial olivocochlear neurons. Those are completely different. They have nothing to do with sound localization. So those were the MOC neurons. And today, we're talking about MSO neurons. These are completely different. They're neurons in a major part of the superior olive called the medial superior olive because it's in the medial part.

And then finally, we'll end up with a discussion of the assignment. We have a written assignment for audition that's due in a few weeks. But it is based, in large part, on today's lecture. So it talks about the model of neural processing in the MSO.

And another heads up. I've added a tiny little bit to the end of the assignment. And we'll talk about what I've added. And that revised assignment is now posted on the course website.

We'll talk about that at the end of today's class. So sound localization using binaural cues. What are the two cues?

Well, they're the interaural time differences and interaural level differences. And this subject, cat, is listening to this sound source at the black dot. The sound source is emitting sound. And because sound doesn't travel instantaneously through air, the sound located off to the right of the subject strikes the subject's right ear first, and then there's a little bit of time before it gets around to the left ear, which is pointed away from the source.

OK, so if this sound source is emitting a click as diagrammed here, so this y-axis could be the sound pressure level at the subject's right and left eardrums as a function of time. This is the time axis. So obviously, the sound source is off to the right. The right ear is going to receive the sound pressure first. And then a little bit later, the left ear will receive the sound source. I mean, will receive the click sound.

If the sound emitted is, instead of a click, a continuous wave, like a sinusoidal wave. It'll be delayed the same amount right versus left. So here's the right ear sound pressure level, and then here is the delayed version that appears at the left eardrum. Just a delayed version. So how much is the delay?

Well, it depends on things like the velocity of sound in air. Sound in air. I think we had this in the very first lecture. 340 meters per second in air.

Now, it depends a little bit on the temperature of the air. And it depends a little bit on the barometric pressure, but these factors change at less than 1%. So about 340 meters per second in air. So knowing how many meters between the right and left ear, you can calculate for various positions of the sound source the interaural time difference.

Now, if you have a big head, so that the left and right ears are separated very far apart, obviously you're going to get a bigger interaural time difference than if you have a tiny, little head. Like a mouse sort or a bat. The smallest animals have very close eardrums, so they have very small interaural time differences.

OK, now a couple other things I should say about both of these cues, interaural time differences and interaural level differences, is they help us detect where the sound is coming from in the azimuthal plane, which is the horizontal plane. So here's a schematic of a person's head with the left ear. This is the front of the head. And the right ear is behind, so you can't see it.

And so azimuth is in the horizontal plane. And that's where interaural time difference changes as a function of position.

The other plane perpendicular to that is the plane of elevation. So for me going straight up and straight down is the elevation of the sound source. And you can imagine if there's a sound source straight ahead, it's going to strike my two eardrums at the same time because the path length from the source to the eardrums is the same.

And if that sound source moves up from being straight ahead to, say, elevated from straight ahead. But still, it's in the same place relative to the eardrums. The path from the sound source to the two eardrums is going to be the same. So the ITD does not change as a function of sound source elevation. So these binaural cues that we're talking about here do not change as a function of elevation. So how do we detect the change in elevation of a sound source?

Well, we talked earlier in the course. I think in the very first lecture about the so-called "pinna" cues. And so we have these external ears, the pinnae. And they help us greatly in detecting sounds that differ in elevation because they put onto the sound spectrum some very prominent peaks and nulls. And those peaks and nulls change as a function of sound elevation.

So go back to the very first lecture that I gave you and review that. And we read a paper where if you distort the pinnae by putting little plastic or clay ear molds in your pinnae, your detectability of sound sources that change in elevation goes to pot. You can't do it anymore.

But if you go out and re-experience sound with those little distortions of your pinnae and come back in a few weeks, you can re-learn how to detect changes in sound source elevation. And in those kinds of things, two comments.

Number one, you don't need two ears. You can detect change in sound source elevation with just one ear, because one ear has a pinna and it works just fine in changing the spectrum from one ear. And number two, your sensitivity to small changes in sound source elevation is not very good. So if you change the sound source elevation of 10 degrees, most people cannot detect that change. The minimum changes in sound elevation that are detectable are more like 30 degrees, which is a pretty big change.

We'll see using the binaural cues to detect changes in sound source azimuth, we're down to about one degree using these binaural cues. So they're much better. You're much more accurate in terms of localizing sound in azimuth than you are in elevation.

Secondly, I should have mentioned here when we had this time delay for the ongoing signal, like a sinusoid wave, that is equivalent to a phase difference. The phase is what engineers use to define where and when a sinusoidal source starts and ends. So engineers talk about a sinusoid going through a 360 degree phase for one cycle.

And so this sinusoid is delayed about a quarter cycle relative to the right ear one. And so it has a phase lag or a phase difference of about 90 degrees. So you can talk about interaural phase differences for continuous waveforms, like sinusoids. And you talk about them in terms of the number of degrees of phase difference.

And of course, to convert from one to the other you need to know the frequency that you're talking about. Because if you're dealing with a high-frequency sinusoid that goes back and forth a lot of times, you have to know that to calculate the interaural time difference.

But some of our demos that we listened to will quote the interaural delay in terms of phase. An interaural phase difference.

Now, the second cue is interaural level difference. And here's the same subject. Here's the same sound source. The sound is coming to the subject's right ear and it's a high level there because there's a direct pathway. But the sound to get to the left ear of the subject has to go around the subject's head. And sound does bend around a wall. So I can go out in the hall and I can say, class, can you still hear me?

Yes, you can still hear me, right? The sound is bending around. Of course, some of it's reflecting. Sound bends around, but some sound bends around more easily and more effectively than others. And obviously, this sound bent around. There's still sound at the subject's left ear. This should actually be delayed because it took longer. But the purpose here is that it's lower in amplitude and it's not vanishingly small. So there's less sound over the subject's left ear. And this is the interaural level difference.

This interaural level difference, as we'll see in just a minute, depends greatly on sound frequency. Such that very low-frequency sounds, because they have a long wavelength relative to the object they're bending around. Because of their physical characteristics, they bend around very well. And so the interaural level difference, as we'll see, is almost 0 for low frequencies.

For very high frequencies, there's a big, so-called sound shadow. They don't bend around an object the size of the had very easily. And so there's a big interaural level difference for high frequencies. So we think of these cues then as being very important for high frequencies. So let me just note that down here.

So ILDs-- I'll use a different color. Important. And let me show you some data to support that then.

These are some data taken for the two cues for a human head. And how do we get these data?

Well, we can take two small microphones and put them down in our ear canals very close to our eardrums. And we can measure the time difference and the level difference.

And so if you were to do this, you'd seat a subject in an anechoic room. An anechoic room is one that doesn't have any echoes coming off the walls and the ceilings. So that the subject just experiences the direct sound from whatever sound source. And the sound source we're going to move around. So this x-axis is the sound source position in angles from directly ahead. So directly ahead is 0. And higher angles is off, let's say, to one side. And directly off to the side is 90 degrees. And then behind the subject is greater than 90 degrees. And directly behind the subject will be 180 degrees. So this is degrees of azimuth from directly ahead.

This top graph shows you the interaural time differences and the bottom graph shows you the interaural level differences. So how do we compute time from the microphone signals?

Well, we simply take our microphones and run them to an oscilloscope. So here's the head. Here's microphone 1 in the ear canal on the left side. Here's microphone 2 in the ear canal on the right side. You send the wires from those two signals to an oscilloscope. The top channel will be the signal coming from the left side. The lower channel is the signal coming from the right side. And this device, the oscilloscope, plots the voltage, which is equivalent to the pressure as a function of time.

And we can measure the time when this sound starts and the delay, or interaural time difference, when the second ear starts. So it's very simple to measure.

Now that said, it's also very simple to assume that the human head is just a sphere. And it's simple to compute knowing the distance between the two ears and the angle of the sound source. It's very simple to assume that this human head is a sphere. And I think this solid line is assuming it's a sphere. And the dashed line with x's are the experimental data. The data are pretty close to the assumption that the human head is a sphere for interaural time differences.

And here's the ITD plotted as a function of the angle. As you would expect if the sound source is straight ahead-- that is 0 degrees angle-- the ITD is 0. The sound takes the same time to get to the two ears because it's straight ahead.

Now as you move the sound over to one side, it's going to get to one ear first and the other ear a little bit later. And so the ITD becomes bigger than 0. And it goes up. And the maximal ITD, as you would expect when the sound is directly off to the side, which is at 90 degrees. And what are the units here?

You probably can't read them, but they go from 0 to 0.6. And those units are milliseconds. So the ITDs go from 0 to 0.6 milliseconds for the human head. So millisecond is a thousandth of a second. It's pretty small. It's less than 1 millisecond for the maximum ITD.

And so you can quote this in terms of microseconds as well. So this would be a total, a maximal ITD of 600 microseconds. OK. Now, how about interaural level differences?

They are in the lower panel. And these are all measured values. They're not computed. I don't know why, you could compute them easily. Maybe it's because of the pinna. The pinna introduces another piece of complexity that's a little bit different from the head being an absolute sphere. So these are measured. And these are, again, plotted as a function of the azimuth. 0 degrees is straight ahead, 90 degrees is off to one side, and 180 degrees of azimuth is behind the subject.

And these, I said the ILDs depend on frequency. So these are separate plots for a bunch of different frequencies. Down at the bottom is a very low frequency, 200 Hertz. This is our standard center of the human hearing range, 1,000 Hertz. And this is a very high frequency at the top, 6,000 Hertz.

And as you can see quite clearly, a 200 Hertz, like I said before, this frequency of sound bends around very nicely for objects the size of the human head. And so even if you have the sound source all the way to the right, The ILD for 200 Hertz is 0. You don't have an ILD, essentially, for such low frequencies.

For our mid-human hearing frequency, the ILD starts out at 0, straight ahead, and climbs to perhaps 6 or 8 dB. As the sound source moves off to the side, it's not behaving like a perfect sphere. So a perfect sphere, the ILD would go up and be maximal at 90 degrees. So maybe this is the effect of the pinna. This is not doing that, but it's certainly climbing.

The biggest ILD is found at these highest frequencies. So for 6,000 Hertz, the ILD climbs from 0 up to an ILD of 20 dB as the sound is located off to one side. And that's a huge cue for localization of sounds.

So maybe you can remember back to the very first of my lectures, where we had the decibel demonstration. We changed decibel levels. I think this was a noise that we presented in changing steps of 6 dB. And it was clearly obvious when you change-- this is now binaural level at 6 dB. 3 dB changes in noise level were obvious. A 1 dB change in noise level as we stepped through was obvious after you'd gone through a few steps. But maybe from one to the next step was not obvious.

Clearly, a 20 dB difference between the two ears is a huge cue. How can we confirm that that's a huge cue?

Well, we can take a these cues and present them through headphones. And it's very easy to set up a circuit so that you have a signal coming into the two headphones. And in one channel, you put a device called an attenuator that attenuates the signal. So why not use an amplifier that amplifies the signal?

Well, amplifiers are active devices. And if you amplify sounds, inevitably you add a little bit of distortion. So it's easier to just attenuate the sound. Attenuators are passive devices and you can cut the sound to one channel 20 dB and it sounds like a huge effect. And you say, oh, wow. That sound disappeared in one ear. It sounds like it's coming from the other.

You can cut the sound by 6 dB, a huge effect. Cut it by 3 dB, a big effect. And you cut it by 1 dB and the person says, well, before when the sound was the same in the two ears, the sound was straight ahead. When you changed it 1 dB, it sounded like it just moved a little bit from straight ahead. So it turns out that 1 dB is not only our just detectable level in sounds when we present them to the two ears, but when we vary the interaural level difference.

So 1 dB is our just noticeable difference for ILD. OK, we can play that trick with headphones. Do good tests on that.

So clearly, these cues are very important at high frequencies because they're the salient cues. What about at low frequency?

Since we don't have an interaural level difference, you would assume that we're going to use interaural time differences at low frequencies. And you'd be correct. Much of the evidence suggests that ITDs are used at low frequencies and ILDs, because they're big at high frequencies-- those are the cues used there. And why don't we use ITDs at high frequencies?

OK, there is nothing in the physical characteristics of sound. For example, the sound velocity doesn't depend on frequency. It's constant no matter what the frequency of the sound. So you're going to get the same ITD for low frequencies and for high frequencies.

Well, if you think about it a little bit, there is a reason where high-frequency ITDs are less useful. At some frequencies, this sound waveform is going to go back and forth so quickly that it might hit the right ear. And then by the time it leaks around to the left ear, it goes through a complete cycle. Then, what are we left with?

We're left with right and left looking exactly the same. There's a big time difference, an interaural phase difference of 360 degrees. But we'll never be able to perceive that because the sound is, again, the same at the two ears.

And it turns out, of course, that depends on how widely spaced your ears are. For the size of a human head, the phase goes completely through one cycle at a frequency of 1.6 kilohertz. And that's pretty centered in your hearing range. 1 kilohertz is about the middle of your hearing range. 1.6 is pretty close. So above 1.6 kilohertz, ITDs become ambiguous.

And so we think of that as the time where ITDs fall out and ILDs become important. So ITDs are ambiguous for humans above 1 kilohertz.

Now, that argument, of course, is for ongoing interaural time differences. If you start the sound, no matter what frequency, you're going to have an onset difference. You can start a 2 kilohertz sound. The left ear will get it first, and then the right ear a little bit later, depending on where it's located and the degree of separation of your two ears. But that's just one cue.

And if these things are repeated back and forth thousands of times, depending on how long they're on for, for low-frequency sounds you'll get those thousands of cues. But for high frequencies, you'll just get the onset.

So for high frequencies, we think of these frequencies as not being useful for ITDs for these ongoing cues, like interaural phase differences. OK, is that clear? Any questions? All right.

Let's see how good we are in terms of performance. Sound localization is accurate and humans have excellent performance. How do we measure such performance?

Well, we take an observer. We sit them down in a room or in free field where there's only the direct sound coming from the sound source. And no reflections off the walls or echoes off the ceiling or floor. And we say to this observer, OK, here's the sound directly ahead. And then we move the sound source. And this can be a physical speaker. We move the speaker over a little bit and so we change azimuth. And we ask the person, was that azimuth detectable? We say, is that the same or different from straight ahead?

So if straight ahead is here and we move the speaker over to here and we say to the person, same or different? Same position or different position?

And the person says, yeah, sure. That's different. And then we instead say, OK, straight ahead is here and we're going to move it less. The person says, sure, I can detect that. No problem. It moved off to the right. And this is, again, without any visual cues. So the speaker has to be behind a screen. So it's only auditory cues that allow you detect this change in movement.

So we do it a third time, straight ahead, and we move it such a small degree that the person says, I don't hear that change at all. And we titrate the level of movement until we get what's called the minimum audible angle in degrees. And we can do that for a whole bunch of different frequencies.

And when we do that with sound sources, such that the initial position is 0 degrees straight ahead, we get this curve linked by the black dots. Such that at low frequencies, the minimum audible angles approach, in the best performance, 1 degree of azimuth. An observer can tell the difference between 0 degrees straight ahead and 1 degree to the right or 1 degree to the left. It's very impressive performance.

In the middle frequencies, where the ITDs are starting to break down and become ambiguous, our performance is not so good. Minimum audible angles go up to perhaps 3 degrees. And then they get a little bit better at the very high frequencies. And remember here, we said that the interaural level differences were very salient.

So at 5 kilohertz, there was a 20 dB difference. And we come back down, maybe not to 1 degree minimum audible angle, but maybe to 2. So almost as good. And then at very high frequencies, we get worse again.

Now, we can take these same subjects and we can go back to the physical cues. Let's say at a 1 degree minimum audible angle at low frequencies where ITDs are important cues, what is the interaural time difference that a subject can just barely detect?

Well, if you had a magnifying glass, you could read it off this curve. Because 1 degree is a very small angle on this scale. But you can calculate it from the sphere, right?

And it turns out that the prediction is that for the minimum audible angle of 1 degree, the interaural time difference is 10. Now, this is microseconds. It's calculated to be 10 microseconds. Where we perform the best, where we're using ITDs, this minimum audible angle, change in sound source of 1 degree corresponds to a change of ITD of 10 microseconds. That seems like an unbelievably small instant in time.

But once again, if you take the subject and now instead of an attenuator in one channel, you have a circuit that delays one ear relative to the other. And you say to the subject, OK, with no delay, what did it sound like?

Straight ahead. OK? Then you put your delay in and you say, what does it sound like now?

And the subject says, it just barely sounds like it moved a little bit off to one side. And in fact, 10 microseconds is the just noticeable difference for ITD in headphones, which is evidence then that we are using these ITDs at the low frequencies for sound localization.

Now, you can, as we said, play the same trick here. Minimum audible angle at 2 degrees. Go to the ILD curves. And I'll try to get your magnifying glass out here at 5 kilohertz. Look at where 2 degrees is.

And it turns out that the interaural level difference there is 1 dB. Play it in headphones. The subject says, yeah, it sounds like it's just a little bit off center. So it all fits with these presentations in free fields and these interaural level cues measured in free fields with what you get in headphones.

Now, we have some demos of these things. And I have several kinds of demos. So let's do the real fun one first. The problem with fun demos is sometimes they don't work.

So this has worked in some classes and has not worked in other classes. I have a sound source. It has a lot of high frequencies. You can probably appreciate that, jangling keys. And I would like to be able to just say, OK, I'm going to just give you interaural level differences. Probably, that's what you'll get here with high frequency sounds.

But I can't assume that it's also not going to have some ITDs because in this room there's going to be differences in time from the sound source to your two ears. So I'm really going to give you both cues, but let's start with this demo before we go on to headphones.

I'm going to jangle these keys. And I'm going to ask you, because you are such visual people, to cover your eyes while I jangle the keys. Don't cover yet, because what I want you to do is to tell me where the keys are coming from with your other hand. I want you to point where you think the keys are coming from.

And at the end, after you hear the sound, keep pointing, and look and see how good you were. OK? So everybody, cover your eyes.

[KEYS JANGLING]

OK? Now, uncover your eyes and keep pointing. OK, so we're doing pretty well here. Maybe 20 degree angle, but most of you guys are on. All of you guys are on. All right, let's do it once more. So blindfold yourself. Going to move the position of the keys.

[KEYS JANGLING]

OK, open your eyes and keep pointing. OK, you guys are good. Maybe like 20 degrees. I changed the elevation a little bit too, so you guys are making mistakes in elevation. You guys are good. OK.

Now, since I claimed to you that we're using two ears, I would like you to plug one ear, blindfold yourself. Now, it's going to be a little bit of a trick to point, right?

So I don't know how you're going to point. You can point with your elbow or you can do whatever you want to point.

AUDIENCE: Close your eyes.

PROFESSOR: You can close your eyes. OK, if you're truthful. You can close your eyes, OK.

[KEYS JANGLING]

OK, open up and we'll see how you did. You guys are good. There's an error. That's the biggest error I've seen so far. This is an error, like at least 45 degrees. This is an era here. So we're doing more poorly. Let's plug the other ear and I'll repeat the sound. OK, close your eyes.

[KEYS JANGLING]

OK, open your eyes and keep pointing. These are some errors. Oh, this is a big error. This is an error. OK, so we're clearly, anecdotally, getting worse. OK.

Now, the ultimate test, plug one ear. And in your remaining ear, distort your pinna because I claimed that your pinna cues were helping you. And I really don't know how you're going to point here.

[KEYS JANGLING]

OK. Now, open. Just continue to point if you can. OK, so that's a 90 degree error. You guys are pretty good. You have an error here. You guys are good. This is an error. And where were you pointing? You were pointing correctly, yeah. So good. OK. Let me try it one more time with distorting pinna and plugging one ear.

[KEYS JANGLING]

OK, show me where you were pointing. You guys are good.

AUDIENCE: Nice.

PROFESSOR: This is a little-- was it harder--

AUDIENCE: It's impossible.

PROFESSOR: It's impossible. So you were guessing? That's why it doesn't work.

AUDIENCE: It all sounds the same. It all literally sounds the same.

PROFESSOR: What's that?

AUDIENCE: It all sounds the same.

PROFESSOR: It all sounds the same with the pinna distorted. Right. OK, this is a huge error.

AUDIENCE: Yeah.

PROFESSOR: OK. I think it worked. Pinna is very important in distinguishing front versus back. Interaural time and level differences are equivalent for front and back. So how do we know what's front and back?

Well, the pinna cues are very important for that. Otherwise, you have subjects reporting confusion between front and back. A lot of the times to eliminate front-back confusions, experimenters will require subjects to point in the frontal [? hemisphere. ?] And say, it's not in the back. I give you that it's in the front.

OK, so we have more control demonstrations that can be presented during headphones. And we have demonstration of these two cues. And there are three demonstrations. So the first two demonstrations are ITDs. And the first one uses tones. So a tone is a sine wave. And it's going to give you tones of 500 Hertz and 2,000 Hertz. So the low frequency and higher frequency are heard with alternating interaural phases of plus and minus 45 degrees.

So let me just remind you, we saw here an interaural phase difference of about 90 degrees. So this is going to be half of that. Interaural phase differences of 45 degrees for these 2 pure tones.

The second one for ITDs is going to use clicks. And they're going to be repeated just like my hand clapping.

Next, the interaural arrival time of a click is varied. And it doesn't tell you how big the ITD is. The apparent location of the click appears to move. And to me, it sounds like the clicks are going around. Somebody clapping their hands moving around in a circle.

Now, when you listen to these demos with earphones or ear buds, sometimes you get the impression that wherever it's coming from, it's sort of like on the surface of your head. It's not way out there. That may be because you have lost some of the room acoustics. Certainly, you're not listening to reflections. But you've also lost the effects of the pinna, which filter things in such a way that they sound more roomy or out there. These things sort of sound internal, but they still appear to change in azimuth. And I think this click demonstration is the most vivid of the three.

The final demonstration is interaural level differences. The overall interaural level difference of a 100 and 4,000 tone is varied. Now, heads up here. This low-frequency tone is never going to have an ILD in normal free-field acoustics. It's just never going to happen because of the size of your head. You have to have a huge head to cause a sound shadow for that low of a frequency.

But you can certainly just-- as easily as for high frequencies, present that in headphones. And it is perceptually obvious, OK?

So there's these three demos. So how many people have them on your machines and have earphones?

OK, so you guys can just go right ahead. How does it appear? Are they in order? Do they have names?

AUDIENCE: You can just download them from Stellar.

PROFESSOR: Yeah. You can download them from Stellar if you haven't already. They should be on the course website. So just do them in sequence.

People who don't have them on their laptops can listen up here. I have these listening stations. So whoever wants to come up and listen can come up.

Could you hear them going around your head? That's, to me, the most vivid. Comments about the others?

This last one is kind of piercing for the high frequency, right? And it still sounds like it's moving around. What about for this lower frequency? Did it sound like it was moving around?

OK, even though that stimulus is not present in free-field sound. You will never hear that without headphones. It's perceptually obviously. Now, how about this ITD?

To me, this 500 Hertz interaural phase difference is obvious, but the 2,000 Hertz wasn't.

AUDIENCE: [INAUDIBLE].

PROFESSOR: Clear for you. Any speculation on why that would be true?

AUDIENCE: [INAUDIBLE].

PROFESSOR: OK, what we're saying is then that this is the left ear for the low frequency and the right ear is, what? 45 degrees? So it's going to be sort of like this. OK, that's for maybe the lower frequency. And the higher frequency is quite a bit higher, right?

It's more than twice the frequency. So it's more than twice as much. I'm a terrible artist, but it's going to go back and forth faster. And this is going to be delayed 45 degrees. So because this is going faster, it's a smaller time difference for the high frequency. So you might say, OK, it's just a smaller time difference. And that's why it's harder for us to distinguish it.

But remember the concept that we had of phase locking of the auditory nerve. In the auditory nerve, the left auditory nerve is going to fire some spikes at some point in the stimulus waveform. The right auditory nerve is going to fire some spikes at a corresponding point in the stimulus waveform for the first cycle. OK, let's repeat it for the second cycle.

Going to fire in there somewhere. This one's going to fire in there somewhere. And remember, cycles are going by pretty quickly. There's lots of time. So you can build up a response pattern where you have thousands of spikes there, thousands of spikes here. And these two auditory nerves are coming into the brain. They're synapsing in the left and right cochlear nucleus. Cochlear nuclei. The cochlear nuclei are then projecting centrally. And at some places, the left and the right-side pathways converge.

There's a comparator then that's comparing the arrival time and it's saying the left ear signal is getting to me first and the right ear is a little bit delayed. What happens with the higher frequency?

So this is an interesting high frequency. This is the 2,000 Hertz. What happens to the phase locking for frequencies above 1,000 Hertz? It declines, right?

So instead of a nice synchronized pattern, this left auditory nerve is going to respond. The right is going to respond. But from successive cycle to cycle, the pattern is not going to be synced to a particular point in the stimulus waveform. So instead of getting a nice synchronized pattern, it's going to be unsynchronized.

And maybe for some stimulus presentations, the right-side spike is going to come in earlier than the left side. And the comparator is going to say, WTF. I don't know where the sound is coming from, right?

So the fact that phase locking breaks down means that the timing at wherever the central comparator is, it's not synchronized. Timing here is synchronized. The timing here is not synchronized.

And we're claiming with this psychophysical metrics that we can detect a difference between the left and the right ear minimally at 10 microseconds. With synchronized patterns at least.

Now, let me just draw-- it's not too surprised. Everybody understands why when you break down phase locking, you don't have a temporal code anymore?

Let me show you the spike waveforms for one spike coming in in the left side and one spike coming in the right side that are delayed by this minimal time of 10 microseconds.

So here is spike, let's say the left side. So to draw a spike coming in from the right side delayed 10 microseconds, I need to know the time base here. How long does it take a spike to fire in the central nervous system? What is the duration here? What's the time scale here?

AUDIENCE: 1 millisecond.

PROFESSOR: 1 millisecond, very good. OK, so now I'm going to draw a right-side spike coming in that's delayed by 10 microseconds. And it's pretty easy to do. I'm going to do it in a different color, but it overlays here very clearly. I didn't draw anything because on this time [? base, ?] they're almost perceptually indistinguishable.

OK, so the right side here delayed 10 microseconds. That's the wonderful property of this system that we have relatively large, long inputs coming into the CNS. And we can, at the limits of our perception, distinguish delays of a very short time scale on the order of 10 microseconds. That's the impressive nature of this central comparator, wherever it is. And we're about to talk about where it is now. So let's look at where it is in the brain.

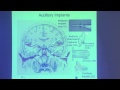
We had our block diagram of the central auditory pathway before. And here's kind of a simplified diagram. This is the left side and the right side of the brainstem with the two auditory nerves coming into the two cochlear nuclei. And in the cochlear nuclei, we discussed that the auditory nerve synapses and cochlear nucleus neurons then pick up the message.

Now, in one sense the cochlear nucleus neurons know only about what's going on on that side of the brain, or that auditory nerve. They're not getting inputs from the other side. So they're not binaural, if you will.

The first places where you have binaural input in the auditory pathway are centers like the superior olivary complex. And we talked about that before, Superior Olivary Complex, or SOC, having a bunch of not only binaural inputs but a bunch of different sub-nuclei. That's why it's called a complex.

One of the most important of those sub-nuclei is the Medial Superior Olive indicated here by MSO. And the MSO gets input from the left cochlear nucleus if it's the left MSO. And it also gets input from the right cochlear nucleus.

And here is a very good guess, at least, for where the central comparator is on the basis of interaural time differences. And this was appreciated from very early time point. If you draw MSO neurons here, they have two dendrites. One's going to the left side, one's going to the right side. And they get numerous synaptic inputs onto each dendrite.

If you make a lesion, so you interrupt the inputs coming from, for example, the right side, all the inputs onto the right dendrites drop off. So it looks like all these inputs are coming from the right side. They've dropped off when their pathway has been cut. And the left ones remain because their pathway is intact.

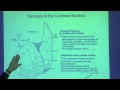
So clearly, the MSO neurons get input from the two sides. Now, way back in the 1940s, a psychologist whose name was Lloyd Jeffress proposed the model for detection of the ITDs. And he guessed at several locations in the brain where this model could actually be present. And one of his guesses was in the MSO.

And it turns out the MSO was the correct of his several guesses. And this is a very interesting model for neural processing of ITDs. And it has several important assumptions.

First, the MSO receives input from the left and the right side, as we have just gone over. So these are axons coming in from the left side. And these are axons coming in from the right side. And the dots there are the MSO neurons themselves.

The dots are very fussy kind of neurons. They don't just respond to any input. They're very discerning. They say, OK, I got some input from the left side. Not a big deal. We get some input from the right side, I'm not going to get excited about that. But I'm going to get very excited if I get input from the left and the right side at the same time. That is, coincidentally.

And so the MSO neurons are sometimes called coincidence detectors. That is, they detect and they respond only when they get coincident input from the left and the right side. Well, how's that going to help us if we're delaying one side versus the other?

Well, the second major component of the Jeffress model is that the axons providing input, which we now know are coming from the cochlear nucleus, they run down the length of the MSO. And as they run down the length, they give off branches to each MSO neuron in this long chain going from left to right.

And if you know anything about spikes that are traveling down axons or nerve fibers, you'll know that the spikes don't get instantly to the very tip of the axon. But it takes them time to travel down the axon.

And so for example in this axon, the impulse is coming down here and it gets to this leftmost branch first. And then a little bit later in time, it gets to the next branch. And so on and so forth until it gets to the rightmost branch at the longest delay.

So Jeffress said, the inputs to the MSO are, if you will, delay lines. That is, axonal impulse propagation takes time. You can set these lines up so that they are delay lines.

The inputs on the right have corresponding delays. Now, how big are the delays? And the flip side of that question is, how long does it take impulses to travel down axons?

So another name for that is the conduction velocity in axons. Well, these are, let's say, myelinated axons of pretty big size, like 5 micrometers. So let's say they're myelinated, a large diameter. 5 micrometers, let's say.

It turns out that such a conduction velocity for those kinds of axons is about 10 meters per second. And Jeffress was sharp enough to know that in the dimensions of the brain, those conduction velocities work out to predict about the right delay for the kinds of interaural time differences that we're talking about for sounds that differ in azimuth. So Jeffress, at the time he was postulating his model in the 1940s, there were good measurements of axonal conduction velocity. And he realized that these delay lines were pretty good for predicting or compensating for the interaural time differences. Now, how does this model work?

Well, I have a little demo of the model, which is a movie. Which I have in a different PowerPoint. And I'm going to show this coincidence model. And I guess I didn't credit the person who made this movie, which is Tom Yin. And he works on the auditory brainstem and he's based at the University of Wisconsin in Madison.

So what this demo will show you is you'll be looking down onto the brainstem. And the MSO on the left side and the right side will be present. The model is set up to demo the MSO on the right side.

There will be a cochlea on the left and a cochlea on the right. The auditory nerve coming into the cochlear nucleus on the left and the auditory nerve coming into the cochlear nucleus on the right. And those two nuclei will be providing inputs to the MSO.

And action potentials, or impulses, along these nerve fibers will be indicated by little highlights-- little yellow lights. And the demonstration will show you what happens to these incoming impulses that converge at the MSO for a sound that's straight ahead. So a sound that's straight ahead will strike the two sides at the same-- will strike the two pathways at the same. And you'll see what happens to the MSO and which neuron in the coincidence detector array lights up.

Then, I think it'll play that same demo in slow motion. Then, the second part of the demo I think has the sound source displaced off to the left side. So the sound wave front will come and strike the left side first and the right side after a delay-- the interaural time difference. And you'll see what happens to the impulses and the MSO neurons with that second sound source position.

So here are the two cochleas, left and right. Here is the MSO. This is the right cochlear nucleus. This is the left cochlear nucleus. This is the MSO we're not talking about. This is the right MSO.

There was a sound wavefront that hit the two sides equally. And it was a little hard to appreciate, but I think this neuron up here in this part of the MSO lit up. This is going to be the same wavefront in slow motion activating the two cochleas at the same time, the two cochlear nuclei at the same time, and coming in to the MSO. This one gets there first because it's on the right side. And the two impulses arrive coincidentally at MSO neuron number 2. And that's the one, because it gets coincident input-- that's the one that fires off.

Here's a second part of the demo where the sound is now located off to the left side. First, it's going to show you in fast motion and then in slow motion.

Left cochlea activates first, right second. And now, the MSO neuron that got coincident input is located down here, neuron number 6 I believe.

Now, it's going to show you that offset sound source in slow motion. Left cochlea gets activated first, right second. Left cochlear nucleus first, right cochlear nucleus second.

Now, the delay lines are set up so that neuron number six in the MSO is the one that responds because it now is the one that gets coincident input. Is that clear?

So what you've set up then in the MSO is an array of neurons where 0 ITD is mapped up here and left leading ITDs are mapped down here. You've mapped interaural time difference to position along the MSO in the brain. And that's the Jeffress model.

So the Jeffress model has been tested experimentally by going in and recording from single MSO neurons. So easy to say and extremely difficult to do in practice. It's not absolutely clear why. It may be that the MSO neurons are small and there are thousands of big inputs coming to them, so that you get what are called big field potentials in your recordings and very small spikes. So the number of studies of actual MSO recordings can probably be listed on the fingers of one hand. So we don't have very much data.

What data we have from MSO neurons shows clearly that the firing rate is dependent on the interaural time difference. And that's what this graph shows here. I'm sorry it's not very clear, but 0 interaural time difference is right here with the dashed line. The firing rate is plotted on the y-axis. These dots over here indicate the firing rate for just left ear sound. Or in the other one, just right ear sound. So there's not a very big firing for presentation of sound in just one ear or the other. That's consistent with the Jeffress model.

Also, consistent with the Jeffress model is that if you get a particular ITD from the particular neuron that you're recording from, that neuron fires a great deal. And other ITDs elicit much less firing. That is, the delay lines didn't allow coincident input to come and excite that neuron. So firing rate that changes a great deal as a function of ITD is consistent with the Jeffress model.

There, probably because there's so few data, the idea of this mapping along the MSO is not borne out by the scanty experimental distance. So we don't really know that there's a map as a function of a particular brain distance. This is the anterior-posterior distance. And they put this line here. Really, the data are all over the map. So it's not clear that there's an organized mapping. It is clear that there's a function of firing when you change the ITD.

So there are some updates to the Jeffress model. And I'm not going to go through these in detail, but I want to point them out to you because this is part of the answer to your assignment. The assignment says, sort of here's the Jeffress model. Give me a quick outline of it. So that's just what I said. I've given you that part.

The second part says, well, the Jeffress model is maybe currently under discussion. What are new experimental evidence-- new I mean from the last 15 years-- that's not perfectly consistent with the Jeffress model?

And you should go to this paper, which is the assigned paper for today's lecture, in which they discuss point number 1, point number 2, and several other points. At least one other point is demonstrated in that paper to show some experimental evidence from MSO recordings which is not perfectly consistent with the Jeffress model. Or makes you think, well, maybe they Jeffress model is not complete, or is outright wrong.

And these are recordings from Brandt et al. The earlier slide I showed you was from recordings in Cat. Cat has become less and less the experimental model. And these are now recordings from smaller animals which are more in vogue to use experimentally.

In this case, it's from the gerbil, which is a popular animal. It has a big MSO, good low-frequency hearing where you use prominent ITD cues. And this paper clearly is a challenge to the Jeffress model. I don't think it completely rules it out, but clearly there are some data from this paper to suggest that it might not be everything.

Now, the second part of the assignment. Actually, that's the second part. The third part of the assignment comes from some other experimental data that I'm not going to give you because you don't need to know about them. But some labeling studies have asked the question, OK, I'm going to inject a neural tracer into my cochlear nucleus neuron. I'm going to trace its axon and I'm going to find this nice, ladder-like delay line in the MSO.

Those labeling studies haven't been particularly gratifying in that they don't fit this model so well. I say here, at first it was thought that there were delay lines from both sides. Labeling studies suggest that there is only a delay line for contralateral input.

OK, so that's not exactly consistent with the Jeffress model. And even more recent studies since I wrote this suggests maybe there aren't even delay lines at all. So experimentally, someone doesn't see a delay line, that doesn't mean it's not there. It just means maybe it's not so obvious. But people have started thinking about maybe there are other ways to provide delays in inputs to the MSO that might make the Jeffress model work. If you have coincident detectors and they respond only when the delay a certain ITD-- matches the ITD. So the third part of the assignment asks you for other ways that you can think of to create delays to MSO neurons.

And let me give you a couple hints to the answers that I'm looking for. I think you should think about the synapse between the input from the cochlear nucleus to the MSO neuron. How could you create different types of delays using synaptic properties? So this is kind of a thought question because these haven't been measured yet.

Secondly, there is another way to create delays. And it comes from properties of the cochlea. And that brings us to our reading for today. We always have a reading.

The reading is from this obscure document, also called our textbook. OK, and the reading is on page 61. Page 61 is the early part of the book. It's talking about the ear, the cochlea. It says, "But you may also note that the vibration of parts of the basilar membrane tuned to frequencies below 1 kilohertz-- very low-- appear time shifted or delayed relative to those tuned above 1 kilohertz. This comes about because of the mechanical filters that make up the basilar membrane. They're not all in phase with each other. If you look at Figure 2.4--"

So everybody should look at Figure 2.4 in the text. So this is my devious way of getting you to actually open the textbook. You will see that the impulse responses of the lower frequency filters rise to the first peak later than those of the higher frequency ones.

OK, so don't just quote the textbook in your answer. Tell me how you could get a delay that would make up for the interaural time difference using this cochlear property that's mentioned in the textbook page 61. And it's illustrated in Figure 2.4 of the textbook. That's another way people are thinking of an alternate to Jeffress delay lines.

And then finally, because last time I thought that it was too easy-- you guys are too smart-- I added something to the assignment. This fits with my son's view-- my son is in high school and he says, teachers love to load on homework. The more, the better. So I added something to make this assignment more challenging. And here's what I added.

And so I think this has now been posted on the website. It doesn't add a great deal of difficulty, but I think it makes it more relevant to our course. I haven't updated this.

OK, well, look on the website, course website. I haven't updated on my computer yet. Look on the course website. The very last part of the assignment, there's one sentence that says, how would a cochlear implant user have trouble using the Jeffress model to localize sounds? Even if the cochlear implant user had a cochlear implant in the left ear and a cochlear implant in the right ear?

And I think this is a fair question. We spent a lot of time on our course talking about cochlear implants. And cochlear implant processing is clearly very different than we, as normal hearers, have the processing on our auditory nerve. So think about that. How would the Jeffress model not be able to be used very well by a cochlear implant user who had implants in the left and right side?

So this is a written assignment. I think before we talked about how long it should be. And I can't remember how-- maybe five pages is plenty. In the very beginning, it talks about the Jeffress model. So give me a quick sketch.

It's due on December 4, which is the day of the lab tour. And you could send them to me by email or you can bring a printed copy to the lab your. Or, you can bring a printed copy to my office, but that's at Mass Eye and Ear where the lab tour is.

And the idea behind having it due then is I can look them over and grade them, and then we can talk about what I thought is the correct answer to this at the review session, which is the class after December 4.