30.7 Expressions for Coefficients of a Power Series

We have for the most part so far discussed what to do when confronted with a series. You can test its convergence, estimate its limit, and try to find the function it represents, if it is a power series.

Another important question is: how can you find the coefficients in a power series expansion of a given function about some expansion point?

We know from our study of Taylor series in Section 10.2 that the coefficient of the j-th term will be the j-th derivative of the function at the expansion point, divided by j factorial.

This is a useful fact, but not always useful enough, in part because it can be cumbersome to calculate or compute the higher derivatives of a complicated function.

Fortunately our standard functions can be defined in the complex plane, and in it we can give an integral representation of the coefficients of a power series, by using the residue theorem.

Suppose we have a function f(z) and wish to expand it in a series about the point z'. We know that the integral of any function around a simple closed path in the complex plane that surrounds an isolated singular point z' (and no other singular point) of f is 2i times its residue at z', and the residue at z' is the coefficient of in the power series expansion of f at the point z'.

We can therefore deduce that the coefficient in the power series expansion of f(z) about z', which is the residue of at z = z', is times the integral of on any simple closed path around z' that does not include any singular point of f

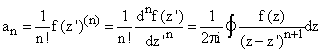
Integrals of this kind can be evaluated numerically for any n without great difficulty.