|
Home | 18.013A | Chapter 12 |
||
|
|
||
How can you do such things?
First put x and j in fixed locations X and Y.
Then set up the following columns on the spreadsheet:
f(xj):
In the first column enter the successive values of f(xj) starting with the first, known value.
For roots you can start with x0 = f(x0) = 1.
Compute later values f(xj) by using the linear approximation tangent line at xj-1 evaluated at argument x, fLxj-1(x) or f(xj-1) + f '(xj-1) (x-xj-1). (xj-1 is the entry in the second column in the previous row.)
xj:
In the second column apply the inverse function, f -1 to the value in the first column.
Once you have entered your instructions for f(x1) and x1, you can copy these down a hundred rows, and you are done.
What happens if f is a root, x1/m?
In general we have
f(xj) = fLxj-1(x) = f(xj-1) + (x - xj-1)f '(xj-1)
For j-th root, ![]() so that this formula reduces to
so that this formula reduces to
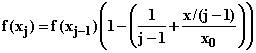
And that is all you need enter. The rest is copying down.
|
|