5.3 Representations of a Line in Two and Three Dimensions

Two points P₁ and P₂ on a line, L, determine L.

L can be described parametrically as the set of points with coordinates those of P₁ + s * (P₂ - P₁) for some number s.

(P₂ - P₁) is a vector which points in the direction of L.

In two dimensions so that the vectors here are 2-vectors, there is only one direction perpendicular to L, and that direction can be obtained by switching the coordinates of (P₂ - P₁)  and changing one sign, (thus (7, -4) is perpendicular to (4, 7)).
With N the perpendicular vector, the equation of the line becomes Nr = NP₁.

We do this out explicitly  L consists of the points obeying

x  = P_1x  + s * (P_2x - P_1x )

y  = P_1y  + s * (P_2y - P_1y )

and the equation for L is

(P_2y - P_1y ) x - (P_2x - P_1x )y = (P_2y - P_1y )P_1x - (P_2x - P_1x )P_1y

which when solved for y is

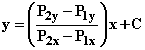for some constant C.

The ratio 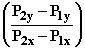, the coefficient of x in the equation for the line, is the difference of y coordinates of the two points divided by the difference in x coordinates. It is called the slope of the line L.

The constant C is called the y-intercept of the line L. It is the value of y on L where L meets the y axis.

In three dimensions, a line is determined by two equations. You can describe it as above parametrically (though now all points and vectors have three components), but you must find two vectors normal to (P₂ - P₁) to find equations that characterize it. You have infinite choice in doing so, but two convenient choices are

i( P₂ - P₁) and j(P₂ - P₁)

and you can require that the dot product of each of these with r (recall r = (x, y, z)) is what it is with P₁. This gives you two equations which together determine the line.

To find a point on a line from equations you fix one coordinate arbitrarily and solve the two equations for the other two coordinates.

The following applet allows you two enter two arbitrary points. It then shows you the line in 3 space that your points determine, and the parametric representation of that line.

Exercises 5.1 Find two equations for the default line in this applet. Then choose two random points, and find two equations for the line they lie on.