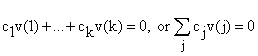3.5 Linear Dependence and Independence

A linear dependency among vectors v(1) to v(k) is an equation, 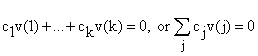in which some of the c's ar not 0. A set of vectors is said to be linearly independent if there is no linear dependence among them, and linearly dependent if there is one or more linear dependence.

Example: suppose v(1) = i + j; v(2) =2i; v(3) = 3j.

Then v(1), v(2) and v(3) are linearly dependent because there is the relation

6v(1) = 3v(2) + 2v(3), or 6v(1) - 3v(2) - 2v(3) = 0

Exercise 3.11 Prove: any k + 1 k-vectors are linearly dependent. (You can do it by using mathematical induction.) (If you are not familiar with mathematical induction read this solution and become familiar with it!) Solution